Apéndice A

Los parámetros teóricos que describen el comportamiento de las ondas internas marcadas con arábigos en la figura 7 fueron calculados mediante la solución numérica de la ecuación (Miropol'sky 2001):

con las condiciones de frontera W (-H) = 0, W (0) = 0 (tapa rígida). Aquí, ω es la frecuencia de la onda interna, f es el parámetro de Coriolis, k_h es el número de onda horizontal y N² es la frecuencia de Brunt-Väisalä. Como las mediciones se realizaron en agua somera (i.e., Hλ, << 1, donde H es la profundidad del lugar y λ la longitud de las ondas internas), para estimar los parámetros de las ondas no lineales se utilizó el modelo no lineal de Korteweg de Vries (ver Miropol'sky 2001):

donde ζ es el desplazamiento vertical, C₀ es la velocidad de fase de la onda lineal, t es el tiempo y x es la coordenada horizontal.

Los parámetros de no linealidad α y dispersión del medio p se calcularon, para el caso de una estratificación continua, mediante la función propia W(z) y la integración numérica de:

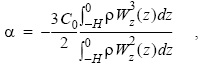
De los valores de α y β, y de las alturas medidas de las ondas ζ₀, se obtuvo la velocidad de fase de los solitones C_s y sus semianchuras o parámetros horizontales característicos L_s, mediante: C_s = C₀ + αζ₀/3 y L_s = {(12β)/(αζ₀)}^1/2 .

Dado que una solución particular de la ecuación A2 es de la forma de un solitón descrito por:

entonces, se determinó que el período τ₀ = 2π/(k_hC₀) corresponde a la duración de la onda, en el nivel sech²(1) = 0.42 de su altura, medida desde el valle (ver página 82 de la monografía de Konyaev y Sabinin 1992).

También se calculó el parámetro de Ursell, que relaciona los parámetros de no linealidad y de dispersión del medio (Miropol'sky 2001):

donde L es la longitud de la onda lineal.