Apéndice A. Algoritmo exacto para inferencia bayesiana

Dentro de los algoritmos de inferencia exacta tenemos el polytree (Pearl, 2000), el clique tree (Lauritzen y Spiegelhalter, 1988) y junction tree (Cowell, 1999). El método de Pearl es uno de los primeros y más utilizados. La propagación de las creencias, de acuerdo con Pearl (2000), siguen el siguiente proceso: sea e el conjunto de valores para todas las variables observadas. Para cualquier variable X, e puede dividirse en dos subconjuntos: ^e-x, el cual representa todas las variables observadas que descienden de X y ^e+x, que representa todas las demás variables observadas. El impacto de las variables observadas sobre las creencias de X pueden representarse a través de los siguientes dos valores:

λ(X) y π(X) son vectores cuyos elementos están asociados a cada valor de X:

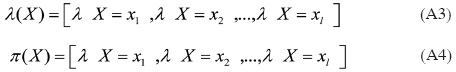
La distribución a posteriori se obtiene usando (A1) y (A2).

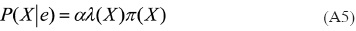
donde α= 1 / P(e) y la multiplicación por pares de los elementos en λ(X) y π(X). Por otro lado, para encontrar las nuevas creencias, se calcula la ecuación (A5). Los valores de λ(X) y π(X) se pasan entre las variables de una manera ordenada. λ(X) y π(X) se calculan de la siguiente manera: λ(X) se calcula utilizando λ(Y₁, Y₂,..., Y_m) donde λ(Y₁, Y₂,..., Y_m) son hijos de X. Primero, cuando X toma el valor x⁰ los elementos del vector λ(X) se asignan de la siguiente manera:

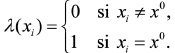
Para el caso donde X no tiene valor, tenemos . Al Utilizar (A1), λ(X) se expande como:

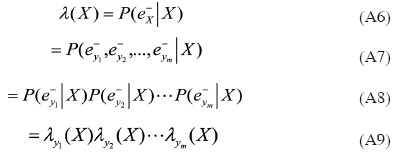
Usando el hecho de e^-_y1 , e^-_y2,...,e^-_ym que son condicionalmente independientes, y definiendo lo siguiente:

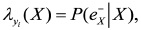
Se tiene que para cada λ_yi (X), el cálculo se realiza de la siguiente manera:

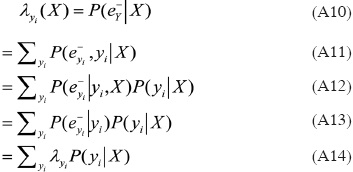
La expresión final muestra que para calcular el valor de λ(X), únicamente se requieren las λ y las probabilidades condicionales de todos los hijos de X. En forma compacta, el vector X(X) se calcula como:

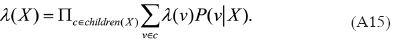
Para el cálculo de π(X) se utiliza el padre Y de las X. En efecto, usando (A2):

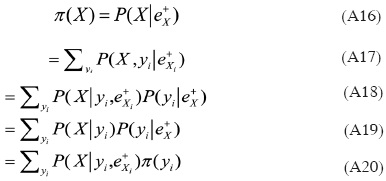
Lo anterior muestra que para calcular π(X), se requieren las π de los padres X, así como sus probabilidades condicionales.

Se pueden presentar problemas con el método de inferencia de Pearl debido a los ciclos que se generan cuando se elimina la direccionalidad (ver Pearl, 1988, capítulo 44). Por tanto, el algoritmo junction tree de Cowell (1999) ha resultado más útil y práctico: convierte la gráfica dirigida en un árbol cuyos nodos son cerrados para proceder a propagar los valores de λ y π a través del árbol; el proceso es el siguiente:

1. Moralizar la red bayesiana, esto significa relacionar por pares a los padres de cada nodo.

2. Triangular la gráfica anterior.

3. Identificar los nodos máximos y completos para construir el árbol, el cual se convertirá en el junction tree.

4. Propagar los valores de λ y π a través del árbol para generar la inferencia, o probabilidades a posteriori.