Appendix I

Proof of Proposition 1

(1) Note that in the first period, a sophisticate has always the option of consuming zero amount of alcohol, in which case he/she would face the same maximization problem as a TC agent in the second period and therefore he/she would choose the same lottery. His/her welfare loss with respect to a TC agent would come from the difference in utility from not consuming alcohol in the first period, which is bounded by . Because the sophisticate has always this option, he/she would never choose a higher amount of alcohol that gives him/her a lower overall utility.

(2) We prove it with an example. Because we assume that the instantaneous utility function is continuous and unbounded, we can find a lottery that pays any payoffs. Suppose that there are two lotteries, lottery one, L₁, that pays a utility of δ(αⁿ) · (3C) / (1 -δ(αⁿ)) + C for sure in the second period and zero in the third period and a second lottery, L₂, that pays a utility zero in the second period and a utility of (3C) / (1 -δ(αⁿ)) for sure in the third period. In the first period, the naif does not realize that his/her consumption of alcohol affects his/her decision in the second period and consumes the amount of alcohol that maximizes his/her instantaneous utility for that period: αⁿ. In the second period, the naif, after consuming αⁿ units of alcohol in the first period chooses lottery Li. The welfare loss for the naif for taking lottery Li instead of L₂ is 2C.

Proof of Proposition 2:

We will show that an individual facing a lottery with benefits in the second period of has an upper bound to their social welfare loss of / —.

An individual with an alcohol discount factor of δ(α) would consume a lottery only if the expected payoff of the lottery is positive: - δ(α) • c > 0. If a lottery has payoffs bounded from above by a constant , the lotteries are accepted only for values of c lower than /δ(α) and the welfare loss for accepting these lotteries is lower than /δ(α). Given that is the lower bound for δ(α), the welfare loss is lower than /δ — .

Proof of Proposition 3:

For the case of a lottery with an expected utility lower than - from the point of view of a TC agent, a partially naïve agent with a perceived discount (a) would limit his/ her consumption of alcohol if he/she believes that he/she will take the lottery if he/she consumes the amount of alcohol that maximizes his/her instantaneous utility in the first period, that is if the expected utility of the lottery with the amount of alcohol aⁿ is greater than zero: 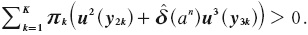For this to happen, it must

be a lottery with present benefits and future costs. Both partially naïve agents consume the amount of alcohol that allows them to avoid this lottery, that is the amount for 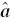the agent that makes 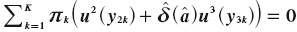and the amount 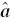´ for the agent ´ that makes 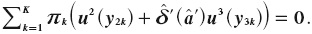This results in their perceived alcohol discount factor of the second period Jbeing the same for both individuals, that is: 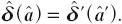Given that 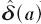and 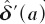are decreasing functions on a, and that 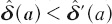for all a, we must have that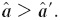

However, given that their true alcohol discount is δ(α), which is lower than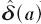 and 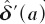for any amount a, and that it is a lottery with present benefits and future costs, he/ she would take the lottery anyway, as the expected utility of the lot tery is greater than zero for both agents 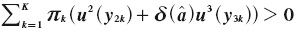and 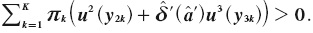Therefore, every partially naïve agent takes the lottery in the second period, even as they limit the amount of alcohol they consume in the first period. Therefore, any difference in welfare for both partially naïve agents is due to their alcohol consumption in the first period.

Because they are limiting their consumption of alcohol with respect to the amount that maximizes their instantaneous utility in the first period, the less they limit their consumption, the better they are. Given that the partially naïve agent with perceived discount 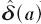is limiting his/her consumption of alcohol less than the partially naïve agent with perceived discount 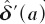he/she must be better off.

Proof of Proposition 4

(1) Let's call (α^TαS,y^TαS,L^TαS) as the optimal amount of alcohol, numeraire and lottery for a sophisticate when there is a tax T_a on alcohol. Note that when there is no tax on alcohol the sophisticate has always the choice of consuming the same amount of alcohol, and the same lottery with a higher amount of the numeraire: (a^TaS,y^TαS + T_α · α, L^TαS). Because the sophisticate has always this option, he/she has a weakly higher utility when there is no tax on alcohol. The sophisticate has always the option of drinking _no alcohol in the first period and because the welfare loss of this option is boundedby , he/she can always choose this option and avoid any welfare loss higher than from a tax on alcohol. _

(2) If U² (0, L) < — , the cost of choosing lottery L is higher than the utility from consuming alcohol, and therefore the sophisticate is going to limit his/her amount of alcohol in the first period if he/she believes he/she will take the lottery if consumes the amount of alcohol that maximizes his/her instantaneous utility in the first period. As any positive tax on future costs weakly reduces the expected utility of L, the individual can increase her consumption of alcohol as the attractiveness of the lottery has been reduced. Given that he/she was consuming less than the amount of alcohol that maximizes his/her instantaneous utility for the first period, he/she would increase his/her consumption of alcohol, increasing his/her utility.

Proof of Proposition 5:

(1) We prove it by showing that a tax on alcohol reduces the welfare in the first period at most in and show that it may increase the welfare of the lottery chosen in the second period, as individuals that consume less alcohol choose lotteries that have a higher utility from the point of view of the TC agents.

First period. A naif consumes the amount of alcohol that maximizes his/her utility in the first period. This amount of alcohol is given by the following first order conditions: u' (αⁿ) = p_α when there is no tax and u' (α^Tαm) = p_α + T_α when there is a tax T_α on the price of alcohol. Because u(α) is a decreasing function on α, αⁿ > α^Tαn.

In the first period, as the tax on alcohol moves the naif from his/her optimal consumption of alcohol, his/her instantaneous utility decreases. However, he/she always has the option of not consuming alcohol and not paying any tax, in which case his/her utility decreases at most in . Because the naif has always this option, he/she cannot do worst than this.

Second period. Now we show that a tax on alcohol weakly increases the welfare from the lottery chosen in the second period.

Let's call X_i as the expected utility of all the payoffs of lottery i paid in the second period (as seen in the second period) and z_i as the expected utility of all the payoffs of lottery i paid in the third period (as seen in the third period). If we call lottery L_α as the lottery chosen by a naif after a consumption of alcohol a in period one, then we have inequality 1: X_α + δ(α)z_α > X_i + δ(α)z_i for any i ∈ . If, after the imposition of tax T_α, the naif consumes the amount of alcohol α^Tαn < αⁿ in the first period and chooses a lottery L_Tαn different than L_α in the second period and we have inequality 2: X_Tαn + δ(α^Tαn)z_Tαn > X_α + δ(α^Tαn)z_α. By adding inequalities 1 and 2 we get that z_Tαn > Z_αand, therefore, we know that δ(α^Tαn))z_Tαn > δ(α^Tαn)z_α. If we add this last inequality to inequality 1, we get that x_Tαn+ z_Tαn > x_α + z_a and therefore the welfare from the lottery chosen when there is a tax on alcohol is weakly higher as compared with the case where there isn't one.

(2) We prove it with an example. Suppose that there is only one lottery, one that pays C · δ(α^Tαn) for sure in the first period and - C for sure in the third period. If αⁿ is positive, then αⁿ > α^Tαn and δ(αⁿ) < δ(α^Tαn). Therefore, he/she would take the lottery if there is no tax on alcohol, but he/she wouldn't take it if there is a tax on alcohol Ta. Therefore the tax gives a naif a welfare gain of C (1 - δ(α^Tαn)). Because this is true for any C > 0 and any tax Ta the welfare gain of a tax on alcohol is not bounded by any constant.