Appendix

The banking decision-making problem and the Brent-Powell algorithm

The decision-making problem for the monopolistic bank is stated as follows:

Subject to

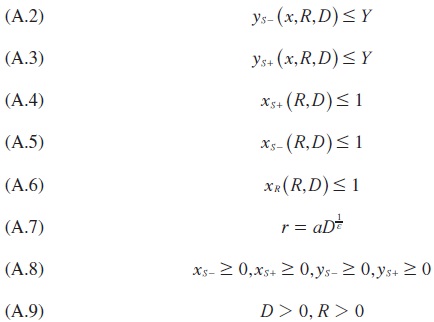
Equation (A.1) is the simplified banking objective function (10) under the assumption that f(x) and g(y) are uniform density functions (Laplace criterion to deal with uncertainties in both sides of the balance sheet). Inequalities (A.2) and (A.3) define the inter-temporal liquidity-solvency relationship and its constraints. Inequalities (a.4) and (A.5) define the viability condition of the asset transformation process. Inequality (A.6) shows the reserves/deposit ratio. Equation (A.7) describes the constant-elasticity supply of deposits. Inequalities in (A.8) define the minimum threshold values for x and y. Inequalities in (A.9) are the non negativity constraints.

Mathematically we solve the above decision-making problem with the Brent-Powell algorithm. The algorithm locates relative minima of functions with more than one variable. It uses a starting point (initial guess) to search for the path of steepest descent of the function to be minimized. Numerically, the algorithm has the advantage that it does not require a differentiable function to estimate the solutions. The idea behind the computational algorithm is to minimize the function by changing the values of the parameter estimates in the direction of a chosen vector. Once a minimum along this vector direction is found, a new vector direction is determined and the function is again minimized in the new direction. By a series of such minimizations, the algorithm iteratively locates the minimum of the objective function. The Brent-Powell algorithm is also known as the "Direction-Set Modification of Powell’s Method". For a detailed mathematical explanation of the algorithm, see Press et al. (1992).