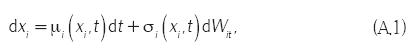
APÉNDICE A

A.1. LEMA DE ITÔ PARA EL CASO DE N MOVIMIENTOS BROWNIANOS GEOMÉTRICOS EN FORMA DIFERENCIAL

Considere la función , f(x,t), X = ( X ₁,X₂,...,X_n), y la siguiente ecuación diferencial estocástica:

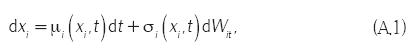
donde dW_it ~ N (0, dt) es un movimiento browniano o proceso de Wiener. Considere también la siguiente tabla de multiplicación para la diferenciación estocástica,

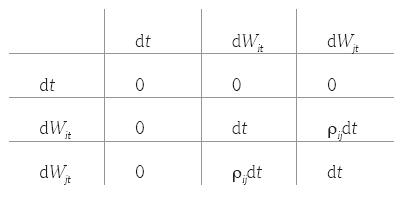
Obsérvese que, en la tabla anterior, el coeficiente de correlación ρ_ii = 1, para todo i = 1,…, n. Para obtener el lema de Itô, primeramente se hace una expansión en serie de Taylor hasta los términos de segundo orden, ya que los términos de orden mayor se anularían según la tabla arriba enunciada. Por lo que se tiene

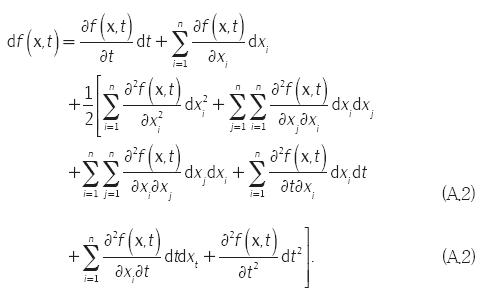
Ahora, se sustituye en la ecuación el movimiento geométrico browniano en su forma diferencial y se hace uso de las reglas de multiplicación para la diferenciación estocástica,

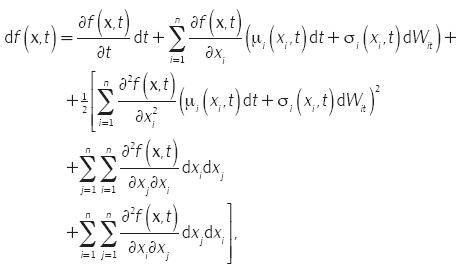
al sustituir

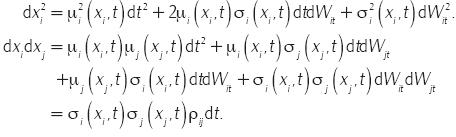
y simplificar, se tiene que

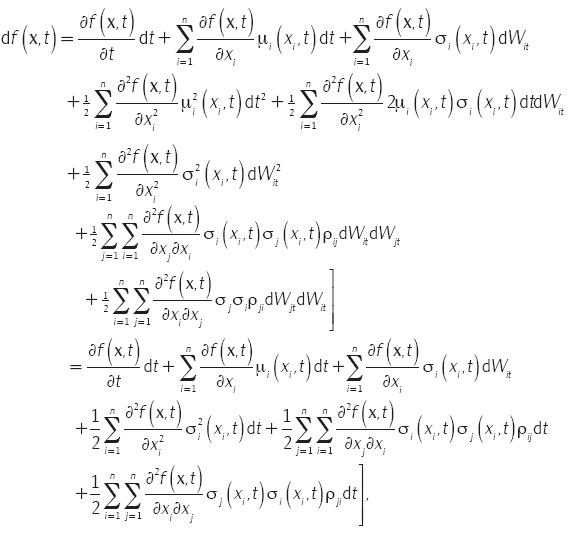
de donde, finalmente, se obtiene

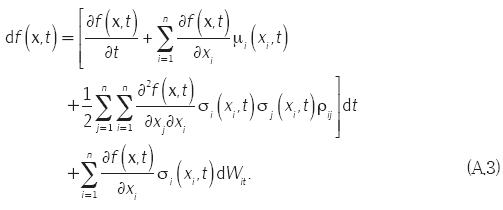
A.2. DEMOSTRACIÓN DEL TEORÉMA DE VERIFICACIÓN PARA PROGRAMACIÓN DINÁMICA

Demostración del teorema 2. Supóngase que H y g son dadas como se enunció anteriormente. Se elije una regla de control arbitraria u ∈ U y un punto fijo (x, t). Se define el proceso X^u en el intervalo de tiempo [t,T] como la solución de la ecuación

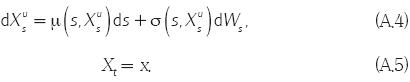
Obsérvese primero que

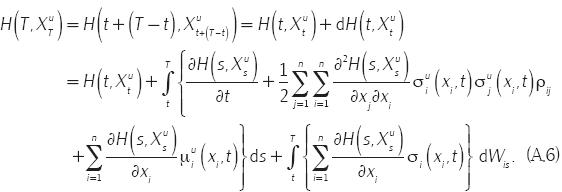
Ahora bien, como H es solución de la EDP HJB, se tiene que

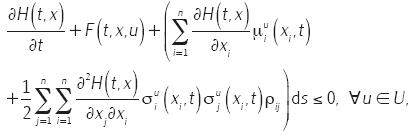
entonces, para cada s, se cumple que

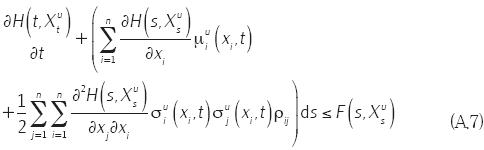
dada la condición de frontera de la EDP HJB y las ecuaciones A.6 y A.7, se sigue que

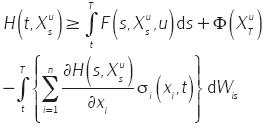
al tomar valor esperado se tiene

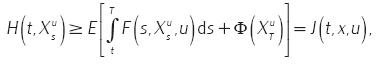
de donde se concluye que

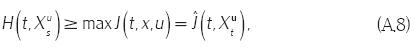
esto toda vez que la regla de control u fue elegida arbitrariamente.

Ahora, suponga que se elige una regla de control u(t, x) = g (t, x), dado por supuesto el inciso iii del teorema 2, de manera análoga se obtiene,

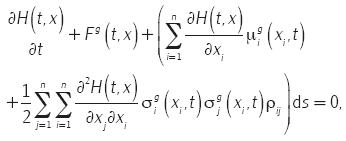
lo que conduce a la siguiente igualdad

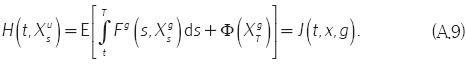
Dado que 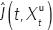es la función de valor óptima, se tiene que

pero al unir las ecuaciones A.8, A.9 y A.10, se sigue

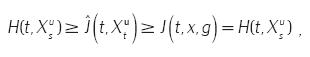
es decir,

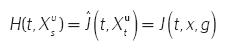
por tanto, H = 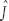y g es la regla de control óptima.