APPENDIX

A.I See Benítez (2009).

A.II Proposition (3.a) and b) from Theorem 1 imply that w > 0 ∀ r ∈ [0, R], this result and (4.a) imply that KS(r)r < 1 and a) follows. According to (4.a), when r increases from 0 to R we have lim_{r→ R} KS(r)r + lim_{r→ R}w(1 + tr) = 1. When r = R the previous equation may be written as K(R)R + lim_{r→ R} w(1 + tr) = 1. As shown in Benítez (2009), lim_{r→ R} w = 0 thus, substituting in the preceding equation yields KS(R)R = 1 implying b). On the other hand, the relation between the cost and the price of production in the complementary sector obeys the relation C_c(r)(1 + r) + l_c = C_c(r) + PN_c where C_c, l_c are respectively the cost of the means of production and the wages paid while PN_c is the difference between the value of production and its cost (net product of the sector). Consequently, C_c(r)r + l_c = PN_c ⇒ [C_c(r)/PN_c]r + l_c /PN_c = 1, an equation that may be written as:

Because l_c /PN_c > 0 ∀ r ∈ [0, R], it follows that KS_c(r)r < 1 ⇒ c). Finally, as l_c/PN_c ≥ 0 when r = R, we have KS_c(R)R ≤ 1 ⇒ d).

A.III I will prove successively that there is a system of type (1) where the capital stock is: a) smaller than T, b) greater than T and c) equal to T.

a) Consider the following system:

Solving the equations, we obtain p₁ = - l₁/[1 - a₁₁ (1 + r)] and p₂ = l₂/ [1 - a₂₂(l + r)] so that p₁/p₂ = (l₁/l₂){[l - a₂₂(1 + r)]/[1 - a₁₁(1 + r)] while KS = [a₁₁ p₁ + a₂₂) p₂] / [(1 - a₁₁)p₁ + (1 - a₂₂) p₂] = [a₁₁ p₁ lp₂ + a₂₂]/[(1 - a₁₁) p₁ / p₂ + (1 - a₂₂)]. Let us choose a₁₁ = 1/ (1 + R) and a₂₂ such that a₂₂ /(1 - a₂₂) = min{T/2, ½(l + R)}. Then, in order for KS to be lesser than T, it suffices to choose l_l and l₂ such that, for the given r, the proportion p_1/p₂ is close enough to zero.

b) Given R, and r ∈ [0, R], let a be such that a = 1/(1+ R) and let 1₀ > 0 be a given quantity of labor. Consider the following spring-like production system:

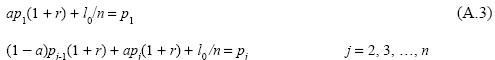
In this system, a units produced by each branch j are employed in its own production and the remaining (1l - a) units in the production of the (j + 1)th branch, except for the nth branch where the corresponding (1 - a) units constitute the net product of the system. Solving for the price of the good produced in each branch yields:

This system permits one to observe that R is determined by the equation 1 - a (1 + R) = 0, implying that a = 1 + R) as initially established. Defining b = (1 - a) (1 + r) / [1 - a (1 + r)] we can write the previous system as:

Substituting p_j-1 for p₁ in the second equation we obtain p₂ = p₁ + bp₁. Then, substituting p_j-1for p₁ + bp₁ in the third equation results in p₃ = p₁ + b[p_l + bp_l], and continuing in this manner, we get p_j. = p₁ + b[p₁ + bp₁ + …+ b ^j-2p₁] for every j > l. Consequently, the preceding system may be written as:

On the other hand, the capital stock in (A.3) is equal to [p₁ + p₂ +…+p_n-1 + ap_n]/(1 - a)p_n, a quotient that may be written in either of the following forms:

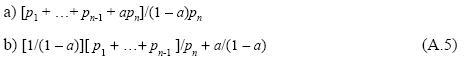
On its turn, by substituting each price except p₁ in the quotient [p₁ + p₂ + …+ p_n-1]/p_n for its equivalent in (A.4) we obtain, after simplifying:

Multiplying the numerator and denominator by (1 - b) results in [(1 - b) + (1 - b²) + (1 - b³) + …+ (1 - b^n-1)]/(1 - bⁿ) = [(n - 1) - (b + b² + b³ + b^n-1)]/(1 - bⁿ) = [(n - 1) - (1 - bⁿ)/(1 - b)]/(1 - bⁿ) = [(n - 1)/(1 - bⁿ) - 1/(1 - b) = 1/(b - 1) - (n - 1) / (bⁿ - 1). Thus, substituting in (A.5.b) yields:

Because b > 1 ∀ r∈[0, R], the quotient (n - 1)/(bⁿ - 1) is a monotonous decreasing function of b whose value tends to zero when n tends to infinity. It is important to note that in this case the capital tends to 1/r. Indeed, lim KS_{n→ ∝} = [1/(1 - a)][1/(b - 1)] + a/(1 - a). Or, b - 1 = (1 - a)(1 + r) /[1 - a(1 + r)] - 1 = {(1 - a) (1 + r) - [1 - a(1 + r)]} / [1 - a(1 + r)] = r/ [1 - a(1 + r)], substituting in the preceding expression yields:

This is the value of KS when all the income corresponds to profits (because (lim KS_{n→ ∝}) r = 1). Therefore, for any T < 1/r, we can choose n great enough in order for the capital of system (A.3) to be greater than T.

c) Consider the production system integrated by the two equations of (A.2), each one of them multiplied by (1 - u) where u e [0, 1] and the n equations of (A.3) each one of them multiplied by u. The capital stock in the aggregated system is determined by:

As this quotient is a continuous function of u, it adopts all the values between those corresponding to the original systems verifying a) and b), so that there is a u verifying c).

A.IV Summing up the two equations of (11) we obtain (λ_A p_h + c_cp_c)(1 + r) + l_I = p_h + p_c and dividing this equation by p_h + p_c results (λ_Ap_h + c_cp_c)(1 + r)/( p_h + p_c) + l_I /(p_h+p_c) = 1 which may be written as c_I(1 + r) + l_I /(p_h + p_c) = 1. Solving each equation of (11) for the corresponding price gives p_h = l_h / [1 - λ_A(1 + r)] and p_c = (l_I - l_h )/ [1 - c_c(1 + r)] substituting the prices in the preceding equation yields c_I (1 + r) + l_I / {l_h /[1 -λ_A(1 + r)] + (l_I - l_h) / [1- c_c(1 + r)]} = 1 permitting one to verify the lemma because the second term from the left-hand side is a monotonous decreasing function of c_c.

A.V We define λ_Aaccording to (15) for the given R, and we choose as the homothetic sector the first equation in system (11). Then, we define l_h and l such that 0 < l_h < l < 1, l₀ = l - l_h and a such that 0 < a <λ_A, the resulting system (A.3) will be the complementary sector. Choosing as sector II the equation (1 -λ_A) p_h(1 + r) + (1 - a)p_n(1 + r) + 1 - l =p_II we have a system respecting the conditions. The capital stock of the complementary sector, measured with the net product of that sector is determined by (A.5). This conclusion and (A.7) imply that lim_{v→ ∝} [c_c /(1 - c_c)] = 1/r, hence (lim_{n→ ∝}c_c)/[1 - (lim_{n→ ∝}c_c)] = 1/r ⇒ (lim_{n→ ∝} c_c)r = 1 - (lim_{n→ ∝} c_c) ⇒ (lim_{n→ ∝} c_c)(1 + r) = 1. From this result and (12), it follows that lim_{n→ ∝} c_I = lim_{n→ ∝} c_c, which together with the equation (lim_{n→ ∝} c_c)(1 + r) = 1 and (7) imply that lim KS_{n→ ∝}= l/lr = 1/r.

A.VI Making m = (T - 1/R)/[1 - Tr ] verifies a). From (18.b), it follows that KS(r) (1 + mr) = m + 1/R so that KS(r) = (m + 1/R)/(1 + mr), multiplying the two sides by r, we conclude that KS(r)r = (mr + r/R)/(1 + mr) < 1 if r < R, so that KS(r) < 1/r ∀ r ∈ [0, R]. Finally, deriving (m + 1/R)/(1 + mr) as a function of m results in [1 + mr - r(m + 1/R)]/(1 + mr)² = (1 - r/R)/(1 + mr)² > 0 ∀ r ∈ [0, R].

A.VII Let T = (1 - F)/r, according to Theorem 2 there is a system such that KS(r) = T. lt follows from (4.a) that in this system we have w(r) = 1 - KSr = 1 - [(1 - F)/r] r = F.

A.VIII Some data of the graphs in Figures 1, 2 and 3.