Anexo
Como se planteó en la sección III, la técnica de análisis discriminante ha sido ampliamente utilizada en estudios que pretenden verificar la precisión en la división de dos grupos de individuos o industrias. En dicha sección se presentaron los resultados más importantes para efectos de nuestro análisis, mientras que en este anexo se exponen algunas pruebas complementarias que permiten consolidar el análisis de robustez que provee el uso de la técnica en cuestión.
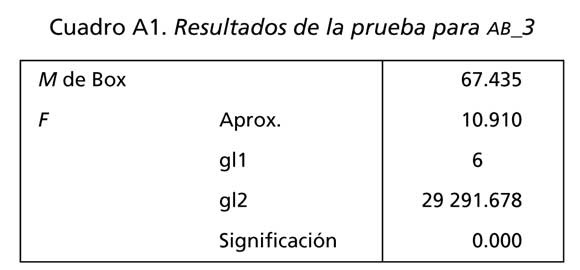
Uno de los supuestos del análisis discriminante es que las matrices de varianzas y covarianzas entre cada grupo son equivalentes. Con el fin de evaluar este supuesto, los cuadros A1 y A2 indican los resultados del estadístico M de Box, el cual tiene como hipótesis nula la igualdad entre matrices de covarianzas poblacionales entre ambos grupos. Los resultados indican que existe una diferencia significativa entre estos grupos. Sin embargo, Burns y Burns (2009) establecen que para muestras grandes un resultado como éste no es tan importante. Por lo tanto, continuamos con el análisis.

Con el fin de expresar una medida del ajuste de la función discriminante, los cuadros A3 y A4 muestran la Λ de Wilks, que indica el porcentaje de varianza no explicada por la función discriminante. De esta manera, el modelo con la clasificación industrial AB_3 explica 38.1% de la varianza de la variable independiente, mientras que el modelo para AB_5, 47.1%. Con el objetivo de conocer la significación estadística de la función discriminante, las últimas casillas de los cuadros A3 y A4 indican que la función es estadísticamente significativa.


Una vez que hemos encontrado evidencia de la significación estadística de la función discriminante, es conveniente considerar el peso de cada una de sus variables independientes en la clasificación de las clases industriales en AT/BT. Para esto, los cuadros A5 y A6 muestran los coeficientes estandarizados de la función discriminante. Estos coeficientes manifiestan evidencia del considerable peso absoluto y relativo que tienen las variables asociadas al gasto en investigación y desarrollo tecnológico en ambos modelos.


Como contraparte, la variable de productividad resultó con el menor peso en los dos modelos. En todas las variantes, su peso cambia del modelo AB_3 al AB_5, lo que podría interpretarse como significación de las variables adicionales en el paso del modelo de tres a cinco variables. Sin embargo, destaca que la orientación de mercado X desplace a IED del segundo lugar en el modelo con cinco variables. Además, el signo positivo en todas las variables indica congruencia en lo planteado a nivel teórico sobre el impacto directo que tendrían estas variables en las capacidades tecnológicas.
Además de los coeficientes estandarizados de la función de discriminante, existen los coeficientes de Pearson como indicador de la importancia relativa de las variables independientes para la ubicación de los individuos de estudio entre los grupos. Estos coeficientes muestran la correlación de cada variable con la función discriminante y se encuentran agrupados en la llamada matriz de estructura en los cuadros A7 y A8.

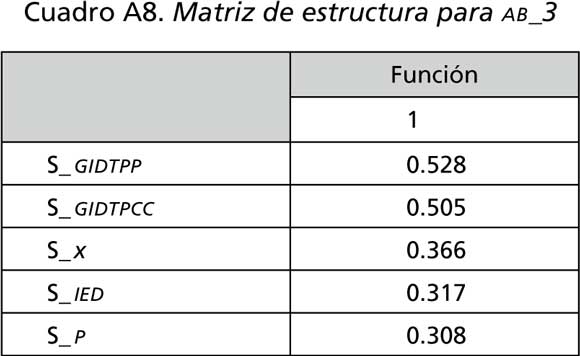
En estos cuadros se refuerzan las conclusiones obtenidas con los coeficientes estandarizados al mostrar los mismos patrones de importancia de las variables.14 Un coeficiente por debajo de 0.30 es considerado comúnmente como una variable no importante, por lo que al estar todos los coeficientes de Pearson por encima de ese nivel, existe evidencia de una importancia significativa de todas las variables para la agrupación de las clases económicas en AT/BT y de que las nuevas variables incorporadas en el paso del ejercicio de tres variables a cinco son apropiadas.
La contribución parcial de cada variable independiente, controlando por el efecto del resto de estas, la obtenemos con los coeficientes sin estandarizar, los cuales se muestran en las ecuaciones de la función discriminante:
 (A1)
(A1)
 (A2)
(A2)
Un indicador que brinda evidencia de una separación de las clases industriales en los grupos AT y BT, con base en la función discriminante, es la comparación de los centroides o medias de los grupos de las variables independientes. En los cuadros A9 y A10 se puede apreciar que los centroides de las clases AT se encuentran relativamente separados del grupo de clases BT y con signos diferentes.


14 Las variables asociadas al gasto en investigación y desarrollo tecnológico ocupan el primer lugar en la determinación de los grupos, la productividad ocupa el último lugar y los pesos disminuyen en el paso de tres a cinco variables.