Apéndice A1
La optimalidad de la estrategia de control basada en E*(t) dada por la ecuación (6.18) y su respuesta x*(t) puede corroborarse utilizando métodos de programación dinámica. Sin embargo siguiendo a Clark y De Pree (1975), es posible dar una justificación directa. Para este fin observemos que la funcional objetivo (6.4) admite la representación equivalente
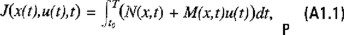
donde
y
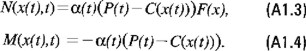
La función C(x(t)) está dada por la ecuación (6.15). La funcional J(x(t),u(t),t) se obtiene a partir de (6.4) eliminando la variable de control E(t) mediante el uso de la ecuación (6.1) considerando ahora como variable de control u(t) a la tasa de crecimiento poblacional. El Hamiltoniano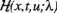 
es en este caso
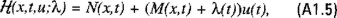
y la correspondiente función de conmutación σu(t) es
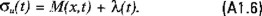
La trayectoria singular se obtiene cuando σ u(t) se anula sobre algún intervalo de tiempo de longitud positiva, por lo tanto en ese intervalo la derivada de σu(t) también se anulará. Obteniendo la derivada de σu(t), utilizando la ecuación adjunta (5.10) y las ecuaciones (6.1), (A1.5) y (A1.6) establecemos
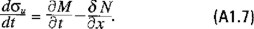
Por lo tanto vemos que para el caso de control singular deberá cumplirse que
Un desarrollo algebraico directo nos permite concluir que la trayectoria singular que se obtiene de la ecuación (A1.8) es exactamente la senda singular xs(t) dada implícitamente por la ecuación (6.14).
De acuerdo con Clark y De Pree (1975), supongamos que las funciones que definen la funcional objetivo (A1.1) nos permiten establecer las desigualdades
Estableceremos a continuación una corroboración directa de la optimalidad de la estrategia de control asociada con x*(t). Sin pérdida de generalidad abordaremos el caso x0<xs(t0). Consideremos la trayectoria x*(t) asociada con la estrategia de control óptimo ilustrada en la Figura 3 mediante la curva ABFQ y sigamos alternativamente la trayectoria xa(t) representada mediante la línea punteada ACDQ.
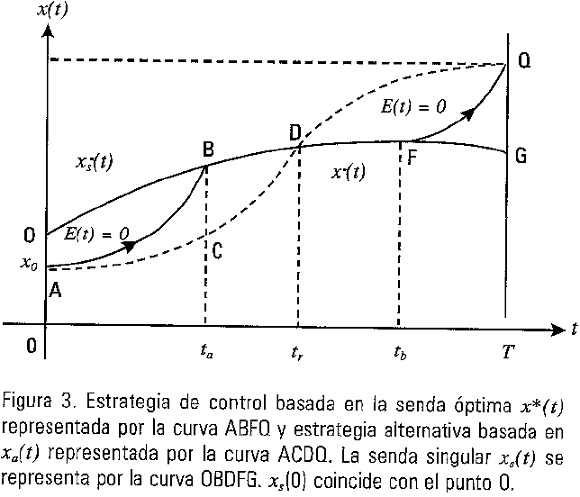
Sea ta el punto a partir del cual se inicia el modo de control singular, tr el punto donde xa(t) intersecta x*(t) y tb el extremo final del intervalo de control singular, entonces para tr se cumplirá la desigualdad
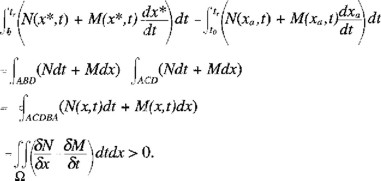
Este resultado se fundamenta mediante la aplicación del teorema de Green considerando que la región Ω delimitada por la curva ACDBA se encuentra acotada superiormente por la senda singular xs(t), y por lo tanto la condición (A1.9) es vigente.
La misma argumentación es válida para el intervalo ta≤t≤T (véase Clark y De Pree, 1975) por lo tanto concluimos que J(x*(t),u*(t),t)>J(xa(t),u*(t),t). Resulta claro que el argumento puede aplicarse a cualquier curva arbitraria xa(t) diferente de x*(t), consecuentemente la senda x*(t) es ciertamente la solución a nuestro problema de control óptimo.
Apéndice A2
En este apéndice ilustraremos el uso de métodos de programación dinámica para establecer la estrategia de control óptimo de la pesquería uniespecífica considerada. Consecuentemente sin pérdida de generalidad abordaremos el caso autónomo de las ecuaciones (6.4) y (6.5) en el cual P(t) y δ(t) permanecen constantes. Así mismo supondremos que es posible aplicar controles de impulso (Clark, 1976, página 48).
Utilizando el principio de optimalidad (véase la ecuación (4.3)), tomando en cuenta la funcional objetivo (6.4) y considerando que el proceso de control se inicia en un tiempo t a partir de un estado inicial x(t), tenemos para la función de valor V(x,t)
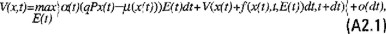
y correspondientemente la ecuación de Bellman (véase la ecuación (4.5)) en este caso será
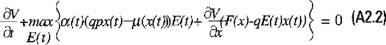
la cual también puede expresarse como
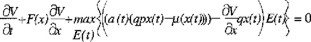
la solución de esta ecuación diferencial parcial puede simplificarse suponiendo V(x,t) que tiene la forma
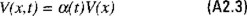
entonces la ecuación de Bellman se transforma en
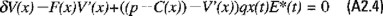
donde C(x) está dado por la ecuación (6.15) y E*(t) se escoge como
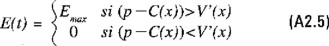
Consideremos ahora la estrategia que mantiene el nivel de biomasa poblacional en un valor constante xs (estrategia de escape constante o de biomasa remanente constante o en equilibrio). La función de valor W(x) (la cual denota el valor presente de los ingresos netos que se obtienen mediante la aplicación de la anterior estrategia con la condición x(t0) = x0) satisface, luego de usar un argumento similar al utilizado en el establecimiento de la ecuación (A2.4)
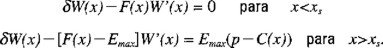
Esto es, en el intervalo (t0,xs), W satisface la ecuación homogénea
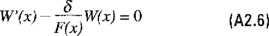
y en el intervalo (xs,∞), la ecuación no homogénea
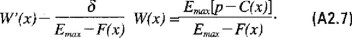
Para x = xs
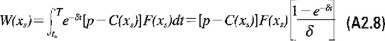
Para determinar explícitamente W(x) las ecuaciones diferenciales (A2.6) y (A2.7) pueden resolverse mediante el uso del resultado de la ecuación (A2.8) como condición de frontera. Esto permite obtener
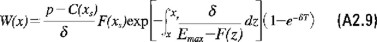
para t0≤x≤xs. Usando el método de variación de parámetros la solución de la ecuación (A2.7) para x>xs vendrá dada por
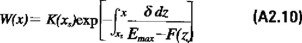
donde
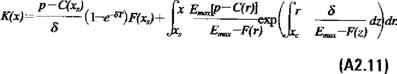
Nótese que cuando Emax→∞ los términos exponenciales en (A2.10) se anulan y
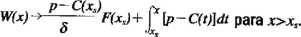
Consideremos a continuación el problema de la obtención del mejor nivel de escape constante. Si dW(x)/dxs = 0 posee solución única para toda x entonces claramente dicha condición lo determinará. Derivando las ecuaciones (A2.9) y (A2.10) con respecto a xs se confirmará que dW(x)/dxs = 0 para toda x, siempre y cuando xs satisfaga
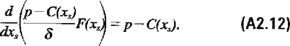
Derivando el lado izquierdo de la ecuación (A2.12) se obtiene la ecuación de la regla aurea (cf. ec. 6.16). Supondremos que las funciones involucradas en dicha ecuación satisfacen las condiciones necesarias de concavidad o convexidad para garantizar la existencia de una solución única x* que determina que el lado izquierdo en (A2.12) sea mayor que el derecho para x<x*, y lo contrario para x>x*. En este caso, x* dada por la ecuación de la regla aurea proveerá el mayor nivel de escape constante.
Solo nos falta demostrar que esta estrategia de escape constante es la mejor de todas las posibles. Para lograrlo demostraremos que la función de valor correspondiente W*(x) satisface la ecuación de Bellman (A2.4). De las ecuaciones (A2.4), (A2.6) y (A2.7) puede verse que éste será el caso siempre que se cumplan las condiciones
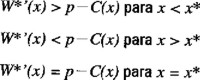
Para establecer el resultado en cuestión notamos primeramente que si x ≠ x* se tiene
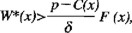
puesto que un nivel de la biomasa remanente constante a nivel x* resulta ser una estrategia mejor que el correspondiente a un nivel x. Entonces de la ecuación (A2.6), para x < x* se tendrá
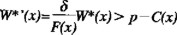
y de la ecuación (A2.7) para x > x*
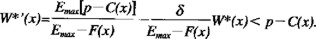
Finalmente, de la ecuación (A2.6) se sigue que
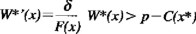
y de la ecuación (A2.7) que
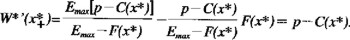
Con esto concluimos la demostración de que W*(x) satisface la ecuación de Bellman. Consecuentemente, la biomasa remanente a nivel x* es la estrategia óptima, y el valor presente de la reserva de capital V(x) es W*(x). Esto es, una expresión explícita para V(x) está dada por las ecuaciones (A2.9) y (A2.10) con xs substituida por x*.