APÉNDICE

Propiedades de la especificación del modelo general probit

El modelo general probit, del cual se estudiarán sus propiedades, es el siguiente:

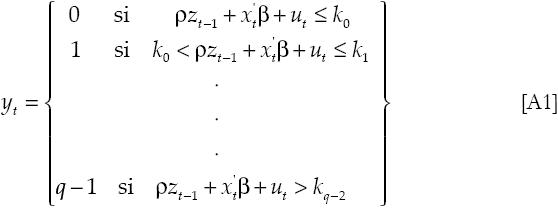
donde z_t-1 = f(y_t-1, y_t-2,..., y_t-n) y el error tiene una distribución normal. Sea el verdadero vector un parámetro denotado por: θ₀ = (β₀', ρ₀)', donde β₀ ∈ℜ¹ y ρ₀ ∈ℜ. Sea el espacio del parámetro denotado por: Θ con θ = (β', ρ)'∈Θ. Para escribir la función condicional de verosimilitud en forma concisa, sea:

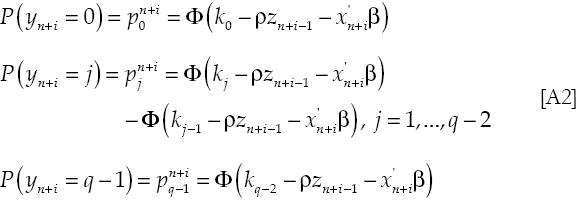
La función de verosimilitud condicional sobre (y₁, y₂,..., y_n), está dada por:

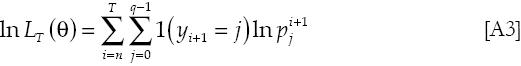
El estimador de máxima verosimilitud es el valor de θ que maximiza [A3]. Nosotros usamos la siguiente notación: ||x|| denota la norma Euclideana de x ∈ ℜ¹; → _p señala convergencia en probabilidad, y → _d denota convergencia en distribución. Para la consistencia de se requieren los siguientes supuestos:

Supuesto A

1) x_t es una secuencia estrictamente estacionaria, variables aleatorias mezcladas fuertemente, donde x ∈ℜ¹ para l ≥ 0 y (E||x||²) < ∞. La distribución de w_t = (x_t', y₁, y₂,..., y_t-n)' no está contenida en algún subespacio lineal de ℜ¹.

2) u_t| x_t, y_t-1, y_t-2 ,..., ∼ iid N(0,1).

3) y_t está dado por [A1].

4) θ₀ es un elemento del interior de Θ, el cual es un conjunto convexo.

Teorema 1: Conforme al supuesto A, → _p θ₀. Para normalidad asintótica, nosotros necesitamos un supuesto adicional.

Supuesto B

1) u_t | (x_t,y₁), (x_t-1, y_t-2),... ∼ iid N(0,1).

Teorema 2: Conforme al supuesto A y B, T^1/2 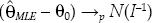, donde I es la matriz de información dada por: I = E (∂/∂θ)(∂/∂θ')ln L_T(θ).