Anexo metodológico

El método se basa en un viejo principio demográfico: la población de edad x al tiempo t es igual a los nacimientos ocurridos en t-x más la historia de mortalidad y migración de la cohorte. Así, el incremento en la población de cierta edad en dos momentos en el tiempo es igual a la suma de las diferencias de los nacimientos y las historias de mortalidad y migración de las dos cohortes. Horiuchi (1988) presentó originalmente el resultado, aquí se reconstruye su formulación, utilizando algunos resultados de Horiuchi y Preston (1988).

Sea μ(x) la tasa instantánea de mortalidad (fuerza de mortalidad) a la edad x. Es bien conocido que la proporción de supervivencia del nacimiento a la edad a en la cohorte de la tabla de vida está dada por:

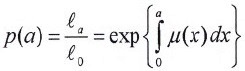
donde 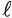_a son los sobrevivientes a la edad a de 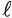₀ nacimientos. De manera análoga, para la cohorte real nacida en t-a, en ausencia de migraciones, la proporción es:

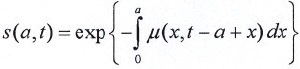
donde ahora μ(x,t) es la tasa instantánea de mortalidad (fuerzademortalidad) a la edad x al tiempo t. El signo negativo en la exponencial del lado derecho se debe a que la tasa es positiva y la mortalidad reduce la cohorte. Para agregar el efecto de la migración internacional utilizamos la tasa instantánea migración neta, cuyo valor es positivo si hay ganancia neta o negativo si hay pérdida neta, así, esta tasa se suma en la exponencial del lado derecho:

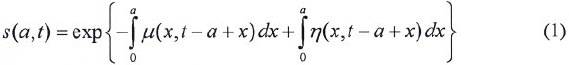
Sea ahora P(a,t) la densidad anual de población de edad exacta a al tiempo t y B(t-a) la densidad anual de nacimientos al momento t-a, claramente:

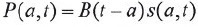
Similar a la tasa de mortalidad, la tasa instantánea de crecimiento es la derivada del logaritmo natural de la población, es decir,

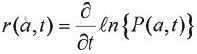
entonces:

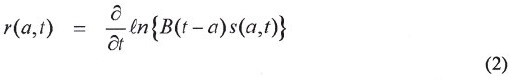
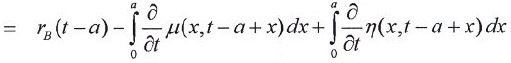
donde r(a,t) es la tasa de crecimiento de la población de edad a al tiempo t, r_B(t-a) es la tasa de crecimiento de los nacimientos al tiempo t.

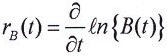
y por (1) la derivada del logaritmo natural de s(a,t) con respecto al tiempo es:

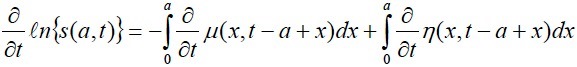
Si multiplicamos ambos lados de (2) para la población al momento t, tenemos el aumento absoluto de la población de edad a:

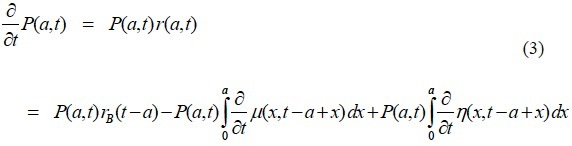
Se puede reconocer la contribución del cambio de la natalidad en el primer término del lado derecho de la segunda igualdad, la mejora de la mortalidad entre las cohortes en el segundo término y la participación del cambio de la migración neta en el tercero.

La versión discreta de la ecuación (3) es:

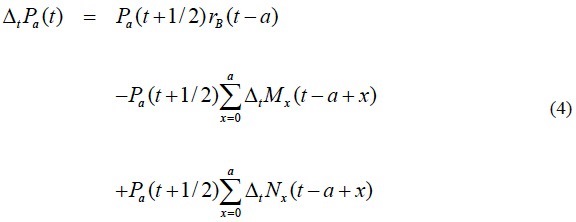
donde P_a(t) es la población de edad cumplida a al tiempo t, M_x (t) y N_x (t) son las tasas de mortalidad y migración neta, respectivamente, de edad cumplida x en el año que empieza en t y r_B (t) es la tasa de crecimiento de los nacimientos:

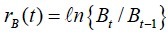
con B_t el número de nacimientos ocurridos en el año que inicia en t.