ANEXO 3
A continuación se presentan formalmente los modelos de regresión multinivel especificados en este artículo. Dado que en el nivel 3 (entidades) no se introdujeron variables, y para fines de simplicidad en la exposición, se muestra únicamente un modelo de dos niveles (individuos y escuelas).
El modelo final especificado para cada asignatura se resume como:
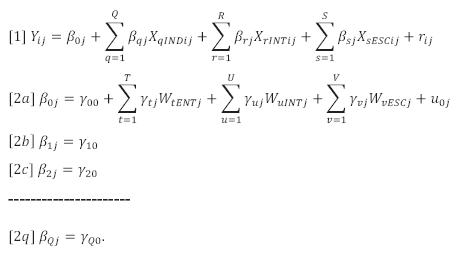
En este modelo:
Yij es el puntaje obtenido en la prueba por el alumno i en la escuela j.
Boj es el puntaje promedio obtenido por la escuela j.
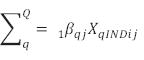 representa la suma de coeficientes para variables "del individuo" (XrINDij), en el nivel individual.
representa la suma de coeficientes para variables "del individuo" (XrINDij), en el nivel individual.
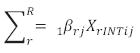 representa la suma de coeficientes para variables "de interfaz" (XrINTij) en el nivel individual.
representa la suma de coeficientes para variables "de interfaz" (XrINTij) en el nivel individual.
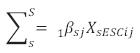 representa la suma de coeficientes para variables "de la escuela" (XsESCij), en el nivel individual.
representa la suma de coeficientes para variables "de la escuela" (XsESCij), en el nivel individual.
γoo es el puntaje global de la prueba a nivel nacional o "gran media".
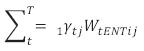 representa la suma de coeficientes para variables "del entorno" (WtENTj), en el nivel escolar.
representa la suma de coeficientes para variables "del entorno" (WtENTj), en el nivel escolar.
 representa la suma de coeficientes para variables "de interfaz" (WuINTj ), en el nivel escolar.
representa la suma de coeficientes para variables "de interfaz" (WuINTj ), en el nivel escolar.
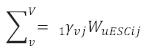 representa la suma de coeficientes para variables "de la escuela" (WvESCj ), en el nivel escolar.
representa la suma de coeficientes para variables "de la escuela" (WvESCj ), en el nivel escolar.
rij es el término de error o efecto "aleatorio" del alumno i en la escuela j.
uij es el término de error o efecto "aleatorio" de la escuela j.
Los sub-modelos βqj = γq 0 indican que las pendientes de los factores individuales sobre los aprendizajes en cada escuela se establecieron como fijos (promedios ponderados a nivel nacional), sin dejarse variar libremente entre escuelas —y obviamente, sin modelarse estas variaciones—.
La explicada por estos modelos se estima, a nivel individual y escolar respectivamente, a través de:

donde 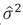 y
y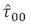 representan, respectivamente, los componentes de varianza de nivel individual y escolar para cada modelo.
representan, respectivamente, los componentes de varianza de nivel individual y escolar para cada modelo.
Para estimar la proporción de varianza explicada específicamente por cada grupo de factores, en el nivel individual se varió el orden de introducción de estos grupos sobre la base de un procedimiento del tipo:
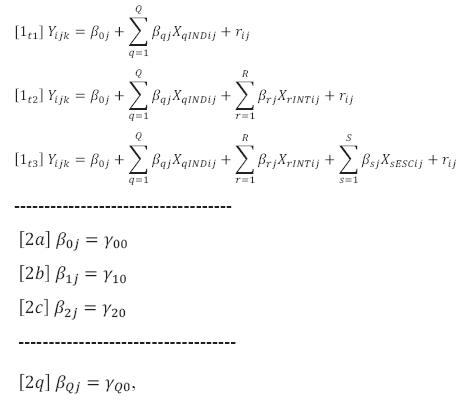
Es decir, se introdujeron los grupos de factores individuales en un orden determinado (tn), siendo el porcentaje de varianza explicado únicamente por el último grupo el que se considera como su efecto específico. El orden de introducción de los grupos se varió de tres maneras, para dejar en último lugar siempre un grupo distinto. Por ejemplo, la proporción de varianza de Y ij explicada específicamente por las variablesXsESCse calculó como la diferencia entre la proporción de varianza explicada por el modelo completo y la proporción de varianza explicada por un modelo sin dicho grupo:

El mismo procedimiento fue seguido para cada grupo de variables. La diferencia entre la varianza explicada por la suma de componentes "específicos" y la varianza explicada por el modelo completo se consideró como varianza explicada por interacciones.
En el nivel escolar se siguió un procedimiento similar al anterior, variando el orden de introducción de los grupos en cada ocasión. El procedimiento base de la estimación fue:
