Anexo

A.1 Formación de las categorías de empleo

Se inició separando a la Población Económicamente Activa (PEA) ocupada y desocupada y la Población No Económicamente Activa (PNEA). Para ello, se echó mano de la variable recodificada clase2 de la ENE-ENOE, cuyas categorías son:

1. Población ocupada.
2. Población desocupada.
3. Disponibles.
4. No disponibles.

Los códigos 3 y 4 corresponden a los no activos. De la población ocupada se retuvieron sólo quienes se desempeñan en el sector no agrícola, es decir, el código 2 de la variable recodificada ambito1.

Para desagregar a la PEA ocupada en formal e informal, se utilizó una combinación de micronegocios, goce de seguridad social y práctica contable. En realidad, se configuró el conjunto del empleo formal y se tomó al resto de la PEA ocupada como informal. Primero fue identificado el tamaño del establecimiento siguiendo la propuesta de Tokman (2004: 181): formal con seis o más trabajadores e informal con cinco o menos. Y después se incorporó el criterio de la práctica contable: si los gastos de la empresa se separan de los gastos de los hogares, se considera que el establecimiento es parte del sector formal; en caso contrario, lo es del informal.

Una vez separada la PEA ocupada del resto de la población, se utilizaron el trabajo principal y el tamaño del establecimiento de ambas encuestas. En la ENE de 2000-2001 se integró el empleo formal con las preguntas p3a, p3b, p3e, p4, p7d_4 y p7d_5 de la manera siguiente:

1. Patrones en establecimientos con seis trabajadores o más (P3a = 1 y p3b = 3, 4, 5, 6, 7, 8).

2. Trabajadores por cuenta propia profesionales o técnicos (P3a = 2 y p4 = 1100-1299).

3. Trabajador a destajo, comisión o porcentaje con seguridad social (P3a = 3 y p7d_4 = 1 o p7d_5 = 1).

4. Asalariado en establecimientos con seis trabajadores o más (P3a = 4 y p3e = 3, 4, 5, 6, 7, 8).

5. Miembro de una cooperativa con seis trabajadores o más (P3a = 5 y p3e = 3, 4, 5, 6, 7, 8).

Y para la ENOE 2010-2011 con las preguntas p3a, p3b, p3d, p6_1, p6_2, p6_4, p6_5 y p6_6, y las recodificadas p3g_tot y segsoc:

1. Patrones en establecimientos con seis trabajadores o más (p3a = 2 o p3b = 1 y p3d = 1 y p3g_tot ≥ 6).

2. Trabajadores por cuenta propia profesionales o técnicos (p3a = 2 o p3b = 1 y p3d ≠ 1).

3. Trabajador a destajo, comisión o porcentaje con seguridad social (p6_1 = 1 o p6_2 = 2 o p6_4 = 4 o p6_5 = 5 o p6_6 = 6 y segsoc = 1, 2, 3).

4. Asalariado en establecimientos con seis trabajadores o más (p3a ≠ 2 o p3b ≠ 1 y p3q ≥ 3).

Finalmente, para incorporar la práctica contable y su reporte a la autoridad hacendaria, tanto en la ENE como en la ENOE, se retiraron del empleo formal, clasificado según los criterios de arriba, a quienes en la variable recodificada tue2 se les asignó el código 5 (sector informal de acuerdo con INEGI, 2014). Asimismo, se consideraron como informales a quienes se dedican al trabajo doméstico remunerado (tue2 = 6).¹

A.2 Metodología

Partida (1996) ofrece una descripción detallada de la tabla de vida activa, de donde se extraen las esperanzas de vida activa y una discusión de sus supuestos inherentes. Aquí, sólo se presentan las ecuaciones necesarias para el cálculo de las esperanzas de vida activa y de su cambio en el tiempo.

Se considera a la población desagregada en las cuatro categorías y se asigna uno a los ocupados formales, dos a los ocupados informales, tres a los desocupados y cuatro a los no económicamente activos.

Generalmente, es mediante las tasas de eventualidad que se transfiere la evidencia empírica al modelo de tabla de vida. Las tasas de movilidad entre las cuatro situaciones observadas se obtuvieron de partir de la información de la ENE-ENOE. Se consideran dos visitas a una vivienda apartadas un año en el tiempo. Se denota por ₅O^ij_x a quienes, estando en la situación i en la primera visita en el intervalo semiabierto de edades exactas [x, x + 5] o de edades cumplidas de x a x + 4, se encontraban en el estado j un año después, con x = 15, 20, 25, ..., 85. Por ejemplo, ₅O¹²₂₅ son aquellas personas ocupadas en el sector formal (sobreíndice 1) de edades 25-29 años en un trimestre y en el sector informal (2) cuatro trimestres después, o bien, ₅O⁴³₂₅ quienes siendo no económicamente activos (4) pasaron a ser desocupados (3) un año más tarde.² El total que se encuentra en la situación i al inicio del periodo anual es:

y en j al final

Una tasa en Demografía se define como el cociente que resulta de dividir los eventos ocurridos en un intervalo de tiempo entre los años-persona vividos por la población durante el mismo periodo, y expresa el promedio anual per cápita de eventos experimentados por la población expuesta.

El cálculo de los años-persona vividos, generalmente se hace mediante modelos de crecimiento, siendo común el aritmético. Si ₅Kⁱ_x son los años-persona vividos en el estado i en el intervalo de edades cumplidas de x a x + 4 al cabo del año de acuerdo con el modelo de crecimiento aritmético, el tiempo vivido es:

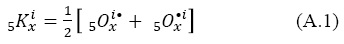
y, de definición, la tasa de movilidad de i hacia j, ₅M^ij_x en el año es:

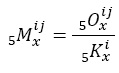
Se denota por 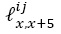a los supervivientes en una tabla de vida que se encontraban en el estado i a la edad exacta x y en j a la edad x + 5 y sea ₅P^ij_x la probabilidad que una persona de edad exacta x en la situación i tiene de sobrevivir a la edad en el estado j. La matriz de supervivientes se define como:

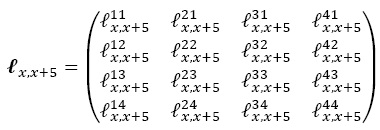
y la de probabilidades:

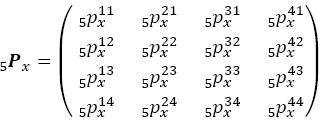
Un individuo no puede estar en dos estados disjuntos al mismo tiempo (la edad exacta x) con lo cual,

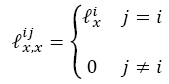
y la matriz de supervivientes para la edad exacta x es:

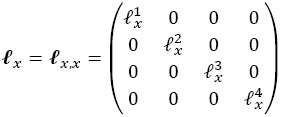
La siguiente igualdad matricial se cumple (Willekens et al., 1982:134):

Para N intervalos quinquenales contiguos, la matriz de probabilidades de supervivencia de la edad x a la edad x + 5N es:

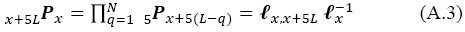
Se denota por ₅^ixP^kj_u a los años-persona vividos en la situación j entre las edades u y u + 5 por quienes estuvieron en k a la edad u y previamente en i a la edad x, ubicados en una matriz como:

Sean ^ixT^j_u los años-persona vividos en la situación j a partir de la edad u para los supervivientes en i a la edad x, colocados en una matriz como:

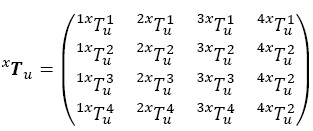
De estos dos últimos conceptos se puede establecer:

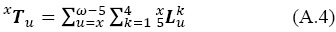
donde el índice de la sumatoria se incrementa de cinco en cinco y ω es límite de la vida humana, esto es, una edad extrema avanzada a la cual nadie sobrevive y se toma tal que ω - u sea múltiplo de cinco.

Sea e^ij_x la esperanza de vida en j para un presente en i a la edad x, decir, los años que espera pasar, en promedio, en el resto de su vida en j una persona que está en i a la edad x. Definida la matriz como:

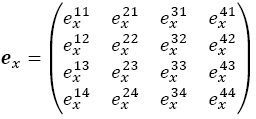
se satisface la siguiente ecuación (Willekens et al., 1982: 138):

Se denota por ₅e^ij_x a la esperanza de vida temporaria entre las edades x y x + 5, es decir, los años que espera pasar, en promedio, en los siguientes cinco años en j un individuo en i a la edad x.

Se acomodan esas esperanzas temporarias en una matriz como:

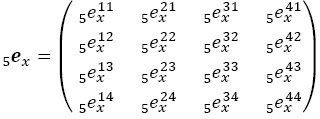
y el tiempo vivido:

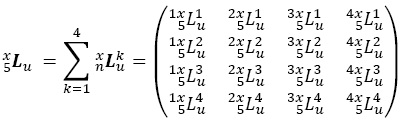
donde ₅^ixL^j_u son años-persona vividos en j entre las edades u y u + 5, por los presentes en i a la edad x ≤ u, independientemente de su situación a la edad u. Por semejanza con (A.5) la siguiente operación matricial se cumple:

Las esperanzas de vida total se pueden obtener como (Partida, 1996: 219):

El objetivo es identificar la contribución de las distintas situaciones y para diferentes rangos de edad, al cambio en las esperanzas de vida activa totales a través del tiempo. Para empezar, se fija una edad inicial del intervalo etario de interés:α ≥ 15 y se designa con el sobreíndice 1 al año 2000 y con 2 a 2010. De acuerdo con (A.7), las esperanzas totales a la edad α son:

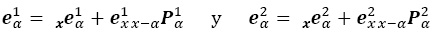
de donde la contribución hasta la edad x a la diferencia en las esperanzas de vida es:

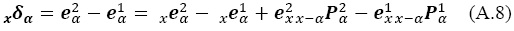
Como el interés se centra en la contribución del intervalo genérico entre las edades x y x + 5, se puede simplificar el procedimiento al tomar la media aritmética de las condiciones posteriores a ese grupo etario, es decir,

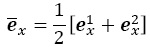
con lo cual se puede escribir (A.8) como:

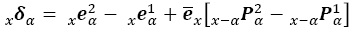
para la edad x + 5

y la contribución del intervalo quinquenal:

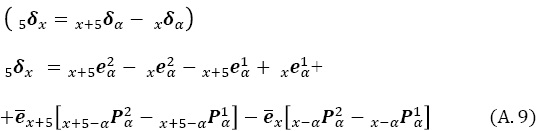
Al multiplicar ambos lados en (A.6) por la derecha, por la inversa de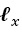

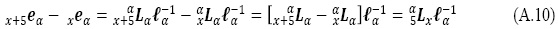
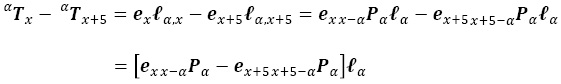
Por (A.5) y (A.2) se tiene:

y por (A.4):

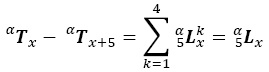
Al igualar:

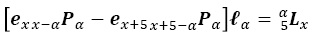
y multiplicar por la derecha por la inversa de 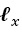ambos lados e introducir (A.10):

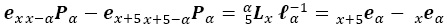
Si se reemplaza este resultado en (A.9):

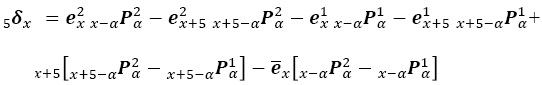
Finalmente, al cambiar por sus componentes y agrupar términos:

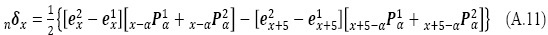
que es la generalización al caso de estados múltiples de la propuesta de Andrevv et al. (2002: 4) para tablas de vida simple.

Como se ha supuesto que la mortalidad es igual para toda la población, sea _em_x la tasa de mortalidad común y la matriz de tasas definida como:

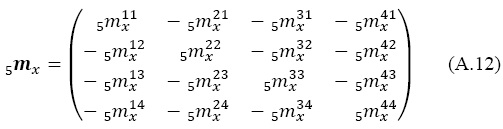
donde los elementos de la diagonal principal son (Rogers y Ledent, 1976: 287):

Se puede ver que la suma de cada una de las cuatro columnas de la matriz ₅m_x es igual a la tasa de mortalidad, con lo cual queda asegurado que el monto de la cohorte de la tabla sólo se modifica por efecto de la mortalidad, pero no por la movilidad entre las cuatro situaciones.

Nour y Suchindran (1984: 327) llegaron a la siguiente fórmula bajo el criterio de crecimiento exponencial:

La exponencial de una matriz se obtiene mediante la extensión de la conocida expansión en serie de potencias para escalares (Gantmacher, 1959: 113):

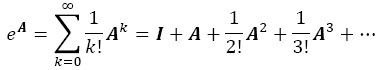
Si se arreglan los términos de la ecuación (14) de Willekens et al. (1979: 135) y se introduce (A.6) se tiene:

Una vez obtenidas las tasas de la ENE para 2000 y de la ENOE para 2010, mediante (A.14) se tienen las probabilidades de transición con (A.3) las matrices de probabilidades acumuladas
_{x - α}P_α y _{x + 5 - α}P_α con (A.15) las esperanzas de vida temporarias y, finalmente, con (A.11) es posible valorar la contribución de cada grupo etario al cambio temporal en las esperanzas de vida total.

Ausencia de mortalidad

Al proceder de esta manera y omitir la tasa de mortalidad en (A.13), por la definición de ₅mⁱⁱ_x todas las columnas de la matriz de tasas en (A.12) suman cero y su determinante es igual a cero, con lo cual la matriz de tasas no tiene inversa y no es posible valorar las esperanzas de vida temporarias con (A.15).

Dado el supuesto de igual mortalidad, la suma de cualquiera de las columnas de la matriz de tasas temporarias es igual a la esperanza de vida temporaria total, ₅e_x. Ante la ausencia de mortalidad, cada uno de los presentes al inicio del intervalo etario vivirá cinco años, de donde, para retirar el riesgo de fallecer, se proporcionan las esperanzas de vida temporarias como:

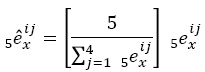
donde el símbolo "^" indica la ausencia de mortalidad. De esa manera se evita el inconveniente matemático de la inexistencia de la inversa de la matriz de tasas.

No obstante, para la aplicación de (A.3) y, por ende, de (A.11), se usa la matriz de tasas sin mortalidad al valorar ₅P_x con (A.14), de tal suerte que todas las columnas de cualquier matriz _{x - α}P_α o _{x + 5 - α}P_α suman uno, es decir, supervivencia total o ausencia de mortalidad. En todos los casos se supone que la esperanza de vida a los 90 años es cero:

e^ij₉₀ = 0 para toda i, j = 1,2,3,4

Las tasas de mortalidad usadas provienen de la reconstrucción demográfica de la Sociedad Mexicana de Demografía (SOMEDE 2011).

Notas

¹ Las variables clase2, ambito1, tue2 y segsoc se incluyen en las bases de micro datos del cuestionario socioeconómico.

² Se compara el segundo trimestre de 2000 con el segundo de 2001 y el primero de 2010 con el primero de 2011.