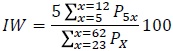
Anexo metodológico
Índice de Whipple: este índice puede medir la atracción de cualquier dígito o de dos a la vez. Para edades terminadas entre 0 y 5 se empleó la ecuación siguiente:
Donde Px es la población a la edad x.
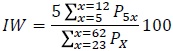
El supuesto básico del índice es que la población correcta varía en forma lineal dentro de los grupos de edades 23-27, 28-32, 33-37,...,58-52.
Índice de Myers
Este índice se define a partir de la suma de los valores absolutos de los índices individuales para cada dígito Mj con j = 0, 1, 2, ..., 8, 9, los que estiman la atracción de rechazo de cada uno de los dígitos en la declaración de edad.
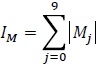
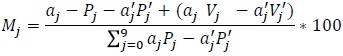
Donde
aj = j + 1 para j: 0,...,9
a'j = 9 ñ 1 para j: 0,...,9
Pj = ∑ i ≥ 1 P10i + j Número de personas que han declarado edad cumplida terminada en el dígito j y dentro de la población de diez años y más cumplidos.
P'j = ∑ i ≥1 P10i + j Número de personas que han declarado edad cumplida terminada e n el dígito j y dentro de la población de veinte años y más cumplidos.
Vj = ∑ i ≥1 V10i + j Número real de individuos con edad cumplida terminada en el dígito j dentro de la población de diez años y más cumplidos.
V'j = ∑ i ≥1 V10i + j Número real de individuos con edad cumplida terminada en el dígito j dentro de la población de veinte años y más cumplidos.
Rangos para clasificar la concentración en cuanto a la preferencia de dígitos: 0 y 5, bajo; entre 5.1 y 15, intermedio; entre 15.1 y 30, alto; y entre 30.1 y más, muy alto.
Índice de Naciones Unidas: INU = 3 * RS + PDCH + PDCM
Donde RS es el índice de regularidad de sexos y PDCH y PDCM representan los promedios de desviaciones respecto a 100, de las poblaciones masculina y femenina respectivamente.
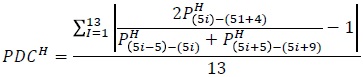
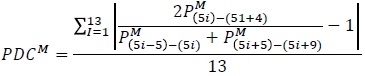
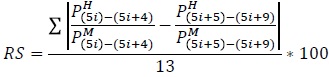
Debido a que el indicador no tiene límites precisos su interpretación se basa en la experiencia, para lo cual se establece que índices mayores de 40 indican información deficiente, entre 20 y 40 de calidad intermedia y menores a 20 satisfactoria.
Los valores de ambos censos fueron calculados con los datos de la muestra no ponderada.