Anexos

ANEXOS

1. Estimación del modelo⁶

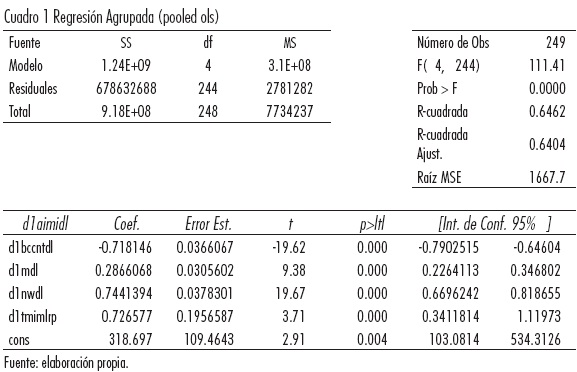
1.1.1 Regresión agrupada (Pooled M. C. O.)

El enfoque más simple para analizar datos de panel es omitir las dimensiones del espacio y el tiempo de los datos agrupados y sólo calcular la regresión MCO usual. Este modelo se expresa como:

Y_it = α + β₁X_1it + e_it                 (i)

Donde i significa la i-ésima unidad transversal (países) y t el tiempo t (meses).

La regresión agrupada toma la información como un todo sin discriminar los datos temporales o transversales. Esta estimación es útil para dilucidar patrones preliminares, los signos y las magnitudes de las variables independientes.

Al examinar los datos de la regresión agrupada se puede ver que todos los coeficientes son individual y estadísticamente significativos, vemos que los coeficientes tienen los signos que se esperaban, y que el valor R² = 0.6462 es razonablemente alto.

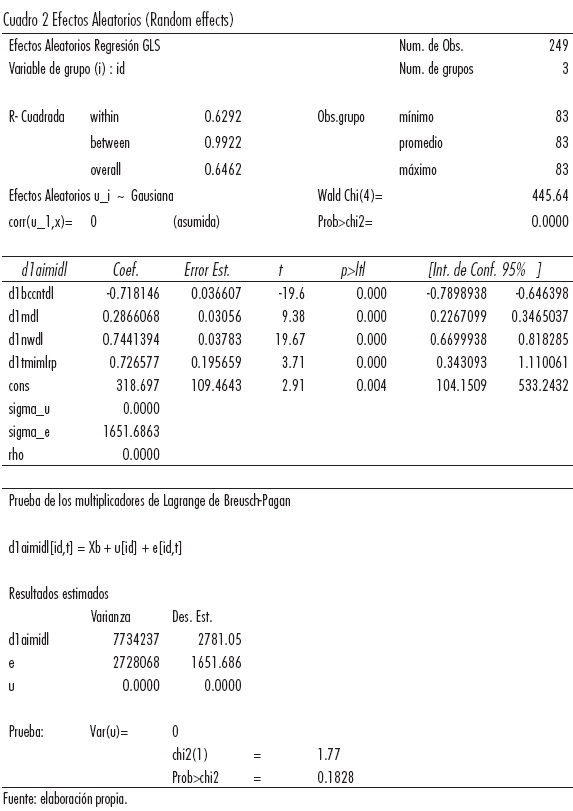
1.1.2 Efectos aleatorios (Random Effects)

La ecuación (i) supone que el intercepto de la regresión es el mismo para todas las unidades transversales. Sin embargo, es muy probable que necesitemos controlar el carácter "individual" de cada país. El modelo de efectos aleatorios permite suponer que cada unidad transversal tiene un intercepto diferente. Este modelo se expresa como:

Y_it = α_i + β₁X_1it + e_it                 (ii)

Donde α_i = α + u_i . Es decir, en vez de considerar a α como fija, suponemos que es una variable aleatoria con un valor medio α y una desviación aleatoria u_i de este valor medio. Sustituyendo α_i = α + u_i en (ii) obtenemos:

Y_it = α + β₁X_1it + u_i + e_it                 (iii)

Si analizamos la ecuación (iii), observamos que si la varianza de u_i es igual a cero, es decir σ²_u = 0, entonces no existe ninguna diferencia relevante entre (i) y (iii). Para saber cuál de los dos modelos es mejor, ya sea efectos aleatorios o el de datos agrupados, aplicamos la prueba de Breusch y Pagan conocida como "Prueba del Multiplicador de Lagrange para Efectos Aleatorios". La hipótesis nula de esta prueba es que σ²_u = 0. La prueba se rechaza, si existe diferencia entre (i) y (iii), y es preferible usar el método de efectos aleatorios.

El valor "p" nos muestra que no podemos rechazar la hipótesis nula Ho, por lo que es preferible usar el método de la Regresión Agrupada (POOLED M.C.O.).

Sin embrago, se requiere considerar el carácter "individual" de cada unidad de datos transversales (países); por lo tanto se procedió a especificar un modelo de Efectos Fijos para comparar cuál modelo resulta ser el óptimo.

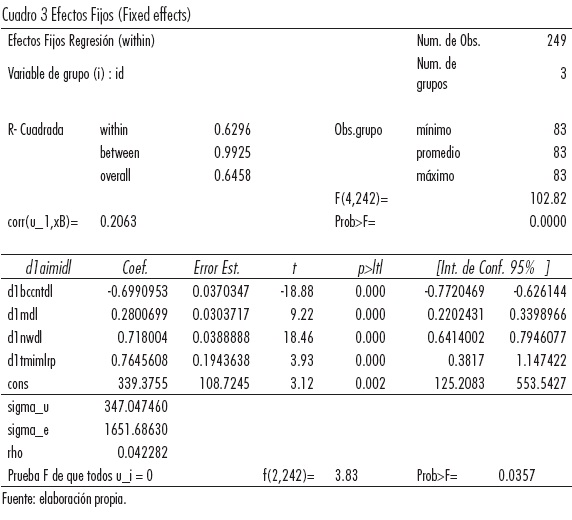
1.1.3 Efectos fijos (Fixed Effects)

Otra manera de modelar el carácter "individual" de cada país es a través del modelo de efectos fijos. Este modelo no supone que las diferencias entre los países sean aleatorias, sino constantes o "fijas", y por ello debemos estimar cada intercepto Ui. Para que el intercepto varíe con respecto a cada país utilizamos la técnica de "las variables dicotómicas de intersección diferencial" (utilizar variables dicotómicas conduce al mismo resultado que si restamos a cada observación la media de cada país), que se expresa de la siguiente manera:

Y_it = v_i + β₁X_1it + e_it                 (iv)

Donde v_i es un vector de variables dicotómicas para cada país.

Para saber cuál de los dos modelos es mejor, utilizamos una prueba "F" restrictiva, también conocida como la prueba de Chow en la que RSS_R es la suma de cuadrados de residuos que se obtiene de la estimación M.C.O. en el modelo agrupado y RSS_U es la suma de cuadrados de los residuos de la estimación por mínimos cuadrados de las variables dicótomas.

Para probar la Hipótesis:

Ho = v₁ = v₂ =........= v_i = 0.

H₁ = v₁ ≠ v₂ ≠........≠ v_i ≠ 0.

Calcular:

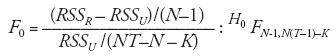
Si F > F_a (N-1, NT-N-K), rechazar Ho; de lo contrario, no se rechace, donde F_∞(N-1) y F_a (NT-N-K) y (N-1) son los grados de libertad del numerador y del denominador, respectivamente, y α es el nivel de significancia. Alternativamente, si el valor p-value del F obtenido de la ecuación es suficientemente bajo, se puede rechazar Ho.

En relación con el modelo (iv), el modelo (i) asume un intercepto común para todos los países (es decir, no incluye variables dicotómicas por país). Como ya se vio la hipótesis nula es que v₁ = v₂ = ... = v_i = 0 (o sea, que todas las variables dicotómicas por país son iguales a cero). Si la prueba se rechaza, significa que al menos algunas variables dicotómicas sí pertenecen al modelo, y por lo tanto es necesario utilizar el método de efectos fijos.

El valor "p" nos indica que podemos rechazar la Ho, por lo que es preferible usar el método efectos fijos al modelo agrupado (pooled).

Como podemos observar, ya no es necesaria la prueba Hausman para determinar si el modelo es de efectos fijos o es de efectos aleatorios, ya que queda demostrado que el modelo óptimo es el de efectos fijos.

1. 1.4 Pruebas de autocorrelation y heteroscedasticidad

Autocorrelación

Es importante señalar que aun cuando hemos modelado la heterogeneidad temporal y espacial en nuestro modelo, se debe cumplir con ciertas especificaciones. De acuerdo con los supuestos de Gauss-Markov, los estimadores de M.C.O. son los Mejores Estimadores Lineales e Insesgados (MELI) siempre y cuando los errores e_it sean independientes entre sí y se distribuyan idénticamente con varianza constante σ².

Actualmente hay muchas maneras de diagnosticar problemas de autocorrelación. Wooldridge desarrolló un método en el cual se establece que la hipótesis nula de esta prueba es que no existe autocorrelación, naturalmente, si se rechaza, podemos concluir que ésta sí existe (Wooldridge, 2002).

El valor "p" nos indica que No se puede rechazar la hipótesis nula Ho, por lo que no tenemos problema de Autocorrelación de primer orden.

Correlación contemporánea

Las estimaciones en datos panel pueden tener problemas de correlación contemporánea si las observaciones de ciertas unidades están correlacionadas con las observaciones de otras unidades en el mismo periodo. En la prueba de Breusch y Pagan para identificar problemas de correlación contemporánea en los residuales de un modelo de efectos fijos. La hipótesis nula es que existe "independencia transversal" (cross-sectional independence), es decir, que los errores entre las unidades son independientes entre sí.

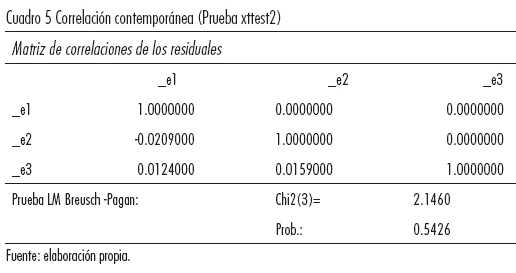
El valor "p" del estadístico X² indica que no podemos rechazar la Ho, por lo tanto no existe problema de correlación contemporánea.

Heteroscedasticidad

Cuando la varianza de los errores de cada unidad transversal no es constante, nos encontramos con una violación de los supuestos Gauss-Markov. Una forma de saber si nuestra estimación tiene problemas de heteroscedastidad es a través de la prueba del Multiplicador de Lagrange de Breusch y Pagan. Sin embargo, de acuerdo con Greene (2000), ésta y otras pruebas son sensibles al supuesto sobre la normalidad de los errores; afortunadamente, la prueba Modificada de Wald para Heterocedasticidad funciona aun cuando dicho supuesto es violado. La hipótesis nula de esta prueba es que no existe problema de heteroscedasticidad, es decir, σ²_i = σ² para toda i=1.. N, donde N es el número de unidades transversales ("países" en nuestro ejemplo). Naturalmente, cuando la Ho se rechaza, tenemos un problema de heteroscedasticidad.

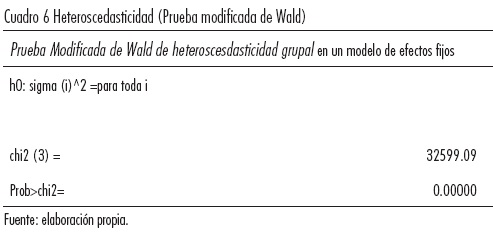
La prueba nos indica que rechazamos la Ho de varianza constante y aceptamos la Ha de Heteroscedasticidad.

Corrección de Heteroscedasticidad

El problema de heteroscedasticidad puede solucionarse con estimadores robustos, con Mínimos Cuadrados Generalizados Factibles (FGLS), o bien con Errores Estándar Corregidos para Panel (PCSE). Beck y Katz (2001) demostraron que los errores estándar de PCSE son más precisos que los de FGLS. Desde entonces muchos trabajos en la disciplina han utilizado pcse en sus estimaciones para datos de panel.

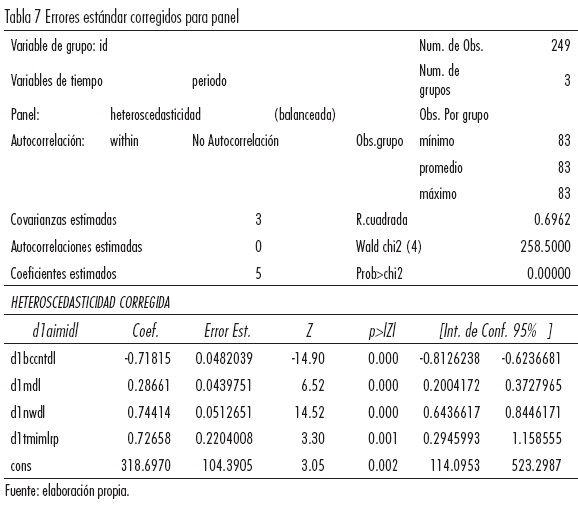
Podemos ver que los coeficientes tienen los signos esperados además de que son estadísticamente significativos. Lo anterior nos muestra el modelo de acumulación de reservas óptimo para datos de panel, el valor "p" de la variable constante sigue teniendo una t poco significativa aunque mejoró con respecto a la regresión de efectos fijos.

Nota

⁶ Las series de tiempo del modelo se pueden localizar en: http://revistas.unam.mx/index.php/pde