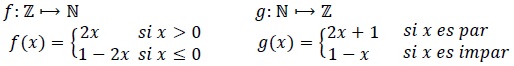
a) Asumiendo que ƒ ea biyectiva, halla ƒ-1 .
b) ¿Es g una función inyectiva? ¿Suprayectiva? ¿Biyectiva? Justifica.
c) Determina g ° ƒ y ƒ ° g dando sus dominios, sus contuadominioo y sus rorpectivas reglas de correspondencia.
Anexos
Prueba Profesor "A"
1. Dada la siguiente relación en ℝ.
R = {(x,y) ∈ ℝ2 / xy = 1}
a) Determina el dominio , la tmagen y el contradominio dn la relación R.
b) ¿Es R una función de ℝ en ℝ? Justifica tu re spuesta.
2. Dada la siguiente relación en ℤ.
R = {(x,y) ∈ ℤ2/ x + y es impar}.
¿Es R reflexiva? ¿Simétrica? ¿Transitiva? Justifica tus respuestas.
3. Sea A = ℝ — {0} Definam os la siguiente relación en A:
R = {(x,y) ∈ A2 / xy > 0}.
a) Demuestra que R es una relación de equivalenc ia.
b) Halla [—1], [1] y el conjunto cociente A/R.
4. Dadas las siguiente funciones:
a) Asumiendo que ƒ ea biyectiva, halla ƒ-1 .
b) ¿Es g una función inyectiva? ¿Suprayectiva? ¿Biyectiva? Justifica.
c) Determina g ° ƒ y ƒ ° g dando sus dominios, sus contuadominioo y sus rorpectivas reglas de correspondencia.
5. Demuestra que ℕ y ℤ- tienen la misma cardinalidad, es decir que #ℕ = #ℤ-.
6. Ejercicio optativo. Sea ƒ : A → B una función suprayectiva.
Si g: B → C y h : B → C son aos funciones tales que g ° ƒ = h ° ƒ, entonces g = h.
Reactivo omitido en el análisis por su carácter optativo.
Prueba Profesor "B"
1. Demuestra AX (B ∪ C) = (AXB) ∪ (AXC).
2. Escribe (por extensión cuando sea preciso) el dominio, el contradominio y la imagen de la siguiente relación entre ℤ y ℝ :
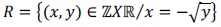
3. Di si es o no R (reflexiva), S (simétrica), T (transitiva) en cada una de las siguientes relaciones en ℝ:
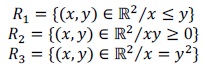
4. Demuestre que R = {(a,b) ∈ ℤ2 / |a| = |b|} es una relación de equivalencia en ℤ.
5. Considera la relación de equivalence en ℝ dada por
R = {(x,y) ∈ ℝ2 /
=
} Encuentra la clase de equivalencia die 3.5.
6. Considera la relación en ℤ:
R = {(x,y) ∈ ℝ2 / y = x2}
¿Es R función de ℤ en ℤ?
7. Para cada una de las siguientes fundones escribe si es o no inyectiva, suprayectiva, invertible:
8. Sean ƒ ℤ → ℤ
Encontrar (muestra el procedimiento) ƒ ° g.
