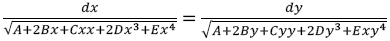
ⁱ Hinc itaque concludimus huius aequationis differentialis :

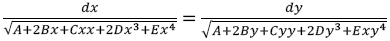
aequationem integralem eamque completam ese

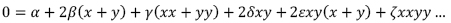
ⁱⁱ Si binae variabiles x et y ita a se invicem pendeant, vt. sit:

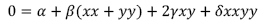
erit sive summa, sive differentia, harum formularum integralium

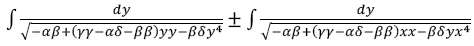
aequalis quantitati constanti.

ⁱⁱⁱ Ces équations sont comprises dans la formule suivante:

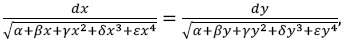
dont l’integrale est exprimée en général par l’équation

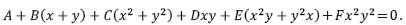
^iv l’equazione differenziale prende la forma

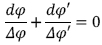
il cui integrale trascendente è secondo le notazioni de Legendre

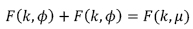
rappresentando con μ il valore di Φ per Φ' = 0 . L’ampliezza μ si otterrà dalla relazione con le precedenti sostituzioni per la fórmula:

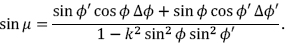
^v CHAPITRE PREMIER
Idée générale des différentes sortes de transcendantes contenues dans la formule intégrale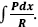

1. Nous représentons par P une fonction rationnelle quelconque de x, et par R le radical

^vi 15. Cela posé, les fonctions ou transcendantes elliptiques comprises dans la formule H, seront divisés en trois espèces:

La première et la plus simple est représentée par la formule ∫ dΦ/Δ;
La seconde es l’arc d’ellipse, compté depuis le petit axe, et dont l’expression est E = ∫ ∆dΦ;
En fin, la troisième espèce est représentée par la formule. . . . . . . . ∫ dΦ/((1 + n sin²Φ)∆) ellecontient, outre le module c commun aux deux autres espèces, un paramètre n qui peut être à volonté positif ou négatif, réel ou imaginaire.

^vii Le problème de la résolution des équations des degrés supérieurs au quatrième est un de ceux dont on n’a pas encore pu venir à bout, quoique d’ailleurs rien n’en démontre l’impossibilité.

^viii 89. Nous supposerons, comme dans la Section précédente, que l’équation proposée soit représentée généralement par

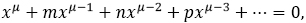
et que ses racines, qui doivent être au nombre de μ, soient désignées par x', x'', x''', x^IV, ··· , x^(μ).
Ainsi l’on aura, par la nature des équations,

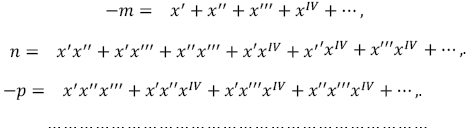
Et il est clair que ces fonctions de x', x'', x''', x^IV, ··· , par lesquelles sont exprimées les quantités m, n, p, ··· seront nécessairement toutes de la forme ƒ[(x', x'', x''', x^IV, ··· )] et que par conséquent ces fonctions seront toutes semblables, ce qui est une propriété fondamentale des équations.

^ix THEOREM 9. Every symmetric polynomial P over F in x₁, x₂, ···, x_n can be written as a polynomial Q over F in the elementary symmetric functions. If P has all integral coefficients, then so too does Q. The degree of Q is less than or equal to the degree of P.

^x Ceterum principia theoriae, quam exponere aggredimur, multo latius patent, quam hic extenduntur. Namque non solum ad functiones circulares, sed pari successu ad multas alias functiones transscendentes applicari possunt, e. g. ad eas quae ab integrali 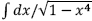pendent, praetereaque etiam ad varia congruentiarum genera : sed quoniam de illis f u nctionibus transscendentibus amplum opus peculiare paramus, . . .

^xi ... Donc, pour embrasser dans la même définition les intégrales prises entre des limites réelles, et les intégrales prises entre des limites imaginaires, il convient de représenter par la notation

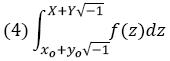
le limite ou l’une des limites vers lesquelles converge la somme. . . Pour obtenir deux suites de cette espèce, il suffit de supposer

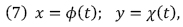
Φ(t), χ(t) étant deux fonctions continues d’une nouvelle variable t, toujours croissantes ou décroissantes depuis t=t_o jusqu’à t=T, et assujetties à vérifier les conditions

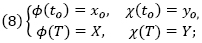
 ... On aura donc

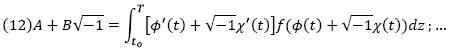
^xii « On peut diviser la circonférence entière de la lemniscate en m parties égales par la règle et le compas seuls, si m est de la forme 2ⁿ ou 2ⁿ + 1, ce dernier nombre étant en même temps premier; ou bien si m est un produit de plusieurs nombres de ces deux formes. »
Ce théorème est, comme on le voit, précisément le même que celui de M. Gauss, relativement au circle.

^xiii E for mulis praecedentibus, quae et ipsae tamquam fundamentales in analysi f unctionum ellipticarum considerari debent, elucet:

a) functiones ellipticas argumenti imaginarii iv, moduli k, transformari posse in alias realis v, móduli Unde generaliter functiones ellipticas argumenti imaginarii u + iv , moduli k, componere licet e functionibus ellipticis argumenti u, móduli k, et aliis argumenti u, móduli k'.

b) functiones ellipticas duplici gaudere periodo, altera reali, altera imaginaria, siquidem modulus k est realis. Utraque fit imaginaria, ubi modulus et ipse est imaginarius. Quod principium duplicis periodi nuncupabimus. E quo, cum universam, quae fingi potest, amplectatur periodicitatem analy ticam, elucet functiones ellípticas non aliis adnumerari debere transcendentibus, quae quibusdam gaudent elegantis, fortasse pluribus illas aut maioribus, sed speciem quandam iis inesse perfecti et absoluti.