Apéndice A

Se consideran los modos no amortiguados del sistema con dos grados de libertad mostrado en la Figura 1. Supongamos que vibra libremente en un modo X_j , y definamos α_j como la relación entre la energía cinética impartida a la masa superior y la energía cinética de la masa inferior, tal que:

Definamos de manera similar β_j como la relación entre la energía elástica almacenada en el resorte superior y la energía elástica almacenada en el resorte inferior durante la vibración libre, tal que:

Si las componentes correspondientes a la masa inferior se normalizan como la unidad, de las dos ecuaciones anteriores podemos deducir los siguientes vectores modales:

o alternativamente

En vista de que los modos son ortogonales con respecto a las matrices de masa y rigidez, las relaciones energéticas cumplen con las ecuaciones siguientes:

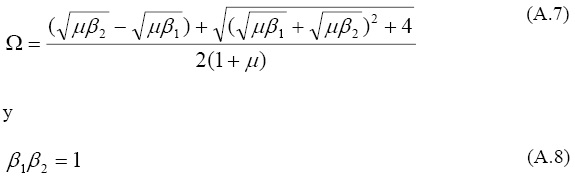
De las ecuaciones A.3 y A.4, se nota que las relaciones energéticas están relacionadas entre si de la siguiente manera:

Para sistemas conservadores, la máxima energía cinética modal E_K es igual a la máxima energía elástica modal E_S, y por tanto en términos de las energías de las componentes superiores e inferiores podemos escribir para el javo modo:

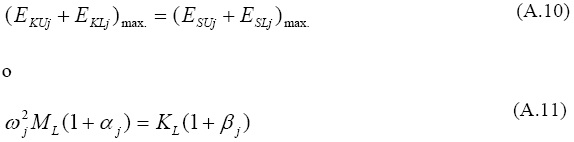
Así pues, obtenemos las frecuencias modales de la expresión siguiente:

Se puede demostrar que las frecuencias modales cumplen con las siguientes expresiones:

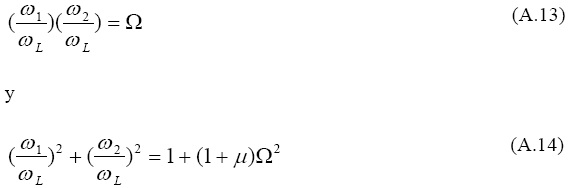
Los factores de participación modal se pueden escribir como:

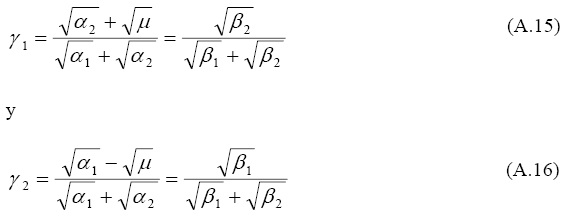
Igualando la disipación de energía modal a la suma de las energías disipadas por cada una de las dos componentes, se puede demostrar que una aproximación de primer orden del amortiguamiento modal viene dada por la siguiente expresión:

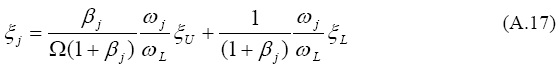
Miranda (2005), demostró que los términos fuera de la diagonal de la matriz de amortiguamiento en coordenadas modales son idénticamente cero si se cumple la siguiente relación:

Si tal fuera el caso, los vectores modales arriba derivados son capaces de desacoplar las ecuaciones del movimiento del sistema con dos grados de libertad que está bajo consideración. Es pertinente ahora discutir la aproximación alcanzada en la derivación del amortiguamiento modal. Con este propósito usamos un procedimiento propuesto por Adhikari y Woodhouse (2001), quienes a su vez se basaron en la obra de Rayleigh (1877). La ecuación homogénea de movimiento para el sistema que se estudia es:

donde M es la matriz de masa, C la de amortiguamiento, y K la de rigidez. El vector y(t) provee los desplazamientos relativos. Se busca una solución armónica de la forma y(t)=Z exp[λt], donde Z es un modo complejo, y λ es una frecuencia natural compleja del sistema. La substitución de y(t) en la ecuación A-19 para el javo modo, resulta en:

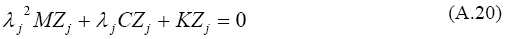
Siempre que las frecuencias y modos complejos estén "suficientemente cercanos" de las frecuencias y modos no amortiguados, un análisis de perturbación de primer orden se puede usar de manera a expresar:

Reemplazando (A.21) en (A.20), y premultiplicando por la transpuesta de X_k , tenemos:

donde M_kl, C_kl, y K_kl son los términos de las matrices generalizadas de masa, amortiguamiento, y rigidez respectivamente. De A.24 para k=j, tomando en consideración la ortogonalidad de los modos no amortiguados con respecto a las matrices de masa y rigidez, e ignorando términos de segundo orden asociados con los elementos fuera de la diagonal de la matriz de amortiguamiento, tenemos:

Dividiendo por M_jj, y suponiendo que:

obtenemos:

lo que conduce a

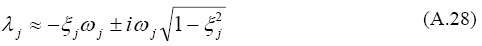
Puesto que el lado derecho de la ecuación A-28 provee las frecuencias complejas exactas, se verifica entonces que la ecuación A.26 constituye una buena selección para expresar el amortiguamiento modal ya que conduce a una aproximación de primer orden de los valores exactos de las frecuencias. Para el caso en que k≠j en A.24, y reteniendo solamente los términos de primer orden, tenemos:

Por tanto, de (A.21) podemos escribir:

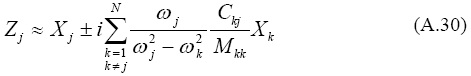
Se observa que, con una aproximación de primer orden, la parte real de los modos complejos es la misma que los modos no amortiguados, y que los términos fuera de la diagonal de la matriz de amortiguamiento generalizada son los responsables por las partes imaginarias. Para el sistema con dos grados de libertad que nos ocupa, después de las substituciones adecuadas tenemos:

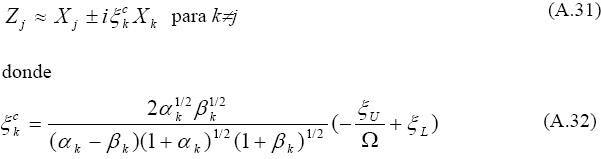
Vemos entonces, que si las propiedades del sistema son tales que la ecuación A-18 se cumple, la parte imaginaria de los vectores modales desaparece. La semejanza entre la ecuación A-32 y la A-17 es aparente. Por lo tanto, esta ecuación puede ser interpretada como el coeficiente de amortiguamiento acoplado para el javo modo, el cual dependiendo de los valores de ξ_U y ξ_L puede ser positivo o negativo. La ecuación A-32 indica que a menos que el amortiguamiento y la sintonía no difieran apreciablemente de la ecuación A-18, el uso de los modos complejos se requiere para el cálculo de la respuesta de los sistemas mecánicos bajo consideración. No obstante, las ecuaciones A-17 y A-28 demuestran que los cálculos de frecuencias y amortiguamientos usando los modos clásicos serán aproximaciones de primer orden de los valores exactos.