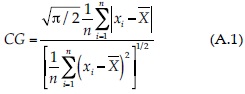
Apéndice 1: Referencias para 13 de las 16pruebas estadísticas aplicadas

1. Test del Cociente de Geary (CG)

Relaciona la desviación media absoluta del registro con su desviación estándar. Cuando el CG se aparta de la unidad, indica pérdida de normalidad. Su expresión es la siguiente (Machiwal & Jha, 2012):

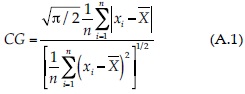
2. Test de Shapiro-Wilk (SW)

También conocido como Test W, emplea valores tabulados para calcular su estadístico. Su procedimiento y datos necesarios se pueden consultaren Shapiro y Wilk (1965), y en Ruiz-Maya (1977) para registros de hasta 50 datos, y en Shapiro (1998) para series de hasta 98 valores.

3. Prueba de Helmert (PH)

Esta es una prueba no paramétrica que se basa en secuencias y cambios respecto a la media, la cual se pueden consultar en Mather (1977) y Campos-Aranda (1998).

4. Prueba de las secuencias (PS)

Esta prueba no paramétrica emplea las secuencias que se forman respecto a la mediana; se pueden consultar en Thom (1971) y Campos-Aranda (1998).

5. Prueba de Von Neumann (PV)

Esta prueba paramétrica detecta pérdida de aleatoriedad por componentes determinísticas no especificadas; su procedimiento operativo se puede consultar en WMO (1971), Buishand (1982), y Machiwal y Jha (2012).

6. Test de Anderson de persistencia (TA)

Esta es una prueba paramétrica que se basa en el coeficiente de correlación serial de orden 1 (r₁), la cual se pueden consultar en WMO (1971), Linsley, Kohler y Paulhus (1988), y Campos-Aranda (1998).

7. Test de Sneyers de persistencia (TS)

Es una prueba no paramétrica, recomendada cuando el registro no es normal. Se puede consultar en WMO (1971), y Machiwal y Jha (2012).

11. Test de Bartlett de variabilidad (TB)

Esta prueba paramétrica, también llamada de homogeneidad de varianzas, busca inconsistencia debido a la dispersión. Su secuela se puede consultar en WMO (1971) y Ruiz-Maya (1977).

12. Test de Cramer de cambio en la media (TC)

Esta prueba no paramétrica compara la media de un subperiodo con la del registro; se puede consultar en WMO (1971) y Campos-Aranda (1998).

13-16. Tests de Buishand de cambio en la media (TB₁ a TB₄)

La gráfica de las desviaciones acumuladas con respecto de la media se denomina curva masa residual, permite reconocer fácilmente los cambios que han ocurrido en ésta y por ello Buishand (1982) presentó cuatro pruebas basadas en estadísticos (Q, R, U y A) tomados de tal curva. Aplicaciones de estas pruebas en México se pueden consultar en Gutiérrez-López, Arellano-Lara y Aparicio-Mijares (2007), y en Campos-Aranda (2008).

Apéndice 2: Descripción de los tres test de tendencia

Machiwal y Jha (2008) aplicaron 12 pruebas para detección de la tendencia, la mayoría paramétricas y encontraron que los tres test siguientes fueron los de mayor potencia o más confiables.

8. Test de Kendall (TK)

Esta prueba paramétrica también se conoce como de correlación de rangos (Machiwal & Jha, 2012). Es muy efectiva si la tendencia fundamental es de tipo lineal o se aproxima a ésta. Su procedimiento consiste en evaluar el número p en todos los pares de observaciones (x_i, x_j; con i = 1 a n - 1; j = i + 1 a n) en que x_j es mayor que x_i; después se calculan las estadísticas siguientes (Kottegoda, 1980):

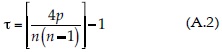
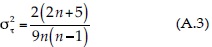
Si el cociente τ/σ_τ es menor que ±1.960, el registro no presenta tendencia en una prueba de dos colas con un nivel de significancia α de 5%.

9. Test de Spearman (TS₁)

En esta prueba no paramétrica, que se conoce como correlación del orden de rangos (Machiwal & Jha, 2012), primero se ordenan los datos de menor a mayor y se sustituye cada elemento del registro por su rango (k_i); después, para cada dato de la serie original, se calculan las diferencias: d_i = k_i -i, con i = 1 a n y se evalúan las estadísticas siguientes (WMO, 1971; Adeloye & Montaseri, 2002):

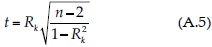
El valor de la ecuación anterior se compara con el intervalo que define ±t_c tomado de la distribución t de Student con n - 2 grados de libertad y nivel de significancia α, para una prueba de dos colas; si lo excede (t > t_c), existe tendencia.

10. Test de Mann-Kendall (TM)

Es una prueba no paramétrica que busca tendencia en la serie sin importar si es lineal o no lineal; pero el registro no debe mostrar persistencia. Su estadístico operativo Ss es la suma de los signos de las diferencias (z) de todas las parejas factibles de formar, por ello su expresión es (Manly, 2001):

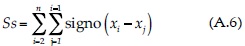
en la cual el signo (z) es -1 para z < 0, 0 para z = 0 y +1 para z > 0. Para una serie con valores aleatorios se espera que Ss = 0, cuya varianza es (Hirsch, Helsel, Cohn, & Gilroy, 1993; Machiwal & Jha, 2012):

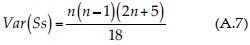
El estadístico de la prueba es:

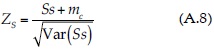
En la expresión anterior, m_c= 1 cuando Ss < 0 y m_c = -1 para Ss > 0. Si el valor absoluto de Z_S es mayor que el valor crítico de la distribución Normal estándar, la serie presenta tendencia creciente o decreciente con un nivel de significancia α. Para α = 5%, el valor crítico es 1.960. La varianza (ecuación (A.7)) se debe corregir cuando existen datos iguales o la muestra es censurada (Hirsch et al., 1993).

Hamed y Rao (1998) desarrollaron una corrección para la ecuación (A.7), que toma en cuenta la persistencia de la serie, la cual permite la aplicación del Test de Mann-Kendall a datos autocorrelacionados. Sonali y Nagesh-Kumar (2013) presentan dos enfoques de corrección de la prueba de Mann-Kendall basados en modificar su varianza (ecuación (A.7)). Kundzewicz y Robson (2004) exponen otros procedimientos de aplicación de la prueba de Mann-Kendall, los cuales utilizan el re-muestreo estadístico.

Apéndice 3: eliminación de la persistencia por pre-blanqueado del registro

Desde mediados de la década de 1990 se estableció que la correlación serial positiva de una muestra o registro incrementa la posibilidad de que el Test de Mann-Kendall (TM) detecte tendencia significativa. Para eliminar tal influencia se propuso el pre-blanqueado del registro, considerando que tal componente de correlación serial es un proceso autorregresivo de orden uno [AR(1)] y que por lo tanto debe ser retirado antes de aplicar el test TM (Burn & Hag-Elnur, 2002).

Posteriormente, Yue, Pilon, Phinney y Cavadias (2002) demostraron, mediante simulación aleatoria, que cuando un proceso AR(1) y una tendencia lineal existen en una serie, la remoción del proceso autorregresivo con el pre-blanqueado también elimina una parte de la tendencia. Lo anterior se observa considerando que un registro (X_t) está formado por una tendencia lineal (T_t = β·t) y un proceso AR(1), con r₁ como el coeficiente de correlación serial de orden uno y ε_t como el ruido blanco o componente aleatoria (A_t = r₁·A_t-1 + ε_t), es decir:

El registro preblanqueado será:

Sustituyendo en la expresión anterior la ecuación (A.9) y el proceso AR(1) se tiene:

Simplificando y agrupando se tiene:

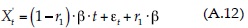
En la expresión anterior se observa que el proceso autorregresivo ha sido eliminado, pero ahora la pendiente de la serie pre-blanqueada es β' = (1 - r₁) · β; entonces, cuando se remueve un AR(1) positivo (r₁ > 0) se tiene que |β'| < |β|, indicando que el pre-blanqueado elimina parte de tendencia. Cuando AR(1) es negativo (r₁ < 0), ocurre lo contrario, |β'| > |β|, de manera que el pre-blanqueado incrementa la tendencia.

Debido a lo anterior, Yue et al. (2002), y Yue, Pilon y Phinney (2003) propusieron un pre-blanqueado libre de tendencia, que consiste en identificar la tendencia lineal (T_t) y retirarla de la serie (X_t), para obtener una muestra sin tendencia (Y_t), esto es:

Después se elimina el proceso AR(1), cuando el r₁ resultó estadísticamente significativo o diferente de cero, para obtener la serie de valores independientes (Y'_t), ésta es:

Finalmente, se suma la tendencia identificada para obtener una muestra mezclada (Y''_t),que incluye tendencia y otros componentes, como el ruido blanco, pero que no está influenciada por la correlación serial; a esta serie se le aplica el test de Mann-Kendall:

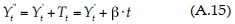
Apéndice 4: Recta de regresión para la tendencia lineal

Se considera que la variable dependiente (y) son las temperaturas anuales T_i en °C y los tiempos o años A_i son las abscisas (x), en este caso iguales al i-ésimo valor i. Para probar si la pendiente (m) de la recta de regresión ajustada por mínimos cuadrados de los residuos es estadísticamente diferente de cero, se usa una prueba basada en la t de Student definida por las ecuaciones siguientes (Ostle & Mensing, 1975):

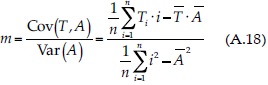
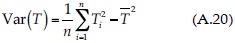
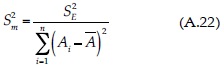
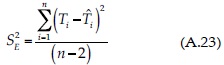
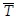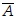y son las medias aritméticas; r_xy es el coeficiente de correlación, el cual varía de cero a ±1. La pendiente m tiene unidades de °C/año y la ordenada al origen b de °C. En la ecuación (A.23), 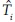es el valor estimado con la recta de regresión (ecuación (A.16)). 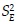y 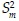son las varianzas de los errores y de la pendiente de la recta de regresión. Si el valor calculado t (ecuación (A.21)) es mayor que el crítico (t_c), obtenido para la distribución t de Student con n-2 grados de libertad y α = 5%, en una prueba de dos colas, la pendiente m es significativa, es decir, existe tendencia lineal. El problema de esta prueba es que no distingue entre persistencia y tendencia (Adeloye & Montaseri, 2002); además, la estimación de m es sensible a la no normalidad de los datos (Sen, 1968).

Apéndice 5: Pendiente de la tendencia (ms) según criterio de Pranab Kumar Sen

Sen (1968) propuso utilizar el criterio de análisis de la tendencia establecido en el test de Kendall para estimar su pendiente (ms), definiéndola como el valor mediano (MED) de las pendientes parciales, es decir:

X_j y X_i son los datos, en este caso temperaturas máximas de mayo, en los tiempos j e i, que son años; ms tiene unidades de °C/año. Siendo n el número de datos, entonces habrá n(n-1)/2 pendientes parciales. El signo positivo de ms define tendencias ascendentes y el negativo descendentes (Sonali & Nagesh-Kumar, 2013). Machiwal y Jha (2012) indican que la estimación ms es resistente o robusta a la presencia de valores dispersos (outliers).