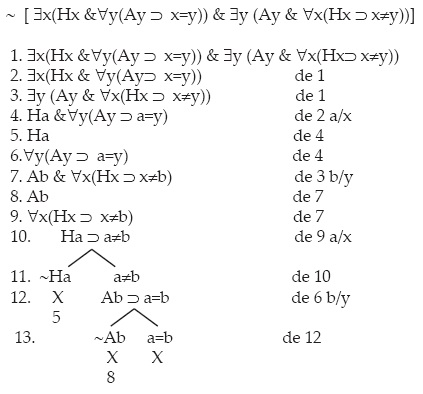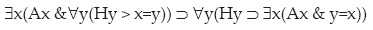
Apéndice
Mostramos:
1. Cómo es posible la subalternación inusual, pues va de una particular (conversa) a una universal (normal). Tomemos por caso
R*⊃A
o sea
[P](S) ⊃ (S)[P]
y en M: "si algún animal es todo hombre entonces todo hombre es algún animal".
En simbolismo actual tenemos:
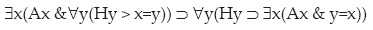
Donde el antecedente es particular y el consecuente es universal. Pero la inferencia es válida, pues realmente el cuantificador particular afecta al predicado A y el universal al sujeto H, tanto en el antecedente como en el consecuente. La negación de la fórmula produce un árbol cerrado, y presupone la simetría de la identidad, incluso en la forma negativa: si a no es b, b no es a, paso 15 abajo. Es éste:
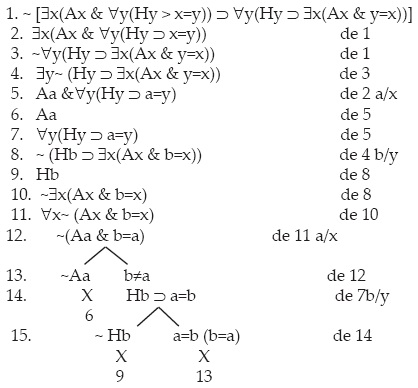
2. Cómo es posible que dos oraciones universales puedan ser subalternas, es decir, estar "abajo", en la posición de las subcontrarias. Tomemos
A v N*
O sea, las expresamos como subcontrarias, con una disyunción que expresa que pueden ser ambas verdaderas:
(S)[P] v (P)/[S]
en M: "Todo hombre es algún animal v todo animal no es algún hombre"
en simbolismo actual:
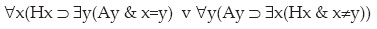
Cuya negación produce un árbol cerrado. Es este:
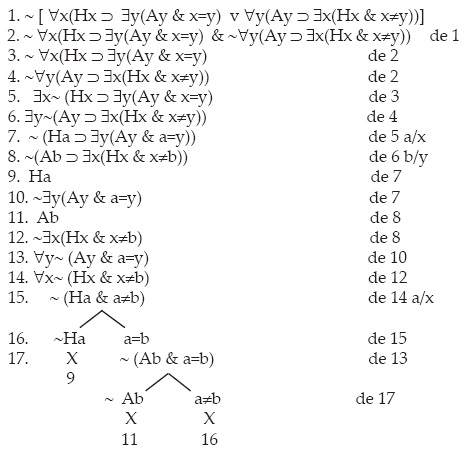
Finalmente mostramos que dos oraciones particulares pueden ser contrarias, es decir, no pueden ser ambas verdaderas. El teorema:
~ (R & O*)
Es decir: R y O* no pueden ser ambas verdaderas, conduce a contradicción y muestra un árbol cerrado.