1.Introduction
Materials, in general, have different mechanical properties, and consequently, body waves propagate differently inside of them. In the scientific community, there has always been an enormous interest in studying the propagation of body waves since they offer to determine in a non-invasive or destructive way, the mechanical properties of the medium through which they travel 1-5. Its study has allowed obtaining information on the structure and composition of our planet’s various layers 6. But they have also been of great help in seismic prospecting to locate oil deposits on land, shallow and deep waters 7.
Among the mechanical waves, the most technologically attractive are those known as interfacial waves, which emerge at the interface of two media due to the coupling of both shear and compression waves 8. The characteristics of this type of waves, which in turn make them easy to detect, are: a) they rapidly decay in-depth, b) they propagate parallel to the interface between two media, c) they have the largest amplitude, and d) they decay more slowly than body waves. There are three types of interfacial waves 9: a) the Stoneley wave that emerges at the interface of two solids, b) the Scholte wave that appears at a solid-fluid interface, and c) the Rayleigh wave or (surface wave) that arises in the free surface of a solid exposed to a vacuum. Although interface waves are commonly used to detect defects in the surface of materials 10,11, they can also be used to develop biosensors, temperature sensors, pressure sensors, and humidity sensors, among others 12,13. Due to the feasibility of the physical conditions under which Scholte waves can be excited and measured, so its characterization is very attractive for the development of technological devices with practical applications 14,15.
Theoretically, the zeros of Scholte’s secular equation determine the speed with which a wave moves at the solid/fluid interface 16. Before discussing the complexity of solving this equation, let us consider a particular case: the Rayleigh’s secular equation. This last equation was formulated for the first time by Lord Rayleigh 17, and it arises from posing the problem of the propagation of a wave (with speed C) along the free surface of an elastic and isotropic solid and is described as
Here A(C) and B(C) are in terms of α and β (the compressional and shear velocities, respectively) as
To find a distinct solution from the trivial one (C = 0) in Eq. (1), Lord Rayleigh
proposed to find solutions to
Note that the roots of Eq. (3) do not correspond to the problem of the Rayleigh wave propagation, but the equality
leads to the same polynomial as the one obtained by Rayleigh. Thus, it is evident
that this procedure introduces spurious roots that come from f(C).
Lord Rayleigh (based on physical arguments) showed for some particular cases, that
Eq. (1) has only one physically acceptable root, which should be real and with speed
As discussed above, the rationalization method restates the solution to Eq. (1) in terms of a third-order polynomial, the roots of which allow a piecewise solution to be constructed 20-24. The availability of analytical expressions for the respective complex roots may incorrectly suggest additional solutions 25 to Eq. (1). Nevertheless, due to the simplicity of the method, it has been used to investigate analytically the solutions of both Scholte and Stoneley secular Eqs.(26). However, because these equations have a larger number of square roots terms, the polynomial order increases, and consequently, the number of spurious roots introduced also increases. For these cases, even the numerical evaluation of the roots is not an easy task, and in the case of viscoelastic media, it is practically unthinkable. Nkemzi 27 and Romeo (19), in terms of a method based on Cauchy integrals, considered Eq. (1) for both the elastic and viscoelastic cases, respectively, and demonstrated the existence of only one physical solution. Later Antúnez-García would consider the same method to solve the Scholte equation for a specific range of fluid velocities, which would be extended by Vinh (29), both showing that it also has only one physical solution.
As previously shown, the Scholte secular equation’s parametrization in terms of the slowness drives directly to a unique physical solution of this expression 28 without any additional assumptions; then, we propose extending those results in the full range of possible fluid velocities. Unlike the work presented by Vinh 29, the current one makes a more detailed analysis of the solution’s behavior for the different speed ranges with which a wave can propagate in a fluid. So the relevance of the present work falls in obtaining a simple analytical expression to describe the slowness of the Scholte wave for all the range of possible elastic and isotropic media. We also show that the Rayleigh’s wave is a singular solution (at the free surface limit) that rises specifically at the connection point of two fluid speed ranges.
The article is organized as follows: Sec. 2 is devoted to give a brief introduction of the Scholte’s secular equation and the requirements for the existence of that solution. In Sec. 3, the quotient of discontinuities associated to the Scholte’s secular equation are analyzed, and the continuous continuation of them for different speed ranges was established. In Sec. 4 the expression for the unique physical root of the Scholte’s secular equation is obtained and particularly, it is used to recover the Rayleigh wave solution. Additionally, numerical calculations were included to test the solution of the Scholte’s equation. Finally, the conclusions are presented.
2.Scholte’s secular equation
In general the existence of a wave propagating through the interface of two homogeneous and isotropic semi-infinite media (exponentially decaying) was predicted by Stoneley . A particular case of a Stoneley wave arises when one of those semi-infinite media becomes fluid, which is known as a Scholte wave. The speed propagation of this wave (C) is a zero of the Scholte secular equation 26,31-33
under the following physical restrictions
which ensures solutions with an exponentially decaying behavior. Here α and β are the
compressional and shear velocities of elastic waves in a solid, CF is the
speed of a sound wave in a fluid, p and ρF are the densities of a solid
and fluid medium, respectively. Note that the terms inside of the square brackets in
Eq. (5) correspond to the Rayleigh characteristic Eq. (1). By convenience we rewrite
Eqs. (5) and (6) in therms of the dimensionless variable
subject to the restrictions
For any elastic and isotropic medium α, β, and CF are real and positive quantities. In particular, the ratio of speeds can be described in terms of Poisson’s (v) ratio as
Thus, there are three cases for the study of the characteristic Scholte equation (7):
(a)
3.Discontinuities of Scholte’s secular equation
In general the branch points of F(z) are localized along the real axes
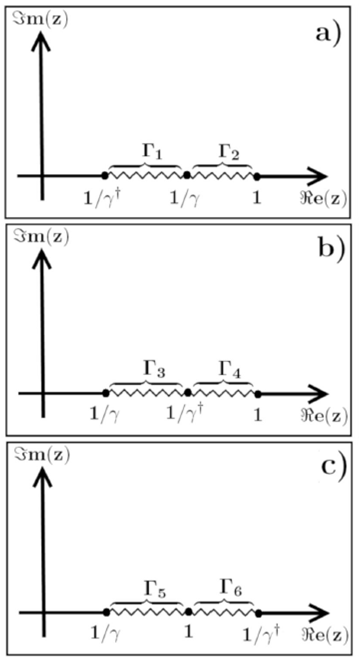
Figure 1 Branch cuts for the function F(z) for cases in which: a) CF > α > β, b) α > CF > β and c) α > β ¸ CF .
which describes the discontinuities presented by the Rayleigh secular equation 28.
3.1.Case (a):
For this case the arcs over which the discontinuities spans (see Fig. 1a)) are
The respective discontinuity quotient along each arc is described as
with the auxiliary functions
For the range of velocities under consideration, note that
guarantees the continuous continuation of these functions. The limit in which the
fluid vanishes (
Where
is the auxiliary function for the free surface limit 28. Otherwise, the corresponding auxiliary functions are described by Eq. (12).
Moreover, it is prohibitive that 
Thus, while a fluid under which the solid-fluid interface may be defined, the contribution to the fluid discontinuities will be distinct to the free-surface limit.
3.2.Case (b):
For a fluid under this range of velocities, the discontinuities (see Fig. 1b)) are described by
with the auxiliary functions
which are defined along the arcs
Here the continuous continuation and unicity of solutions is granted by
while for the limit with
as in the previous case. Particularly for this case, note that the Rayleigh
branch cut
Thus the connection of discontinuities on both cases (a) and (b) is granted trough the free-surface limit.
Contrarily to the unscreened Rayleigh branch cut limit, the full-screening of
and
then, the extreme values of 𝐺 3 (𝑡), particularly corresponds to well-defined values
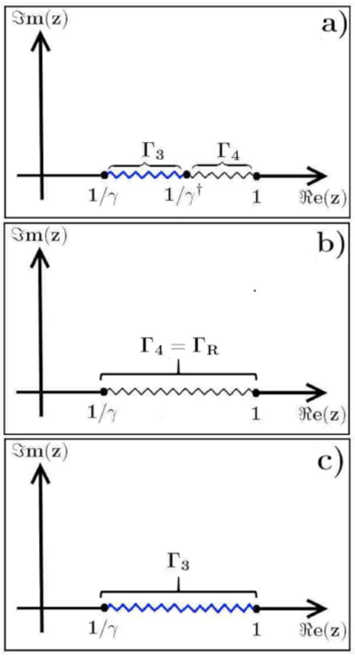
Figure 2 Branch cuts for the function F(z) in the case that α > C F > β for: a) the general case, b) p F → 0 and c) 1= y† → 1. The branch cut colored in blue represents the fluid discontinuities’ contribution to the three different cases. The cases in which Γ R is totally unscreened and totally screened correspond to Figures b) and c) respectively.
3.3.Case (c):
Within this range of velocities, the discontinuities (see Fig. 1c)) are described by
along the branch cuts
with the auxiliary functions
It should be noted that the lowest value which 
Which establishes the continuous continuation between G3 and
G5. On the other hand, for the limit in which
Here
4.The Scholte solution
Since we have guaranteed the continuous continuation of the Scholte discontinuities for the entire range of fluid velocities, we are in a position to determine the polynomial containing the zeros of Eq. (7). According to the construction 5 for the canonical solution of the Riemann problem, the polynomial with only zeros of the Scholte characteristic Eq. (7) is
which was obtained through the Bourniston method . This method involves the expansion of Eq. (A.3) in terms of Laurent series. It should be noted that unlike previous works 19,27,29, the parametrization in terms of slowness conduces directly to a simple polynomial (26), and additional considerations are not necessary to solve it. In fact, directly from this polynomial is possible to have one and only one physical solution for the Scholte slowness, that is
Here δ is a correction parameter introduced to enhance the numerical accuracy of the
Scholte root, which is a consequence of the truncation process during the Laurent
series expansion (Eq. (7)). The
4.1.The free surface limit
Contributions associated exclusively with the
or explicitly to
which, according to 28, describes the exact slowness of the Rayleigh’s wave propagation. Note that the δ term is not included in this expression.
4.2.Numerical Results
To numerically test the expression in Eq. (27) for different solid-fluid interfaces, we have used the parameters in Table I to illustrate the numerical derivation of the root in each of the three different fluid speed ranges. Wolfram Mathematica software was used to implement this expression numerically. The root calculated from Eq. (27) was compared with that obtained from Eq. (5) utilizing a root finder routine (provided by the software). It should be noted that not in all cases, the root finder routine was able to obtain the correct value, even when the provided value was close to the zero.
Table I Input parameters for the different solid (S i ) and fluid (F i ) materials under consideration.
| Material | Label | Density [Kg/m3] | Compressional Speed [m/s] | Shear Speed [m/s] |
| 7-A teflon a | S1 | 2157.7 | 1307 | 503 |
| Lucite b | S2 | 1180 | 2680 | 1100 |
| Silver b | S3 | 10400 | 3650 | 1610 |
| Berylium b | S4 | 1870 | 12890 | 8880 |
| Ice-1 c | S5 | 344 | 440 | 304 |
| Ice-2 d | S6 | 442 | 1472 | 755 |
| Ice-3 e | S7 | 637 | 2709 | 1489 |
| Water (Distilled) b | F1 | 998 | 1496 | - |
| Air (dry) b | F2 | 1.293 | 331.45 | - |
| Sea Water f | F3 | 1028.15 | 1442.45 | - |
aReference 35. bReference 36. cValues taken at sea level 37. dValues taken at 5 mts depth 37. eValues taken at 20 mts depth 37. f Density computed at sea level, 0oC, 30 PSU salinity and 1 Atm.38. Compressional speed taken from Ref.39.
Table II (for distinct solid-fluid
interfaces) shows the corrected (
Table II Values for the associated Poisson’s ratio º for each solid-fluid interface (Si ¡Fj ), corrected and uncorrected roots, the correction parameter ± and the precision of the corrected root ¢ associated to this parameter.
| Interface | ν | z Sc (Uncorrected) | z Sc (Corrected) | δ | ∆ |
| S1 − F1 | 0.4103 | 1.33931 | 1.28279 | 0.54107 | 4.19 × 10−6 |
| S2 − F2 | 0.3987 | 1.63185 | 1.54761 | 0.40354 | 2.78 × 10−6 |
| S3 − F1 | 0.3792 | 1.34904 | 1.25176 | 3.702 | 6.6 × 10−6 |
| S3 − F2 | 0.3792 | 23.69205 | 23.59477 | 2857.6 | 2.2 × 10−7 |
| S4 − F1 | 0.04836 | 35.47909 | 35.24175 | 0.6781 | 6.3 × 10−6 |
| S4 − F2 | 0.04836 | 718.29634 | 717.77757 | 1144.4 | 1.2 × 10−5 |
| S5 − F3 | 0.0433 | 3.8311 | 3.8089 | 0.0112 | 3.18 × 10−6 |
| S6 − F3 | 0.3215 | 2.6407 | 2.5092 | 0.1624 | 5.27 × 10−6 |
| S7 − F3 | 0.2835 | 1.8804 | 1.7293 | 0.5555 | 2.36 × 10−6 |
The results are summarized in Table II. A
direct comparison of these values shows that the uncorrected root presents a
relative error
5.Conclusions
In terms of Cauchy integrals, we have obtained a robust analytic formula to predict the existence of a unique physical solution for the Scholte slowness in all range of possible elastic and isotropic media.The appropriated analysis of the discontinuities associated to the Scholte secular equation allows us to identify the free-surface limit as a pole contribution.
Unlike previous results 29, due to the secular Scholte equation’s fractional-order, our results show that the truncation process involved in obtaining the rational polynomial does not allow getting an exact solution. However, our numerical results show that this solution presents a reasonable approximation to the exact value. Additionally, since slowness is the inverse of speed, the results show that a Scholte wave’s propagation speed is less than or equal to that of a Rayleigh wave.











 nueva página del texto (beta)
nueva página del texto (beta)



