1. Introduction

I understand metaphysics as a rational enterprise whose main goal is to articulate the most coherent worldview that emerges from our current scientific knowledge. It is the goal of metaphysics to explain concepts such as those of natural law, cause, space, time, chance, emergence, property, and the like on the basis on what actual research in all areas of science informs us. Whether the metaphysician succeeds or fails in his or her efforts depends in good measure on the quality and correctness of the scientific views adopted. Hardly anything interesting can be said about the real world if we conceive it as formed just by the objects given by ordinary sense or ancient and outdated theories of matter. The world revealed by contemporary science is much more complex, manifold, and stranger than what was imagined by the ancient Greeks or the mechanistic philosophers of the 17th and 18th centuries. Although many philosophical systems of the past still can be seen as grandiose and inspiring intellectual achievements, their foundations in the science of their own time have been shaken. A reconstruction is needed. Metaphysics should evolve along with science, because it is through science that it makes contact with the world it aims to interpret. Many recent discoveries in special sciences are so counterintuitive that attempts at building metaphysical systems based upon common sense and a priori judgements regularly yield ridiculous and utterly useless results.

In a recent book a couple of well-known philosophers complained: "A key general grievance we raise against traditional metaphysician is that in continuously constructing simplistic caricatures of science, they render it substantially less interesting than it really is" (^{Ladyman and Ross 2009, p. 22}).

They then go on to say: "Mainstream contemporary analytic metaphysics has, like the nineteenth-century metaphysics against which Russell revolted, become almost entirely a priori. Metaphysics informed by real physics is much less common" (^{Ladyman and Ross 2009, p. 24}).

I think that these criticisms are to the point. Metaphysics cannot, and certainly should not, try to offer a final, ultimate worldview. It should evolve with science and in accordance with what the special sciences have to tell us about the world. And from there it should move on to elaborate always provisional general truths about whatever is thought to exist. This requirement of keeping up with the science of the day goes even beyond metaphysics and encompasses all philosophy. As requested long ago by Hans ^{Reichenbach (1951)}, true philosophy should be scientific philosophy, i.e. philosophy based on the best current science.¹

Of all special sciences, it is undoubtedly modern physics which has had the strongest impact on reshaping our metaphysical views. Both Quantum Mechanics and General Relativity have had profound effects on metaphysics, calling to revise the very foundations of what we understand by matter, physical laws, space, and time. Current scientific discoveries in astrophysics and cosmology have also extraordinary significance for the philosopher, although their implications have been difficult to perceive because of the technicalities involved. The recognition of the existence of black hole solutions to Einstein's field equations in the early 1960s and the recent confirmation of their existence by the detection of gravitational waves and direct imaging of the event horizon of the black hole in the nearby galaxy M87 are landmarks of lasting philosophical consequence.

The philosophical problems related to black holes remain mostly unexplored, despite their richness and vast scope. An early philosophical discussion of black holes was given by ^{Weingard (1979)} and some additional issues were discussed by ^{Earman (1995)}, ^{Romero (2013b}, ^2014a, ^2014b, ^2016b), and ^{Romero and Pérez (2014)}. Papers with various philosophical implications of black holes have been published recently by ^{Curiel (2019)}, who deals with the many definitions of black holes, ^{Maudlin (2017)} and ^{Manchak and Weatherall (2018)}, who discuss the firewall paradoxes, ^{Lesourd (2019)}, who investigates the causal structure of evaporating black holes, and by John ^{Dougherty and Craig Callender (2016)}, who discuss philosophical aspects of black hole thermodynamics. Also, some philosophical issues are to be found in the specialized scientific literature, which remains almost inaccessible to most philosophers. The interested reader can check the entry by ^{Curiel (2021)} in the Stanford Encyclopedia of Philosophy for a review of some relevant literature on the topic.

In this paper I offer a survey and some fresh discussions of a few interesting philosophical issues motivated by black hole physics. I hope that this selection, which in no way is complete, will prompt further philosophical research on the ontological and epistemological problems posed by the existence of black holes. It is unavoidable for an article such as this one to resort to some technicalities. For this reason the first three sections review some basic concepts of black hole physics. Those readers feeling that some extra background is necessary for a better understanding of what follows might find useful the books by ^{Raine and Thomas (2010)}, ^{Frolov and Novikov (1997)}, ^{Poisson (2004)}, ^{Frolov and Zelnikov (2011)} or my own book with G. Vila (2014). Clear introductions to General Relativity are, for instance, ^{Hobson et al. 2006}, ^{Joshi 1993}, and ^{Wald 1984}. Sections 6- 14 of the article cover many different problems related to black holes including determinism, singularities, information, predictability, supertasks, the direction of time, the controversies of relationism versus substantivalism and presentism versus eternalism, as well as the ontological status of black holes.

I will start introducing some definitions and useful concepts.

2. Definitions

Black holes are gravitationally collapsed objects and, therefore, they are infinitely redshifted.² This means that they are causally disconnected from the rest of the universe in the following sense: events occurring inside the black hole can never affect in any way events occurring outside. A crucial issue, then, is to provide an adequate definition of the boundary between the interior and exterior regions of the black hole. In order to give such a definition, let us introduce first a physical system which contains all events. An event is an occurrence of any type. We call such a system spacetime and we represent it by a C^∞-differentiable, 4-dimensional (4D), real pseudo-Riemannian manifold.³ A real 4D manifold is a topological space with the property that each point has a neighborhood that is homeomorphic to subsets of ℜ⁴, the 4-dimensional space of real numbers. We adopt 4 dimensions because it seems enough to give 4 real numbers to localize an event. A metric field g_μv that determines the distance between two events and is locally Minkowskian is introduced on the manifold in accordance with Einstein's field equations (EFEs):

where R_μv is the Ricci tensor formed with second order derivatives of the metric, R is the Ricci scalar g^μvR_μv, k=8πG/c⁴ is a constant, and T_μv is a second rank tensor that represents the energy-momentum of all physical fields. The set {x^μ} is a mathematical coordinate system that is attached to a physical reference frame (an insightful discussion on coordinate systems and their relationship with reference frames is given by ^{Bunge 1967}). A given spacetime model is specified by a triplet: ST ≡ (M , g, T), where M is the manifold, g the metric field, and T the energy-momentum field. Since we will deal with vacuum or electro-vacuum solutions when discussing most types of black holes, for simplicity, I will denote a given space-time by (M, g).

Because many coordinate systems can be used to describe black holes, it is convenient to give a definition of a black hole that is independent of any specific choice of coordinates. But first, I will introduce some preliminary useful definitions.⁴

DEFINITION. A causal curve in a spacetime (M , g ) is a curve that is non spacelike, that is, piecewise either timelike or null (light-like).

We say that a spacetime (M , g ) is time-orientable if we can define over M a smooth non-vanishing timelike vector field.

DEFINITION. If (M , g ) is a time-orientable spacetime, then ∀p ∈ M, the causal future of p, denoted J⁺(p), is defined by:

J⁺(p)≡{q∈M |∃ a future-directed causal curve from p to q}.

Similarly,

DEFINITION. If (M, g ) is a time-orientable spacetime, then ∀p ∈ M, the causal past of p, denoted J^—(p), is defined by:

J^—(p)≡{q∈M |∃ a past-directed causal curve from p to q}.

The causal future (+) and past (-) of any set S ⸦ M are given by:

A set S is said to be achronal if no two points of S are timelike related. A Cauchy surface is an achronal surface such that every inextendible differentiable non spacelike curve in M crosses it once, and only once. A spacetime (M, g ) is globally hyperbolic iff it admits a spacelike hypersurface S ⸦ M which is a Cauchy surface for M.

Causal relations are invariant under conformal transformations of the metric. So, the spacetimes M,g and M,g~, where g~=Ω2g, with Ω a non-zero C^r function, have the same causal structure.

Let us now consider a spacetime where all null geodesics that start in a region J^— end at J⁺ . Then, such a spacetime, (M , g ), is said to contain a black hole if M is not contained in J^—(J⁺). In other words, there is a region from where no null geodesic can reach the asymptotic flat⁵ future spacetime, or, equivalently, there is a region of M that is causally disconnected from the global future. The black hole region, BH, of such spacetime is BH = [M - J^—(J⁺ )], and the boundary of BH in M, H = J^— (J⁺) ∩ M, is the event horizon.⁶

Notice that a black hole is conceived as a spacetime region, i.e. what characterizes the black hole is the metric and, consequently, the associated curvature. What is peculiar of this spacetime region is that it is causally disconnected from the rest of the spacetime: no events in this region can make any influence on events outside the region. Hence the name of the boundary, event horizon: events inside the black hole are separated from events in the global external future of spacetime. The events in the black hole, nonetheless, as all events, are causally determined by past events. A black hole does not represent a breakdown of classical causality.

A useful representation of a black hole is given by a Carter-Penrose diagram. This is a two-dimensional diagram that captures the causal relations between different points in spacetime. It is an extension of a Minkowski diagram.⁷ The main difference with a Minkowski diagram is that, locally, the metric on a Carter-Penrose diagram is conformally equivalent⁸ to the actual metric in spacetime. The conformal factor is chosen such that the entire infinite spacetime is transformed into a Carter-Penrose diagram of finite size. For spherically symmetric spacetimes, every point in the diagram corresponds to a 2-sphere. In Figure 1, I show a Carter-Penrose diagram of a spherically symmetric vacuum (Schwarzschild) spacetime. The black hole is the region between the horizon and the jagged line at r = 0, which strictly speaking does not belong to spacetime because the model is singular there. It is clear that the term "black hole" denotes a region of spacetime, characterized by a particular metric structure.

Figure 1 Carter-Penrose diagram of a Schwarzschild black hole. The blue continuous line corresponds to the trajectory of the physical object falling into the black hole. 

The definition of horizon provided above corresponds to stationary black holes. The correct characterization of the horizon requires a knowledge of the entire spacetime. In dynamical situations, local or quasi-local definitions of the horizon are necessary. This a rather complex issue, but the distinction might be important in a number of situations of philosophical significance. I refer the reader to the well-known works by ^{Booth (2005)} and ^{Faraoni (2015)} for details. In what follows I offer just some elementary notions of trapped horizons, that in most dynamical situations play the role of the local horizons separating a black hole from the rest of the spacetime.

Intuitively, a horizon is a boundary between events observable and events unobservable. In case of a dynamical situation, to characterize such a boundary becomes tricky, and the best approach is to analyze what happens locally with bundles of light rays. This local concept is best captured by trapping surfaces from where light rays cannot reach infinity. More specifically, the trapping horizons of a spacetime are defined as the surfaces where null geodesics change their focusing properties. Mathematically, this kind of horizon is determined by the condition

where θ_in stands for the expansion of ingoing radial null geodesics while θ_out denotes the expansion of outgoing radial null geodesics, respectively. Regions where θ_inθ_out<0 are called regular. In the opposite case, θ_inθ_out>0, the region is called anti-trapped if θ_in > 0 and θ_out > 0, and trapped if θ_in < 0 and θ_out < 0. The trapped surfaces delimit (enclose) the dynamical black hole.⁹

3. Metrics and Properties

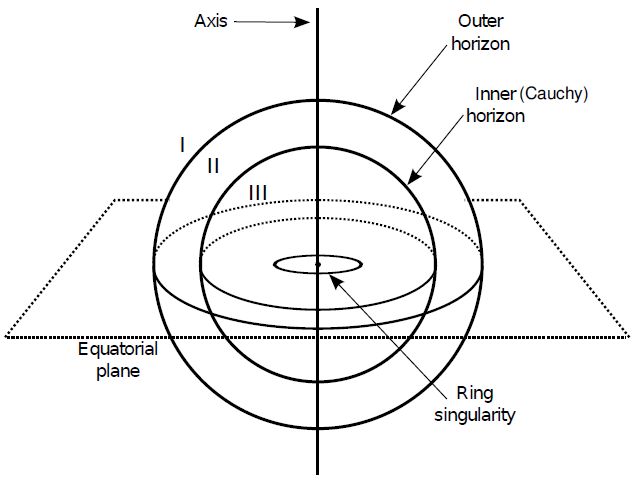
Exact solutions of Einstein's field equations representing stationary black holes exist for vacuum and electro-vacuum spacetimes. The spherically symmetric solutions are the Schwarzschild and Reissner- Nordström solutions, whereas the axially symmetric solutions are the Kerr and Kerr-Newman solutions. The Kerr-Newman metric of a charged spinning black hole is the most general black hole solution. It was found by Ezra "Ted" Newman and co-workers in 1965 (^{Newman et al. 1965}), and in the appropriate limits allows us to recover the other solutions.

The full expression of the interval¹⁰ in the Kerr-Newman space-time reads:

where M is the black hole mass, a = J/M is the specific angular momentum, q is related to the electric charge Q by

and the outer horizon is located at

There is an inner event horizon located at:

An essential singularity¹¹ occurs when g_tt → ∞; this happens if Σ = 0. This condition implies:

Such a condition is fulfilled only by r = 0 and θ=π2. This translates in Cartesian coordinates to:¹²

The singularity is a ring of radius ac^-1 on the equatorial plane. If a = 0, then a Schwarzschild's point-like singularity is recovered. If a ≠ 0 the singularity is not necessarily in the future of all events at r<rhinn: this means that the singularity can be avoided by some geodesics.

The Kerr-Newman solution is a non-vacuum solution. It shares with the Kerr and Reissner- Nordström solutions the existence of two horizons, and, like the Kerr solution, it presents an ergosphere (a region where spacetime is dragged around the black hole). At a latitude θ, the radial coordinate for the ergosphere is:

As is the case with the Kerr metric for an uncharged rotating mass, the Kerr-Newman interior solution exists mathematically but is probably not representative of the actual metric of a physically realistic rotating black hole because of stability problems.¹³ The surface area of the horizon is:

The Kerr-Newman metric represents the simplest stationary, axisymmetric, asymptotically flat solution of Einstein's equations in the presence of an electromagnetic field in four dimensions. Any Kerr-Newman source has its rotation axis aligned with its magnetic axis. Thus, a Kerr-Newman black hole is different from commonly observed astronomical bodies, for which there might be a substantial angle between the rotation axis and the magnetic moment (as observed in pulsars). In Figure 2, I present a sketch of the structure of a theoretical Kerr-Newman black hole.

Figure 2 Sketch showing the formal structure of a Kerr-Newman black hole. 

4. Thermodynamics

The area of a Schwarzschild black hole is

In the case of a Kerr-Newman black hole,

Notice that expression (19) reduces to (18) for a = Q = 0.

When a black hole absorbs a mass δM, its mass increases to M + δM, and hence, the area increases as well. Since the horizon can be crossed in just one direction, the area of a black hole can only increase. This suggests an analogy with entropy (^{Bekenstein 1973}). A variation in the entropy of the black hole will be related to the heat (δQ) absorbed through the following equation:

Particles trapped in the black hole will have a wavelength:

where k is the Boltzmann constant, and the proportionality requires a constant smaller than 1. Then,

where ξ is the mentioned numerical constant. Hence, we can associate a temperature with the black hole:

The corresponding entropy is:

A quantum mechanical calculation of the horizon temperature in the Schwarzschild case leads to ξ = (4π)^-1. So,

Then, we can write the entropy of the black hole as:

The formation of a black hole implies a huge increase of entropy: a star has an entropy ~ 20 orders of magnitude lower than the corresponding black hole. This tremendous increase of entropy is related to the loss of all the structure of the original system (a collapsing star or a cloud of gas) once the black hole is formed.¹⁴

The analogy between area and entropy allows us to state a set of laws for black hole thermodynamics (^{Bardeen et al. 1973}):

The association of a temperature with black holes has an immediate and strange consequence. All physical objects with non-zero temperature radiate. If the system is in thermal equilibrium its radiation has a Planckian spectrum. If black holes radiate, then their area and mass should decrease, so they should evaporate. How is such a thing possible?

5. Quantum Fields around Black Holes

In the current physical view, the world is a collection of quantum fields existing in spacetime. The vacuum state |0) of these fields can be excited to form a Fock basis of the quantized field:

Successive applications of the operator ak† yield:

This operator represents the property of the field of being excited. Each discrete excitation corresponds to what in classical physics is called "a particle".

In Minkowski space, a preferred basis can be constructed using the specific symmetries of this space (the Poincaré group). Then, if Nk=ak†ak is the particle number operator, we get

This means that the expectation value for all quantum modes of the vacuum is zero: if there are no particles associated with the vacuum state in one reference system, then the same is valid in all related inertial systems. In curved spacetime this is not valid any longer: general spaces do not share the Minkowski symmetries, and hence the number of particles is not a relativistic invariant. In particular, the presence of a black hole horizon induces a polarization of the vacuum in such a way that a detector at infinity will measure a net flux of thermal particles:

where ĸ = 8πG/c⁴, as before. The radiation has a Planckian distribution with a temperature T_BH = ĸ/2πk, in agreement with Eq. (22).¹⁵ Therefore, quantum field theory reveals the mechanism hidden behind the phenomenological considerations of the previous section. It is not the black hole that emits thermal radiation, but the quantum fields in the presence of the event horizon.

I now turn to more philosophical issues, starting with the problem of predictability in spacetimes with a black hole.

6. Determinism and Predictability in Black Hole Spacetimes

Determinism is a metaphysical doctrine about the nature of the world. It makes a basic ontological assumption: that all events are given. This supposition can be traced to Parmenides and his argument for necessary existence (^{Romero 2012}). It is important to emphasize that determinism does not require causality and does not imply predictability. Predictability is a property of our theories about the world, not a property of the world itself.

The confusion between determinism and predictability can be traced to Pierre-Simon Laplace and his Philosophical Essay on Probabilities:

We may regard the present state of the Universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the Universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes. (^{Laplace 1902 [1814]})

According to Laplace, every state of the Universe is determined by a set of initial conditions and the laws of physics. Since the laws are represented usually by differential equations and there are theorems for the existence and uniqueness of solutions, determinism implies predictability. Theorems apply, however, only to mathematical objects, not to reality. The world is not mathematical, just some of our representations of some aspects of the world take mathematical form. The existence of solutions to some equations that represent physical laws does not imply physical existence. Physical existence is independent of our conceptions. Moreover, even in Newtonian spacetimes there are Cauchy horizons that imply a breakdown of predictability (^{Earman 1986}).

In order to characterize Cauchy horizons let us first call to mind the definition of a Cauchy surface. Let (M , g ) be a smooth spacetime. We say that a set S ⸦ M is achronal if no two points are timelike related. Then, a Cauchy surface Σ is an achronal hypersurface of M for which the initial value problem for the dynamical equations of the matter fields defined on M are well-defined, i.e. for any smooth data in L₂(Σ) with finite energy, for the fields Φ, there is a unique solution Φ on M. Now, a Cauchy horizon is a hypersurface which fails to be a Cauchy surface in the sense that, even in the case of a complete specification of initial data L₂(Σ), the solutions of the dynamical equations cannot predict all events in the causal future of Σ. A manifold (without boundary) is globally hyperbolic if it admits a foliation by Cauchy surfaces. The presence of Cauchy horizons, then, destroys global hyperbolicity.

In classical physics, spacetime is not globally hyperbolic because of the absence of an upper bound on the velocities of moving bodies and fields in Newtonian spacetime.¹⁶ For instance, consider the trajectory of an object that is accelerated in such a way that its velocity becomes in effect infinite in a finite time. This object will be disconnected from events occurring at later times.

General Relativity assumes the existence of all events represented by a manifold. Hence, it is a deterministic theory from an ontological point of view. The Cauchy problem, however, cannot always be solved in General Relativity. Cauchy horizons naturally appear in many solutions of EFEs, and in particular, in those of rotating black holes. The inner horizons of both Kerr and Kerr-Newman black holes are Cauchy horizons: it is impossible to predict the evolution of any physical system in the interior region from the specification of the initial conditions over the horizon and EFEs.

Although the manifold is fixed, we cannot always describe it using the theory, even in the hypothetical case of a perfect knowledge. General Relativity is an example of a physical theory that can be ontologically deterministic but nonetheless epistemically underdetermined.

In addition to the presence of Cauchy horizons, the standard black hole spacetime models are singular. This means that all standard black hole solutions present essential divergences where the curvature and other scalars are unbounded. These divergences occur within the horizons. They imply that the models are incomplete in the sense that there are events that cannot be represented within the theory.¹⁷ Although the singularities can be avoided through modifications in the models, introducing peculiar fields fine-tuned to cancel the divergences, it is not clear whether such fields correspond to something that might actually exist.¹⁸

In any case, the existence of singular spacetime models does not imply a breakdown of the ontological determinacy of the theory. Singularities certainly imply a failure in the predictability of the models, but they are not elements of spacetime itself. I will say more on this below.

The fact that there exist irreversible processes in the universe implies that spacetime is globally asymmetric. The laws that constrain the space-state of physical fields, however, are invariant under time reversal.¹⁹ This is a classical problem of physics since Boltzmann and Loschmidt discussed it in the 19th century. Black holes might play a crucial role to link the global structure of spacetime to the local irreversibility expressed by the Second Law of Thermodynamics. I turn now to this problem.

7. Second Law and the Asymmetry of Time

The Second Law of Thermodynamics states that the entropy of a closed system never decreases. If entropy is denoted by S and the proper time of the system by τ, this law reads:

In the 1870s Ludwig Boltzmann argued that the effect of randomly moving gas molecules is to ensure that the entropy of a gas would increase, until reaching its maximum possible value. This is his famous H-theorem. Boltzmann was able to show that macroscopic distributions of great inhomogeneity (i.e. of high order or low entropy) are formed from relatively few microstate arrangements of molecules, and were, consequently, relatively improbable. Since physical systems do not tend to go into states that are less probable than the states they are in, it follows that any system would evolve toward the macrostate that is consistent with the larger number of microstates. The number of microstates and the entropy of the system are related by the fundamental formula:

where k = 10^-23 JK^-1 is Boltzmann's constant and W is the volume of the phase-space that corresponds to the macrostate of entropy S.

More than twenty years after the publication of Boltzmann's fundamental papers on kinetic theory, it was pointed out by ^{Burbury (1894}, ¹⁸⁹⁵⁾ that the source of asymmetry in the H-theorem is the implicit assumption that the motions of the gas molecules are independent before they collide and not afterwards. This means that the entropy increases as a consequence of the initial conditions imposed upon the state of the system. Boltzmann's response was:

There must then be in the universe, which is in thermal equilibrium as a whole and therefore dead, here and there, relatively small regions of the size of our world, which during the relatively short time of eons deviate significantly from thermal equilibrium. Among these worlds the state probability increases as often as it decreases. (1895)

As noted by ^{Price (2004)}: "The low-entropy condition of our region seems to be associated entirely with a low-energy condition in our past."

The probability of the large fluctuations required for the formation of the universe we see, on other hand, seems to be zero, as noted long ago by ^{Eddington (1931)}: "A universe containing mathematical physicists at any assigned date will be in the state of maximum disorganization which is not inconsistent with the existence of such creatures." Large fluctuations are rare (P ~ exp - ΔS); extremely large fluctuations, essentially impossible. For the whole universe, ΔS ~ 10¹⁰⁴ in units of k =1. This yields P = 0.

In 1876, a former teacher of Boltzmann and later colleague at the University of Vienna, J. Loschmidt, noted: "Obviously, in every arbitrary system the course of events must become retrograde when the velocities of all its elements are reversed" (^{Loschmidt 1876}).

In modern terminology, the equations that represent the laws of (Hamiltonian) mechanics are such that for every solution one can construct another solution by reversing all velocities and replacing t by - t. Since the Boltzmann's function H[f ] is invariant under velocity reversal, it follows that if H[f ] decreases for the first solution, it will increase for the second. Accordingly, the reversibility objection is that the H-theorem cannot be a general theorem for all mechanical evolutions of the system. More generally, the problem goes far beyond classical mechanics and encompasses our whole representation of the physical world. This is because the formal representations of the fundamental laws of physics are invariant under the operation of time reversal. Nonetheless, the evolution of all physical processes in the actual universe is irreversible.

If we accept, as mentioned, that the origin of the irreversibility is not in the laws but in the initial conditions of the laws, two additional problems emerge: 1) What were exactly these initial conditions?, and 2) How the initial conditions, of global nature, can enforce, at any particular time and place, the observed local irreversibility?

The first problem is, in turn, related to the following one, once the cosmological setting is taken into account: in the past, the universe was hotter and at some point matter and radiation were in thermal equilibrium as indicated by the cosmic microwave background (CMB) radiation;²⁰ how is this compatible with the fact that entropy has always been increasing according to the so-called Past Hypothesis?²¹

The standard answer to this question invokes the expansion of the universe: as the universe expanded, the maximum possible entropy increased with the size of the universe, but the actual entropy was left well behind the permitted maximum. The source of irreversibility in the Second Law of Thermodynamics is the trend of the entropy to reach the allowed maximum. According to this view, the universe actually began in a state of maximum entropy, but due to the expansion, it was still possible for the entropy to continue growing.

The main problem with this line of thought is that is not true that the universe was in a state of maximum disorder at some early time. In fact, although locally matter and radiation might have been in thermal equilibrium, this situation occurred in a regime where the global effects of gravity cannot be ignored (^{Penrose 1979}). Since gravity is attractive and the universe was extremely smooth (i.e structureless) in early times, as indicated, for instance, by the measurements of the anisotropies in the cosmic microwave background radiation (e.g. ^{Planck Collaboration 2020}), the gravitational field should have been quite far from equilibrium, with very low global entropy (^{Penrose 1979}). It seems, then, that the early universe was globally out of equilibrium, the total entropy being dominated by the entropy of the gravitational field. If we denote by C² a scalar formed by contractions of the Weyl tensor,²² the initial condition C² ~ 0 is required if entropy is still growing today.²³

The answer to the second question posed above, namely, "how the Second Law is locally enforced by the initial conditions, which are of global nature?", seems to require a coupling between gravitation (of global nature) and electrodynamics (of local action). Black holes might provide the key to understand this coupling.²⁴

The electromagnetic radiation field can be described in the terms of the 4-potential A^μ, which in the Lorentz gauge satisfies Maxwell equations:

with c =1 and j^v the 4-current. The solution A^v is a functional of the sources j^v. The retarded and advanced solutions are:

The two functionals of jμr→,t are related to one another by a time reversal transformation. The solution (32) is contributed by sources in the past of the spacetime point pr→,t where the field is determined, and the solution (33) by sources in the future of that point. The integrals in the second term on the right side are the surface integrals that give the contributions from i) sources outside of the volume V and ii) source-free radiation. If V is the causal past and future, the surface integrals do not contribute.

The linear combinations of electromagnetic solutions are also solutions, since the equations are linear and the Principle of Superposition holds. It is usual to consider only the retarded potential as physically meaningful in order to estimate the electromagnetic field at pr→,t:Fretμv=∂μAretv-∂vAretμ, However, there seems to be no compelling reason for such a choice. We can adopt, for instance (in what follows I use a simplified notation),

Here we set V_ret = J^-(p) and V_adv = J⁺(p).²⁵

If the spacetime is curved (R^μvδηR_μvδη ≠ 0), the null cones that determine the causal structure may not be symmetric around the point pr→,t. In particular, the presence of event horizons can make the contributions from both integrals very different because charges hidden by them can no longer affect events outside.

Hawking's black hole area theorem (^{Hawking 1971)} ensures that in a time-orientable spacetime such that for all null vectors k^μ holds R_μvk^μk^v≥ 0, the area of the event horizons of black holes either remains the same or increases with cosmic time. More precisely:

THEOREM. Let (M, g_μv ) be a time-orientable spacetime such that R_μvk^μk^v≥ 0 for all null k^μ. Let Σ₁and Σ₂be spacelike Cauchy surfaces for the globally hyperbolic region of the spacetime with Σ₂ ⸦ J⁺( Σ₁), and be H₁ = H∩Σ₁, H₂ = H∩Σ₂, where H denotes an event horizon. Then H₂≥ H₁.

The fact that astrophysical black holes are always immersed in the cosmic background radiation, whose temperature is much higher than the horizon temperature, implies that they always accrete and then, by the first law of black holes (^{Bardeen et al. 1973}), H₂ > H₁. The total area of black holes increases with cosmic time. The accretion should include not only photons but also charged particles. This means that the total number of charges in the causal past of any point pr→,t. will be different from their number in the corresponding causal future. This situation creates a local asymmetry that can be related to the Second Law. Figure 3 illustrates the setting.

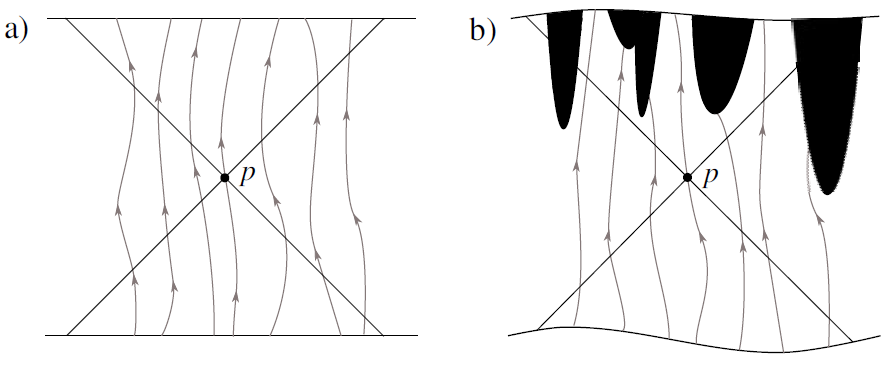
Figure 3 Sketch of the causal structure around a point pr→,t. in a) Minkowski spacetime, and b) a general relativistic spacetime with black hole formation. Vertical lines indicate worldlines of charges (sources). Black regions represent black holes. Charge densities are different in the causal past and the causal future. 

Let us now introduce a vector field L^μ given by:

If g_μvL^μT^v ≠ 0, with T^v = (1,0,0,0) there is a preferred direction for the Poynting flux in spacetime. The Poynting flux is given by:

where E→ and B→ are the electric and magnetic fields and TEMab is the electromagnetic energy-momentum tensor.

In a black hole interior the direction of the Poynting flux is toward the singularity. In an expanding, accelerating universe, it is in the global future direction. We see, then, that a timelike vector field, in a general spacetime (M , g ), can be anisotropic. There is a global to local relation given by the Poynting flux as determined by the curvature of spacetime that indicates the direction along which events occur. Physical processes, inside a black hole, have a different orientation from outside. At larger scales, the causal structure of the world is determined by the dynamics of spacetime and the initial conditions. Macroscopic irreversibility²⁶ and time anisotropy emerge from fundamental reversible laws.

There is an important corollary to these conclusions. Local observations about the direction of events can provide information about global features of spacetime and the existence of horizons and singularities (^{Romero et al. 2017}).

8. Black Holes and Supertasks

A supertask is an infinite sequence of actions that can be performed in a finite interval of time. The term "supertask" was introduced by Thomson in the 1950s in a famous paper (1954). The topic experienced a kind of revival after Pérez Laraudogoitia proposed a new kind of "beautiful supertask" (1996). This turned the discussion from the logical possibility to the physical implications of supertasks. Soon, black holes were invoked as instrumental for presumed demonstrations of the physical viability of supertasks and, in particular, for hyper-computation.

The expression "hyper-computing" refers to the actual performance of an infinite number of operations in a finite time with the aim of calculating beyond the ^{Turing barrier (1937)}. It has been suggested that such a hyper-computation can be performed in Kerr spacetimes (^{Németi and David 2006}, ^{Németi and Andréka 2006}). The Kerr spacetime belongs to the class of the so-called Malament-Hogarth (M-H) spacetimes. These are defined as follows (^{Hogarth 1994}):

DEFINITION. (M , g_ab) is an M-H spacetime if there is a future-(directed timelike half-curve γ ⸦ M and a point p ∈ M such that ∫γdτ=∞ and γ ⸦ J^-(p).

Here, τ denotes the proper time of the system that generates γ. The curve γ is the world-line of that physical system. Because this system has an infinite amount of time available, it may complete an infinite number of tasks. But, at every point in γ, it is possible to send a signal to the point p. This is because there always exists a curve γ' with future endpoint p which has finite proper time. We can think of γ as the "sender" and γ' as the "receiver" of a signal. In this way, the receiver may obtain knowledge of the result of an infinite number of operations in a finite time. This is simply a consequence of the "sender" having "all the time in the world" to perform the task.

In a Kerr spacetime this scheme can be arranged as follows. The "sender" is a spacecraft orbiting the Kerr black hole with a computer onboard. The "receiver" is a capsule ejected by the orbiter that falls into the black hole (think of David Bowman's pod jumping into the stargate in 2001: a Space Odyssey, but replace the stargate by a Kerr black hole). As the capsule approaches the inner horizon it intersects more and more signals from the orbiter, which emits periodically results of the computer calculations into the black hole. By the time the capsule crosses the inner horizon it has received all signals emitted by the computer in an infinite time (assuming that both the black hole and the orbiter can exist forever). This would allow the astronauts in the capsule to get answers to questions that require beyond-Turing computation! (^{Németi and David 2006}). The whole situation is depicted in Figure 4.

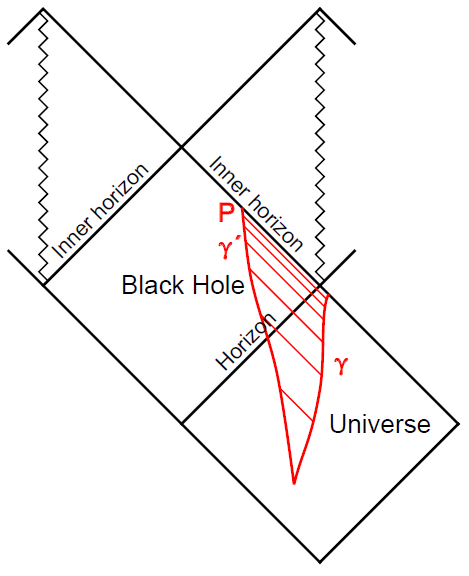
Figure 4 Carter-Penrose diagram of a Kerr black hole. The trajectories of two physical systems are indicated: γ remains in the exterior spacetime for an infinite amount of time, whereas γ' falls into the black hole. In the time it takes the latter to reach the inner horizon, the former arrives at the conformal infinity. The lines that connect both trajectories represent signals sent from γ to γ^'. 

There are many reasons to think that the described situation is physically impossible. I will mention the following ones: 1) The required inner black hole structure does not correspond to an astro-physical black hole generated by gravitational collapse. In a real black hole the Cauchy horizon is expected to collapse into a (probably null) singularity due to the backscattered gravitational wave tails that enter the black hole and are blueshifted at the Cauchy horizon (^{Brady 1999}). The instability of the Cauchy horizon seems to be a quite general feature of any realistic black hole interior model.²⁷ 2) The black hole is not expected to exist during an infinite time: it should evaporate through Hawking radiation, over a very long (but always finite) time. 3) The performance of infinite operations would require an infinite amount of energy. Even if the universe were infinite, a finite spacecraft cannot manipulate infinite amounts of energy. 4) If signals are periodically sent to the receiver, the blueshifted electromagnetic radiation would burn the capsule by the time it crosses the Cauchy horizon. ^{Németi and David (2006)} argue that this might be circumvented by sending just one signal with the final result. This suggestion faces the problems of the actual infinite: for any moment outside the black hole there will always be a further moment; when, then, the spaceship would send this signal? 5) The universe seems to be entering into a de Sitter phase, so particle horizons will appear and block part of the accessible spacetime to the spacecraft limiting its resources. Eventually the spacecraft itself would be engulfed by the cosmological horizon and its signals would stop arriving at probe inside the black hole.

I think that the cumulative argument is strong enough to support a hyper-computing avoidance conjecture: the laws of physics are such that no actual hyper-computation can be performed. Black holes do not offer any evident way of circumventing this conjecture. Rather, on the contrary, since any attempt to perform an actual supertask in nearly flat spacetime would required the release of an infinite amount of energy into a finite spacetime region, black holes should be formed as a consequence, violently cutting the execution of any superstask independently of the details of the "super-machine".²⁸

I conclude that it is pretty safe to say that no supertask can be accommodated in the real universe.

9. Black Holes and Presentism

Presentism is a metaphysical thesis about what there is. It can be expressed as (e.g. ^{Crisp 2003}):

Presentism. It is always the case that, for every x, x is present.

The quantification in this scheme is unrestricted, it ranges over all existents. In order to render this definition meaningful, the presentist must provide a specification of the term "present". Crisp, in the cited paper, offers the following definition:

Present. The mereological sum of all objects with null temporal distance.

The notion of temporal distance is defined loosely, but in such a way that it accords with common sense and the physical time interval between two events. From these definitions it follows that the present is a thing, not a concept. The present is the ontological aggregation of all present things. Hence, to say that "x is present", actually means "x is part of the present".

The opposite thesis of presentism is eternalism, also called four-dimensionalism. Eternalists subscribe the existence of past and future events. The temporal distance between such events is non-zero. The name four-dimensionalism comes from the fact that in the eternalist view, objects are extended through time, and then they have a 4-dimensional volume, with three spatial dimensions and one time dimension. There are different versions of eternalism.²⁹ The reader is referred to ^{Rea 2003} and ^{Romero 2017} for discussions of eternalism.

I maintain that presentism is incompatible with the existence of black holes. Let us see a simple, two-step argument against presentism based on some basic features of General Relativity that are particularly evident in the presence of black holes.³⁰

Argument A1:

Argument A2:

Simultaneity is frame-dependent. Since what exists cannot depend on the reference frame we use to describe it, we conclude that there are non-simultaneous events. Therefore, presentism is false.

Let us see which assumptions are open to criticism by the presentist.

A presentist might plainly reject P1. Although there is significant astronomical evidence supporting the existence of black holes (e.g. ^{Romero and Vila 2014} and references therein), the very elusive nature of these objects still leaves room for some speculations like gravastars and other exotic compact objects. The price of rejecting P1, however, is very high: black holes are now a basic component of most mechanisms that explain extreme events in astrophysics, from quasars to the so-called gamma-ray bursts, from the formation of galaxies to the production of jets in active galaxies and microquasars. The recent detection of gravitational waves from the merging of binary systems of black holes represents almost conclusive evidence for the existence of such objects. The presentist rejecting black holes should reformulate the bulk of contemporary high-energy astrophysics in terms of new mechanisms. In any case, P1 is susceptible of empirical validation through direct imagining of the supermassive black hole "shadow" by sub-mm interferometric techniques in the case of the nearby galaxy M87, something that was recently achieved, dispelling almost all doubts³¹ (^{Event Horizon Telescope (EHT) Collaboration 2019}).

The presentist might, instead, reject P2. After all, we know that General Relativity fails at the Planck scale. Why should it provide a correct description of black holes? The reason is that the horizon of a black hole is quite far from the region where the theory fails (the singularity). The distance, in the case of a Schwarzschild black hole, is r_s = 2GM/c². For a black hole of 20 solar masses, such as the one suspected to form part of the binary system Cygnus X-1, this means 60 km. And for the black hole in the center of our Galaxy, about 12 million km. Any theory of gravitation must yield the same results as General Relativity at such distances. So, even if General Relativity is not the right theory for the classical gravitational field, the correct theory should predict the formation of black holes under the same conditions.

There is not much to do with P4, since it follows from the condition that defines the null surface: ds = 0;³² similarly P4i only specifies one of the events on the null surface. A presentist might refuse to identify "the present" with a null surface. After all, in Minkowskian spacetime or even in a globally time-orientable pseudo-Riemannian spacetime the present is usually taken as the hyperplane perpendicular to the local time. But in spacetimes with black holes, the horizon is not only a null surface; it is also a surface locally normal to the time direction. In a Minkowskian spacetime the plane of the present is not coincident with a null surface. However, close to the event horizon of a black hole, things change. As we approach the horizon, the null surface matches the plane of the present. On the horizon, both surfaces are exactly coincident. A presentist rejecting the identification of the present with a closed null surface on an event horizon should abandon what is perhaps his or her most cherished belief: the identification of "the present" with hyper-surfaces that are normal to a local timelike direction.

The result mentioned above is not a consequence of any particular choice of coordinates but an intrinsic property of a black hole horizon. This statement can be easily proved. The symmetries of Schwarzschild spacetime imply the existence of a preferred radial function, r, which serves as an affine parameter along both null directions. The gradient of this function, ra=∇ar satisfies (c = G = 1):

Thus, r^a is spacelike for r > 2M, null for r = 2M, and timelike for r < 2M. The 3-surface given by r = 2M is the horizon H of the black hole in Schwarzschild spacetime. From Eq. (37) it follows that r^ar_a = 0 over H, and hence H is a null surface.³³

Premise P5, perhaps, looks more promising for a presentist last stand. It might be argued that events on the horizon are not simultaneous with any event in the external universe. They are, in a very precise sense, cut off from the universe, and hence cannot be simultaneous with any distant event. Let us work out a counterexample.

The so-called long gamma-ray bursts are thought to be the result of the implosion of a very massive and rapidly rotating star. The core of the star becomes a black hole, which accretes material from the remaining stellar crust. This produces a growth of the black hole mass and the ejection of matter from the magnetized central region in the form of relativistic jets (see, again, ^{Romero and Vila 2014} for astrophysical references). Approximately, one of these events occurs in the universe per day. They are detected by satellites such as Swift, with durations of a few tens of seconds. This is the time that takes for the black hole to swallow the collapsing star. Let us consider a gamma-ray burst of, say, 10 seconds. Before these 10 seconds, the black hole did not exist for a distant observer O1. Afterwards, there is a black hole in the universe that will last more than the life span of any human observer. Let us now consider an observer O2 collapsing with the star. At some instant he or she will cross the null surface of the horizon. This will occur within the 10 seconds that the collapse lasts for O1. But for O2 all photons that cross the horizon are simultaneous, including those that left O1 long after the 10 seconds from the event and crossed the horizon after traveling a long way. For instance, photons leaving the planet of O1 one million years after the gamma-ray burst, might cross the horizon, and then can interact with O2. So, the formation of the black hole is simultaneous with events in O1 and O2, but these very same events of O2 are simultaneous with events that are in the distant future of O1.

The reader used to working with Schwarzschild coordinates perhaps will object that O2 never reaches the horizon, since the approaching process takes an infinite time in a distant reference frame. This is, however, an effect of the choice of the coordinate system and the test-particle approximation.³⁴ If the process is represented in Eddington-Finkelstein coordinates, it takes a finite time for the whole star to disappear, as shown by the fact that the gamma-ray bursts are quite short events. Accretion/ejection processes, well-documented in active galactic nuclei and microquasars also show that the time taken to reach the horizon is finite in the asymptotically flat region of spacetime.

My conclusion is that black holes can be used to show that presentism provides a defective picture of the ontological substratum of the world. The whole argument, of course, is based upon the breakdown of absolute simultaneity in General Relativity. This breakdown is already present in Special Relativity, and has been widely used and discussed against presentists since the 1960s at least, e.g. ^{Smart 1963}, ^{Putnam 1967}, and ^{Stein 1968}.³⁵ The introduction of black holes only takes this breakdown of simultaneity to the extreme.

The recent detection of gravitational waves also provides a simple argument against presentism (^{Romero 2018a}):

P1. There are gravitational waves.

P₂. Gravitational waves have non-zero Weyl curvature.

P3. Non-zero Weyl curvature is only possible in 4 or more dimensions.

P₄. Presentism is incompatible with a 4-dimensional world.

Then, presentism is false.

The logic is sound, so let us review the premises of the argument to see whether there is some escape route for the presentist. The truth of P₁ is accepted by the vast majority of scientists working on gravitation. Gravitational waves are a basic prediction of General Relativity. The Laser Interferometer Gravitational Wave Observatory (LIGO) has directly detected gravitational waves from several merging black hole binary systems and even one neutron star merger (e.g. ^{Abbott et al. 2016a}, ^2016b). Indirect evidence for the existence of gravitational waves is known since long ago from the orbital decay of the binary pulsar PSR B1913+16, discovered by Hulse and Taylor in 1974. The decay of the orbital period of the binary system is in such accord with the predictions of General Relativity that both scientists were awarded the Nobel Prize in Physics 1993.³⁶ So, we can maintain that P1 is true on the basis of overwhelming empirical evidence.

Premises P₂ and P₃ are necessarily true. Gravitational waves propagate in empty space, where Einstein's field equations are reduced to:

This expression means that the 10 coefficients of the Ricci tensor are identically null. But the full Riemann tensor³⁷ has 20 independent coefficients since it is a rank 4 tensor. The remaining 10 components are expressed by the Weyl tensor. Then, since the gravitational waves are disturbances in the curvature of spacetime, the Weyl tensor must be non-zero in their presence. If the dimensionality of the world were such that it would have only 3 dimensions, as proposed by the presentists, the Riemann tensor would have only 6 independent components, and since in 3 dimensions Einstein's equations in vacuum are reduced to 6, the Weyl tensor must vanish. Only in 4 or more dimensions can gravity propagate through empty spacetime.³⁸

Then, the presentist should either deny that presentism is incompatible with 4-dimensionalism or accept that presentism is false. But presentism is essentially the doctrine that things do not have temporal parts (^{Heller 1990}). Any admission of temporal parts or time extension is tantamount to renouncing to the basic claim of presentism: there are no future or past events.

I conclude that presentism is utterly false.

10. Black Holes and Material Spacetime

Substantivalism is the doctrine that maintains the independent existence of space and time, which are considered to be material substances or even things or entities. Substantivalism, then, is ontological materialism about space and time. With the advent of General Relativity the ontological commitment shifted to spacetime. So, current substantivalism can be defined as the ontological doctrine which maintains that spacetime is an entity endowed with physical properties. This position is clearly expressed by ^{Einstein (1920)} and has been defended by many scientists and philosophers ever since.³⁹ I think that black hole astrophysics offers some fresh arguments for considering substantivalism true. But first, let us quickly review the old controversy.

Gottfried W. Leibniz and Isaac Newton famously argued about the nature of time and space in the seventeenth century. The controversy was developed with the participation of Samuel Clarke, who acted as the representative of Newtonian ideas (^{Leibniz and Clarke 2000}). Leibniz argued that space and time are not entities per se; that is, they do not exist in the absence of changing material objects. For Leibniz, space is just a system of spatial relations among objects, and time is a relationship among changing things. If nothing changes, Leibniz thought, there would be no time. If there were a single, unique object, there would be no space. For Newton, on the other hand, space and time were real entities, like tables or planets. However, unlike these, space and time are not affected by their interaction with the rest of the objects in the universe.

Leibniz developed an ingenious argument against Newton based on his principle of the identity of indiscernibles.⁴⁰ The argument is as follows: imagine two universes formed by exactly the same objects, related to each other in exactly the same way, but located in different spatial positions in otherwise empty spaces. If space is a thing, the spatial relationships among these objects will be very different, so the two universes will be different. However, there is no property in any of these two groups that allows us to distinguish them. Therefore, by the principle of the identity of indiscernibles, both universes are the same one. Since universes cannot be the same and still be different, one of the hypotheses must be rejected: 1) space is a thing; or 2) the principle of identity of indiscernibles. Leibniz thought we had reasons to agree with the second hypothesis and so, he negated the first one.

If space is not a physical entity as Newton thought, then what is it? Leibniz answers: a system of relationships among physical objects. There is no space, there are spatial relationships among existents. If there were no objects, there would be no space. If there were no changes, there would be no time.

Newton forcibly disagreed. In order to prove that space is something that exists independently of other things, he proposed the famous experiment of the bucket filled with water hanging from the ceiling by a rope.⁴¹ Turn it on itself, twisting the rope, and when you free it, the bucket will start spinning. At first, the surface of the water will be flat. Then, the bucket will start transmitting its rotating movement to the water through friction, and water will gain angular momentum. As momentum increases, the surface of the water will become parabolic due to centrifugal forces. If we stop the bucket, the water will keep rotating and it will maintain the parabolic surface until friction leaves it flat again.

With respect to what does the water accelerate? It cannot be accelerated with regard to the bucket, because the surface is parabolic whether the bucket rotates or not. Newton responded that it must be accelerated with regard to absolute space. So absolute space must be "something". It must have an ontological import. Nothing can accelerate with regard to nonexistent entities.

Unfortunately, Leibniz died during this controversy and could never offer a response to this argument. But Ernst Mach did in the nineteenth century:⁴² he claimed that water accelerates with respect to the "distant stars"; that is, with respect to the average of the remaining mass of the universe. Later, in the twentieth century, Einstein thought he could explain the nature of inertia and Mach's principle with his theory of General Relativity; he showed that gravitation and inertia are two aspects of the same gravito-inertial field, and thought that his theory would not admit solutions that do not include material objects. Einstein initially believed that space and time could not exist without matter.

In 1917, the Dutch astronomer Willem de Sitter obtained a dynamic solution of Einstein's equations that represents a universe without matter, but with dynamic empty space. Einstein was skeptical at first, but he later admitted that his theory was not useful for explaining Mach's principle. Worse, his theory represented the gravito-inertial field using a metric field and could effectively determine distances and other physical properties of spacetime, such as its energy density, in the absence of matter.

Is spacetime a physical entity? Does it really exist independently of other things? These questions might seem purely philosophical in nature, yet nevertheless, we can answer them through arguments based on black holes. Let us consider the following argument for the material⁴³ existence of spacetime (^{Romero 2017}):

P₁. Only material entities can be heated.

P2. Spacetime can be heated.

Therefore, spacetime is a material entity.

Premise P₁ is true. Heating is transmitting warmth to a physical system. It elevates the temperature of the system. That operation can only happen to physical systems, not to abstract systems or relationships among physical systems. P₂ is also true, in the light of relativistic physics:⁴⁴ the event horizon of a black hole has a temperature and this temperature changes when something falls through the horizon. If we can heat the horizon it is because we are heating spacetime (there is nothing else at the horizon but spacetime), and therefore spacetime exists materially.⁴⁵

We can formulate a similar argument based upon the concept of entropy.

P1. Spacetime has entropy.

P₂. Only things with a microstructure can have entropy.

Therefore, spacetime has a microstructure.

P₃. If something has a microstructure, it must exist.

Thus, spacetime exists.

P₁ is true because the event horizon of black holes is a region of spacetime with entropy (actually, most of the entropy of the universe is in the form of black holes.⁴⁶ Entropy measures the number of available microstates for a macroscopic system, and hence entropy can only be assigned to physical systems with a microstructure. From that, we conclude that spacetime is an existing material entity and not a mere system of relationships. Thus, we see that the existence of black holes has important philosophical consequences for the old metaphysical disputes about the existence of space and time.

Another argument, based on gravitational waves, has been proposed and discussed by ^{Bunge (2018)} and ^{Romero (2018b)}). The argument is as follows:

P₁. Gravitational waves activate detectors.

P2. Detectors react only to specific material stimuli.

P3. LIGO has detected gravitational waves.

Hence, gravitational waves are material.

P4. Gravitational waves are ripples of spacetime.

P5. Gravitational waves are material (first part of the argument).

Hence, spacetime is material.

In order to argue for P₄ let's consider Einstein's equations (1) once again.

They are a set of ten non-linear differential equations for the metric coefficients g_μv. T_μv is a second order tensor that represents the properties (energy-momentum) of all non-gravitational material fields. Einstein's equations establish a relation between some properties of spacetime (its curvature) and the properties of matter (energy density and momentum). Solving the equations, we get the metric of spacetime, we can calculate the connection formed by first order derivatives of g_μv, and then we obtain the equations of motion for test particles. If the curvature is different from zero, trajectories will depart from straight lines. If the test particle approximation cannot be ensured, the equations should be solved numerically through iterative methods in order to take into account the non-linearities. Notice that there is no gravitational field in this interpretation. There is just spacetime and matter.

To embrace the reality of spacetime is to accept that it is a material entity. This materiality is responsible for the non-linear nature of Einstein's theory. All kind of material entities can interact with spacetime through curvature, and this includes spacetime itself. In General Relativity, what we call "gravitational effects" are due to spacetime when its curvature is different from zero.

Although Einstein originally was inspired by Maxwell's and Lorentz's concepts of field, the final theory that resulted from his endeavor was not completely akin to Maxwell's. Einstein himself realized this after his famous debate with Willem de Sitter about the dynamics of empty universes.⁴⁷ Spacetime has a unique ontological status in General Relativity: it is an entity, which can exist by itself and, as LIGO detectors have shown, act upon matter. But spacetime can also exist in the absence of any other material entity. Einstein recognized the ontological status of spacetime in his address delivered on May 5th, 1920 in the University of Leiden: "Recapitulating, we may say that according to General Relativity space is endowed with physical qualities" (1920).

The gravitational field is alien to General Relativity in a similar way as classical concepts such as intrinsic angular momentum are alien to Quantum Mechanics. The theory, of course, can account for the phenomena we dub "gravitational" through the curvature of spacetime. But the ontological commitment is with spacetime, not with a classical scalar field for a gravitational force.

Any physically interpreted equation must equate symbols that represent the same ontological category of objects. In physics, what is usually represented in the equations are properties of material things. And this is exactly what EFEs do: on the left side we have a property of a system, curvature of spacetime, and on the right side we have another property: energy-momentum of physical systems, including spacetime.⁴⁸ The equations just establish how some properties (e.g. curvature) change if other properties (energy and momentum) evolve. The situation is quite similar to other fundamental equations of physics such as Maxwell's, where the intensity of the field changes if the currents change. In all cases, the ontological category of the referents remain the same in both sides of the equations. If spacetime were not material, its curvature would not be affected by changes in the distribution of mass and momentum of binary black holes systems, for instance.

11. Black Holes and Information

"Is information destroyed by black holes?" This is a question often heard in the popular scientific press and even in academic journals. The interest in this supposed problem is additionally sparked by the notorious changes of opinion of Stephen Hawking, a popular persona who was always at the center of public attention. In 1976 he answered the question by the positive (1976), and towards the end of his life by the negative (2015).

Most of the discussion of the so-called information paradox is misleading because of a lack of specification of the concept of information. What is, exactly, information? This word is a polysemic term. In ordinary usage it designates a property of languages (the propositional content of a signal). In this sense, there is no "law of conservation" of the information, nor it is true that information can never decrease. In fact, it may disappear, as anyone who has lost a hard disk can corroborate.

Some authors confuse "information" with "entropy", which is a thermodynamic concept. This confusion seems to come from J. von Neumann, who advised, not without some sarcasm, Claude Shannon to adopt the expression "entropy' to name the information characterized in the mathematical theory of communications developed by ^{Shannon and Weaver (1949)}:

You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, nobody knows what entropy really is, so in a debate you will always have the advantage. (^{Floridi 2010, p. 46}).

Shannon's information is a much more general concept than statistical thermodynamic entropy. Information "entropy" is present whenever there are unknown quantities that can be described only by a probability distribution. When some physicists write about a "Principle of Information Conservation" (e.g. ^{Susskind and Lindesay 2010}), what they really mean is that the entropy of an isolated system in equilibrium should not increase, since it already is at its maximum value. When a black hole accretes matter, however, the entropy increases (they say that "information is destroyed"). Even if the black hole finally radiates away the whole mass absorbed, the radiation will be thermal, so the entropy of matter will continue to increase.

As pointed out by Penrose, these considerations do not take into account the entropy of the spacetime. The state of maximum entropy of spacetime corresponds to the situation of gravitational collapse, which results in the formation of a black hole (^{Penrose 2010}). As the black hole evaporates, the entropy of the hole decreases. Eventually, after the black hole has completely evaporated, the radiation will be in thermal equilibrium and spacetime is in a maximally ordered state. After a huge amount of time, the universe might return to a state of minimum overall entropy. Black holes, in this sense, might act as some "entropy regeneration engines", restoring the initial conditions of the universe.

According to the level of confusion we can differentiate several alleged paradoxes regarding "information" and black holes. Let us briefly review them.

There are several possible solutions to this problem:

12. Black Holes, Singularities, and Quantum Spacetime

We have seen that black hole spacetimes are singular, at least in standard General Relativity. Moreover, singularity theorems formulated by ^{Penrose (1965)} and ^{Hawking and Penrose (1970)} show that this is an essential feature of black holes. Nevertheless, essential or true singularities should not be interpreted as representations of physical objects of infinite density, infinite pressure, etc. Since the singularities do not belong to the manifold that represents spacetime in General Relativity, they simply cannot be described or represented in the framework of such theory. General Relativity is incomplete in the sense that it cannot provide a full description of the gravitational behavior of some physical systems. True singularities are not within the range of values of the bound variables of the theory: they do not belong to the ontology of a world that can be described with 4-dimensional differential manifolds. Let us see this in more detail.⁵³

A spacetime model is said to be singular if the manifold M is incomplete. A manifold is incomplete if it contains at least one inextensible curve. A curve γ: [0, a) → M is inextensible if there is no point p in M such that γ(s) → p as a → s, i.e. γ has no endpoint in M. A given spacetime model M, g has an extension if there is an isometric embedding θ: M → M', where M', g' is another spacetime model and θ is an application onto a proper subset of M'. A singular spacetime model contains a curve γ that is inextensible in the sense given above. Singular spacetimes are said to contain singularities, but this is an abuse of language: singularities are not "things" in spacetime, but a pathological feature of some solutions of the fundamental equations of the theory.

Singularity theorems can be proved from pure geometrical properties of the spacetime model (^{Clarke 1993}).⁵⁴ The most important of these theorems is due to ^{Hawking and Penrose (1970)}:

THEOREM. Let M, g be a time-oriented spacetime satisfying the following conditions:

Then, M, g contains at least one incomplete timelike or null geodesic.

If the theorem has to be applied to the physical world, the hypothesis must be supported by empirical evidence. Condition 1 will be satisfied if the energy-momentum T^μv satisfies the so-called strong energy condition: TμvVμVv≥-1/2Tμμ, for any timelike vector V^μ. If the energy-momentum is diagonal, the strong energy condition can be written as ρ + 3p ≥ 0 and ρ + p ≥ 0, with ρ the energy density and p the pressure. Condition 2 requires that any timelike or null geodesic experiences a tidal force at some point in its history. Condition 4a requires that, at least at one time, spacetime is closed and the compact slice that corresponds to such a time is not intersected more than once by a future directed timelike curve. The trapped surfaces mentioned in 4b refer to surfaces inside the (outer) horizons, from where congruences focus all light rays on the singularity. Condition 4c requires that the space is collapsing in the past or the future. Astrophysical black holes formed through gravitational collapse are expected to satisfy these conditions.⁵⁸

I insist, the theorem is purely geometric, no physical law is invoked. Theorems of this type are a consequence of the focusing of congruences.

Singularity theorems are not theorems that imply physical existence, under some conditions, of spacetime singularities. Material existence cannot be formally implied. Existence theorems imply that under certain assumptions there are functions that satisfy a given equation, or that some concepts can be formed in accordance with some explicit syntactic rules. Theorems of this kind state the possibilities and limits of some formal system or language. The conclusions of the theorems, although not obvious on many occasions, are always a necessary consequence of the assumptions made.

In the case of singularity theorems of classical field theories like General Relativity, what is implied is that under some assumptions the solutions of the equations of the theory are defective beyond repair. The correct interpretation of these theorems is that they point out the incompleteness of the theory: there are statements that cannot be made within the theory. In this sense (and only in this sense), the theorems are like Gödel's famous theorems of mathematical logic.⁵⁹

To interpret the singularity theorems as theorems about the existence of certain spacetime models which contain singularities is wrong. Using elementary second order logic is trivial to show that there cannot be non-predicable objects (singularities) in the theory (^{Romero 2013b}). If there were a non-predicable object in the theory,

where the quantification over properties is unrestricted, i.e. P stands for any property. The existential quantification ∃xE, on the other hand, means

where E is some set of objects admitted within the theory.

Let us call P₁ the property "x ∈ E". Then, formula (40) reads:

which is a contradiction, i.e. it is false for any value of x.

I conclude that cannot exist a material entity such as a singularity. There is just a theory with a restricted range of applicability.

The reification of singularities can lead us to accept an incredible ontology. We read, for instance, in a book on foundations of General Relativity:

[…] a physically realistic spacetime must contain such singularities. […] there exist causal, inextensible geodesics which are incomplete. […] If a geodesic cannot be extended to a complete one (i.e. if its future endless continuation or its past endless continuation is of finite length), then either the particle suddenly ceases to exist or the particle suddenly springs into existence. In either case this can only happen if spacetime admits a "singularity" at the end (or the beginning) of the history of the particle. (^{Kriele 1999, p. 383})

This statement and many similar ones found in the literature commit the elementary fallacy of confusing a model with the object being modeled. Spacetime does not contain singularities. Some of our spacetime models are singular. It is this incomplete character of the theory that prompt us to go beyond General Relativity in order to get a more comprehensive view of the gravitational phenomena. Objects falling into a black hole do not "suddenly cease to exist" in their interior, as shown by the fact that the mass of the black hole increases with the accretion of matter. As was very clear to Einstein, his general theory breaks down when the gravitational effects of quantum objects start to affect spacetime. Then, the theory cannot be used to describe the state and evolution of physical systems when such a regime is reached.

Whatever the state of matter is at the center of black holes, it is something different from what we know. If spacetime is to remain always a continuum then the gravitational collapse should stop before the Planck scale. This would require a violation of the energy conditions according to the singularity theorems. In such a scenario the interior of a black hole would be mostly vacuum spacetime with a central region where a central object would be located (at least in the absence of rotation). The overall picture is known as a regular black hole. Such objects, if they exist, have a very peculiar thermodynamic behavior in their interiors (^{Pérez et al. 2011a}).

Alternatively, the core of the black hole might be a kind of condensate of quantum spacetime. There are several approaches to quantum spacetime, including quantum-loop gravity and causal sets. An overview of such proposals is well beyond the scope of the present work. The interested reader might want to turn to the papers by ^{Oriti (2014)}, ^{Dowker (2006)}, ^{Romero (2017)} and the book by ^{Rovelli (2004)}.

Another interesting feature of black hole interiors is the existence, according to the steady-state theory, of a region with closed timelike curves (CTCs) in Kerr and Kerr-Newman black holes. This is the region interior to the second horizon; chronology violation is generated by the tilt of the light cones around the rotation axis in this part of spacetime (e.g. ^{Andréka, Németi, and Wüthrich 2008}). The interior event horizon is also a Cauchy horizon. It is impossible to predict the evolution of any system inside the Cauchy horizons, as we have seen in section 6; these horizons are an indication of the breaking of predictability in the theory. They exhibit, however, highly pathological behavior; small time-dependent perturbations originating outside the black hole undergo an infinite gravitational blueshift as they evolve towards the horizon. This blueshift of infalling radiation gave the first indications that these solutions may not describe the generic internal structure of real black holes. ^{Simpson and Penrose (1973)} pointed this out more than 40 years ago, and since then linear perturbations have been analyzed in detail. ^{Poisson and Israel (1990)} showed that a scalar curvature singularity forms along the Cauchy horizon of a charged, spherical black hole in a simplified model. This singularity is characterized by the exponential divergence of the mass function with advanced time. The key ingredient producing this growth of curvature is the blueshifted radiation flux along the inner horizon.⁶⁰ Since then, the result was generalized to Kerr black holes (e.g. ^{Brady and Chambers 1995}, ^{Hamilton and Polhemus 2011}). These, and other results about the instability of the Kerr black hole interior, suggest that CTCs actually do not occur inside astrophysical black holes.

13. Cosmological Black Holes

Black hole solutions as those described in section 3 represent stationary regions in a static background spacetime. The real universe, however, is expanding. Moreover, it seems to expand in an accelerated way. Since both the black hole and global spacetime are expanding, this expansion should be taken into account in the description of the black hole, at least on long timescales.

The assumption of an expanding homogeneous and isotropic space-time leads to the Friedman-Lemaitre-Robertson-Walker (FLRW) metric:⁶¹

where t is the co-moving (with the cosmic fluid) time, a(t) is a scale factor, and k is a normalized curvature index whose values are 0, +1, or -1 for flat, positively, and negatively curved spatial sections of the universe.

^{McVittie (1933)} was the first to combine a Schwarzschild solution with an FLRW background metric to find the effects of the expanding universe on a massive object. McVittie metric is based on the following assumptions: 1) at large distances from the compact object the metric is given approximately by the FLRW expression, 2) when the expansion is ignored (i.e. when the scale factor of the universe a(t) = a₀ is constant), Schwarzschild metric is recovered, 3) the metric must be a consistent solution to Einstein's field equations with a perfect fluid energy-momentum tensor, and 4) there is no matter infall.

McVittie metric, with the assumption that the mass of the black hole increases with the scale factor a(t) in the form M_BH(t) = M₀a(t), reads (for a flat universe),

It is not trivial to show that this metric represents a black hole. The metric (43) presents two horizons, both of them dynamical; one is a trapping horizon, and the other one a cosmological horizon. Contrary to Schwarzschild metric, however, the horizon at r = M₀/2a(t) is singular, corresponding to a divergent pressure.⁶² The interpretation of this singularity has been under debate for some time, but it is clear that it corresponds to the event horizon from which the background fluid cannot escape. Most authors agree that the McVittie solution is only valid for r > M₀/2a(t).

There are several interesting features of this cosmological solution and its generalizations for other prescriptions of M(t). First, these metrics are not vacuum solutions. There is a cosmological fluid in the background spacetime, and the putative black hole accretes this fluid. Second, as the universe expands (or contracts in the time-reverse case) the black hole area increases (or decreases). This implies changes in the entropy of the black hole and interactions with the environment that are still not well understood. And then there is the curious feature that an object gravitationally bound to the black hole cannot describe a circular orbit. The reason is the expansion of the universe as the object moves around the black hole: the object never arrives back at the same point in space. This has been investigated in some detail by ^{Pérez et al. (2019)}.

There is another interesting consequence of the cosmological expansion. A force that pulls away the orbiting object naturally appears and increases with the expansion velocity (^{Nandra et al. 2012}, ^{Pérez et al. 2019}). In a universe with accelerated expansion and a cosmological horizon, there will be a time, in the far future, where everything except the orbiting object would be causally disconnected from the black hole. Nevertheless, the pull outwards will continue to increase. The origin of this force is neither in the black hole nor in the orbiting object. Since at this stance there will be nothing else acting upon the system, the only possible source of the force is the expansion of space. The philosophical implication is immediate: if space can exert a physical force upon a physical object, it must be material. Hence, a new argument for substantivalism appears in this cosmological context. A kind of Newton's bucket Gedankenexperiment, but this time without the possibility of appealing to distant stars or any other body to save relationism.

So far little is known about a Kerr metric embedded in an FLRW spacetime (^{Vaidya 1977}, ^{Guha Thakurta 1981}), and little is also known of the properties of spherically symmetric black hole solutions in more complex evolving universes. Currently, there is an ongoing investigation of the evolution of black holes through a cosmological bounce from a previous contracting phase of the cosmos. Such researches might shed some light on some pressing issues related to the physical processes in the early universe.⁶³

14. The Ontological Status of Black Holes

Current physics informs us that the world seems to be ultimately made up of a number of fields existing in spacetime. The Standard Model includes 6 lepton fields and 6 quark fields (and the corresponding anti-fields), plus several boson fields: the Higgs boson, the photon, 3 electroweak massive bosons (Z and W^±), and 8 gluons. So, altogether, we might say there are at least⁶⁴ 25 fields in nature.⁶⁵ These fields are extended over spacetime and, as far as we can say, they are simple, i.e. they do not have parts in a mereological sense. The composition of each of these fields seems to be the empty set.⁶⁶

The basic fields of the Standard Model are the closest thing to the classic idea of a substance you can get from current physics. They are simple existents that do not depend, as far as we can tell, on anything else. Simple existents are usually called "substances". The concept of substance has a long tradition in Western philosophy, from Aristotle to Locke and Spinoza.⁶⁷ If a substance exists, it should exist in some way or other. We call these ways properties. Substances and properties are complementary and inseparable. There are no such things as bare substances or independently existing properties. Properties are just modes of substances (^{Heil 2012}), the ways substances are. We separate them only by abstraction. Properties cannot exist by themselves, without a substance, in a similar way as a smile cannot exist without a face. A smile is just a certain arrangement of the various features that conform a face. In the world there are just smiling faces, not both smiles and faces. Properties are not parts of substances, or things somehow attached to substances. They are just the way substances are. Similarly, a substance cannot fail to be in some way or another; substances are always propertied.

As we have seen in section 5, fields can be excited. We call these excitations particles. Particles are modes of the fields. Charge, spin, rest mass, and other features we ascribe to particles are not properties of properties, or second-order properties, but just ways the properties are, i.e. the properties themselves. Unexcited fields are not unpropertied, since even a fundamental field is subjected to quantum fluctuations and has specific symmetries and other properties.⁶⁸ Moreover, the vacuum state of a field is not relativistically invariant (^{Davis 1975}, ^{Unruh 1976}), so different detectors can measure different numbers of particles or excitations.

Fields interact and form more or less stable and dynamical configurations that we identify with the manifold objects we find in the world. Atoms, people, planets, stars, galaxies: all of them are made of interacting fields.

Black holes do not seem to fit in this scheme. They can interact with fields and complex objects formed by them, but they do not seem to be formed by fields. The event horizon that separates space-time delimiting the region we call a black hole is not a substance akin to those that constitute other material objects. And nevertheless, a black hole can interact with material objects such as stars, even tearing them apart. Magnetic fields can be twisted by rotating black holes and help to launch powerful jets of particles. How is this possible if black holes are not as material as the objects and fields they affect?

To answer this we first need some criteria for materiality. If something is material, that something should exist independently of our representations. Many properties change if we change our representation of them. Some of them can even disappear through changes of reference frames and even through changes of coordinates within the same reference system. The only universal property that cannot be fully removed through a global change of representation is energy. Energy is the capacity of a physical system to do work, i.e. to change the state of other systems. We call a particular object material if it has energy, if it can change and induce changes to other things.⁶⁹ Numbers, sets, fictional characters, and the like do not have energy, they cannot change, they exist only fictionally as parts or terms in conceptual systems. Hence we do not attribute them independent material existence, but just conceptual existence relative to some context.⁷⁰ Black holes, according to this view, are fully material because they can do work on other material systems.

However, a black hole is just a region of spacetime with some particular curvature. Although they are usually thought to be formed in astrophysics from the collapse of other objects constituted by fields (e.g. massive stars), this is not an essential feature. They might also result from strong fluctuations in spacetime itself. Their capacity to affect other systems is based on the curvature of spacetime. Space-time exerts work also through gravitational waves that result from metric (tensor) perturbations. The conclusion seems to be that a black hole is not a kind of substance being in some ways, but a mere mode of a substance, a specific way a substance, spacetime, is. Space-time can be in different ways. One way is what we call a black hole.

In this view, black holes are not like stars: entities formed by complexly intermingled substances existing in spacetime. They are something more basic: modes of existence of spacetime itself.

Spacetime is material because it has energy. But is not completely akin to the other fields of nature. Spacetime is more basic because it can exist without other fields. On the contrary, no field can exist without spacetime. To see this, let us just think of energy, which is represented by the energy-momentum tensor. For any field described by a Lagrangian density L, this tensor reads (e.g. ^{Romero and Vila 2014}):

We see that this physical quantity cannot be defined without the previous assumption of the existence of a spacetime with some metric structure (g^μv). On the contrary, spacetime does not need matter to exist; its own energy-momentum content does not necessarily depend on the matter fields (^{Lehmkuhl 2011}).

If the contents of the world can be summarized in the title of a famous book by H. ^{Weyl (1922)}, "space, time, and matter", we should ascribe black holes to the first part of this formula: spacetime. Whether spacetime and matter fields are just two different species of a more basic material substance is something that should be the subject of further investigations. The super-substantivalist program, once embodied by Wheeler's geometrodynamics, attempts at demonstrating that all fields can be understood, ultimately, as other manifestations of spacetime (^{Schaffer 2009}, ^{Lehmkuhl 2018}). Whether the most fundamental ontology of the world is this way or not is far from clear.

15. Conclusions

I have overviewed some philosophical problems related to black holes. The interface between black hole physics and philosophy remains mostly unexplored, and the list of topics I have selected here is by no means exhaustive. The study of black holes can be a very powerful tool to shed light on many other issues in the philosophy of science and ontology. Evolving black holes, black hole dependence of the asymptotic behavior of spacetime, the nature of inertia, the energy of gravitation, quantum effects in the near-horizon region, turbulent spacetime during black hole mergers, the classical characterization of the gravitational field, and regular black hole interiors are all physical topics that have philosophical significance. In black holes our current representations of space, time, and gravity are pushed to their very limits. The exploration of such limits can pave the way to new discoveries about the world and our ways of representing it. Discoveries in both science and philosophy.⁷¹