PACS: 25.80.Dj; 11.80.-m; 24.10.Ht
1. Introduction
Due to the mechanism of pion-nucleon interaction, with the pion’s mean free path associated with the pion’s incident kinetic energy
In region I, the pion is the best and most sensitive probe of spatial distributions in a nucleus. The pion is spinless; and it penetrates deeply inside the nucleus because pion-nucleon two-body interaction is weak. In fact, it is one of the most penetrating of the strongly interacting particles. Also it is a preferred probe, compared to the proton, as no need to make antisymmetrization with the nucleons inside a nucleus. In addition, it is the best spectroscopic tool to investigate the many overlapping resonances that do exist. Nevertheless, the presence of unconventional phenomena as mesonic current contributions and modified nucleon properties in the medium could be tested2.
In region II, the pion’s mean free path is small and it is comparable to the inter-nucleon distance3. So the pion is completely absorbed at the surface of the target nucleus, i.e. the scattering involves the nuclear surface. As such, the pion is an adequate probe for gleaning important nuclear peripheral information.
To facilitate the study of region III, it has been subdivided into two energy sub-regions: (III-a) the transition energy region,
Recently we have analyzed low-energy pion-nucleus elastic scattering data using a suggested scaling method, based on the results of the inverse scattering theory using available phase shifts for both
In Sec. 2, theory is briefly overviewed. In Sec. 3, results and discussion are presented. In the last section, Sec. 4, the conclusions are summarized.
2. Theory
This work is a continuation to our recent work5,7, and, as such, the theoretical background and theoretical relations are as already outlined and discussed before. Accordingly, a brief overview is provided here for completeness.
The potential adopted here,
The analytical form of the nuclear part is given by :
where the three terms are the attractive Woods-Saxon (WS), the repulsive Squared Woods-Saxon (SWS), and the surface Woods-Saxon, respectively. The Coulomb term,
which represents the interaction between a point charge, i.e. the incident charged pion, and a uniformly insulating charged sphere, i.e. the target nucleus of atomic number
To achieve our goals in obtaining differential and reaction cross sections,
with
All potential quantities, constants and scaled potential parameters, appearing explicitly or implicitly in the above equations are substituted by their numerical values. For emphasis, the quantities E, m,
It is well-know that the phase shift,
where
where
with the dimensionless parameter
Also
where
The determination of
where
where
3. Results and Discussion
As pointed out in our previous work2,5,7, the scaling method has been successful in obtaining the correct potential parameters capable of providing nice agreements between theory and experiment for alpha-nucleus11 and nucleus-nucleus12,13 nuclear systems. In addition, the scaling method is supported by Energy-Density Functional (EDF) theory13. Recently it has been also successful in determining the correct potential parameters for pion-nucleus systems in the low energy region. The extent of success, strength, capability and reliability of the scaling method are examined, here, by explaining the elastic-scattering angular distributions data for the pion-nucleus systems under consideration, namely
Based on our previous successful results, and guided by the corresponding obtained scaling relations, we are following the same strategy in determining the potential parameters and in obtaining the associated scaling relations for systems under investigation. The six potential parameters,
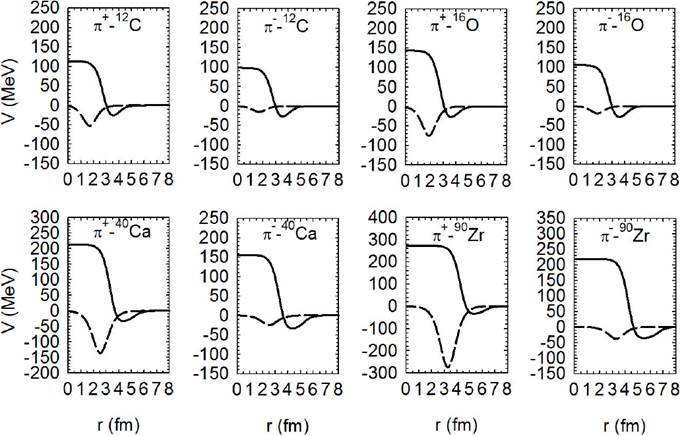
Figure 1 The real and imaginary parts of the scaled potentials, drawn as solid and dashed lines, respectively, used in analyzing

Figure 2 Same as Fig. 1 but for 30 MeV. The inverted real and imaginary potential points, obtained from available phase shifts14,15, are represented by solid circles and empty triangles, respectively.

Figure 4 The calculated differential cross sections, drawn as solid and dashed lines for positive and negative pions, respectively, compared to the experimental data, represented by solid circles and empty triangles16,17, as a function of center of mass angle θc.m. for 20 MeV incident charged pions scattered off the nuclei 12C, 16O, 40Ca, and 90Zr. The calculations are made by using the scaled potentials, real and imaginary parts, drawn as solid and dashed lines in Fig. 1 for both positive and negative pions, respectively.
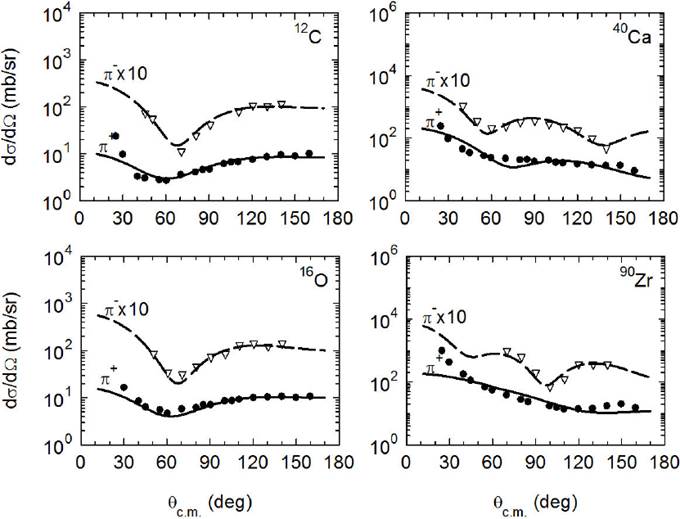
Figure 5 The calculated differential cross sections, drawn as solid and dashed lines for positive and negative pions, respectively, compared to the experimental data, represented by solid circles and empty triangles18,19, as a function of center of mass angle θc.m. for 30 MeV incident charged pions scattered off the nuclei 12C, 16O, 40Ca, and 90Zr. The calculations are made by using the scaled potentials, real and imaginary parts, drawn as solid and dashed lines in Fig. 2 for both positive and negative pions, respectively.

Figure 6 The calculated differential cross sections, drawn as solid and dashed lines for positive and negative pions, respectively, compared to the experimental data, represented by solid circles and empty triangles17,20,21, as a function of center of mass angle θc.m. for 40 MeV incident charged pions scattered off the nuclei 12C, 16O, 40Ca, 58Ni and 90Zr. The calculations are made by using the scaled potentials, real and imaginary parts, drawn as solid and dashed lines in Fig. 3 for both positive and negative pions, respectively.
Table I The optical potential parameters R0 (in fm), V1 (in MeV), W3(in MeV), R1(in fm), R3(in fm) and a3(in fm) used in Eq. (2) for 20 MeV incident charged pions on target nuclei noted in column one. Other optical potential parameters, given in Eq. (2), are kept fixed with the values V0 = -37.0 MeV, a0 = 0.324 fm and a1 = 0.333 fm. Our calculated reaction cross sections, σr (theor) in millibarns, for both π+ and π- , are listed in columns 8.
| Nucleus | R0 | V1 | W3 | R1 | R3 | a3 | σr (theor) | ||||
| π+ | π- | π+ | π- | π+ | π- | π± | π+ | π- | |||
| Carbon-12 | 4.00 | 4.03 | 150.0 | 140.0 | -210.0 | -70.0 | 3.00 | 1.70 | 0.370 | 100.4 | 227.4 |
| Oxygen-16 | 4.15 | 4.18 | 180.0 | 142.0 | -300.0 | -75.0 | 3.00 | 1.87 | 0.370 | 123.1 | 360.4 |
| Silicon-28 | 4.70 | 4.75 | 214.0 | 171.0 | -400.0 | -83.0 | 3.25 | 2.25 | 0.420 | 248.4 | 641.7 |
| Sulfur-32 | 4.82 | 4.92 | 223.0 | 179.0 | -444.0 | -88.0 | 3.25 | 2.36 | 0.420 | 324.6 | 754.3 |
| Calcium-40 | 5.20 | 5.30 | 250.0 | 193.0 | -543.0 | -100.0 | 3.54 | 2.54 | 0.420 | 345.4 | 842.6 |
| Iron-56 | 5.45 | 5.74 | 267.0 | 218.0 | -680.0 | -107.0 | 3.85 | 2.84 | 0.420 | 381.4 | 1003.0 |
| Nickel-58 | 5.54 | 5.80 | 271.0 | 221.0 | -742.0 | -118.0 | 3.92 | 2.86 | 0.420 | 405.1 | 1004.7 |
| Zirconium-90 | 6.20 | 6.25 | 310.0 | 256.0 | -1100.0 | -150.0 | 4.50 | 3.30 | 0.420 | 494.4 | 1129.6 |
Table II The optical potential parameters R0 (in fm), V1 (in MeV), W3(in MeV), R1(in fm), R3(in fm) and a3(in fm) used in Eq. (2) for 30 MeV incident charged pions on target nuclei noted in column one. Other optical potential parameters, given in Eq. (2), are kept fixed with the values V0 = -37.0 MeV, a0 = 0.324 fm and a1 = 0.333 fm. Our calculated reaction cross sections, σr (theor) in millibarns, for both π+ and π- , are listed in columns 8.
| Nucleus | R0 | V1 | W3 | R1 | R3 | a 3 | σ r (theor) | ||||
| π+ | π- | π+ | π- | π+ | π- | π± | π+ | π- | |||
| Carbon-12 | 3.85 | 3.95 | 129.0 | 110.0 | -120.0 | -72.0 | 3.00 | 1.70 | 0.370 | 107.1 | 169.5 |
| Oxygen-16 | 4.00 | 4.10 | 155.0 | 122.0 | -175.0 | -84.0 | 3.00 | 1.87 | 0.370 | 137.1 | 256.3 |
| Silicon-28 | 4.55 | 4.69 | 185.0 | 147.0 | -245.0 | -111.0 | 3.25 | 2.25 | 0.420 | 278.6 | 473.4 |
| Sulfur-32 | 4.64 | 4.82 | 194.0 | 154.0 | -276.0 | -122.0 | 3.25 | 2.36 | 0.420 | 347.0 | 563.9 |
| Calcium-40 | 5.11 | 5.20 | 210.0 | 166.0 | -340.0 | -140.0 | 3.54 | 2.54 | 0.420 | 393.0 | 634.2 |
| Iron-56 | 5.14 | 5.48 | 236.0 | 186.0 | -458.0 | -180.0 | 3.85 | 2.84 | 0.420 | 426.0 | 769.3 |
| Nickel-58 | 5.20 | 5.56 | 239.0 | 188.0 | -479.0 | -193.0 | 3.92 | 2.86 | 0.420 | 435.9 | 774.1 |
| Zirconium-90 | 5.70 | 6.25 | 277.0 | 217.0 | -720.0 | -280.0 | 4.50 | 3.30 | 0.420 | 503.3 | 961.0 |
Table III The optical potential parameters R0 (in fm), V1 (in MeV), W3(in MeV), R1(in fm), R3(in fm) and a3(in fm) used in Eq. (2) for 40 MeV incident charged pions on target nuclei noted in column one. Other optical potential parameters, given in Eq. (2), are kept fixed with the values V0 = -37.0 MeV, a0 = 0.324 fm and a1 = 0.333 fm. Our calculated reaction cross sections, σr (theor) in millibarns, for both π+ and π- , are listed in columns 8.
| Nucleus | R0 | V1 | W3 | R1 | R3 | a3 | σr (theor) | ||||
| π+ | π- | π+ | π- | π+ | π- | π± | π+ | π- | |||
| Carbon-12 | 3.75 | 3.95 | 103.0 | 90.0 | -77.0 | -74.0 | 3.00 | 1.70 | 0.370 | 127.3 | 141.4 |
| Oxygen-16 | 3.89 | 4.05 | 125.0 | 100.0 | -110.0 | -96.0 | 3.00 | 1.87 | 0.370 | 170.7 | 201.6 |
| Silicon-28 | 4.33 | 4.59 | 154.0 | 123.0 | -178.0 | -134.0 | 3.25 | 2.25 | 0.420 | 313.7 | 393.9 |
| Sulfur-32 | 4.43 | 4.73 | 162.0 | 128.0 | -203.0 | -151.0 | 3.25 | 2.36 | 0.420 | 385.5 | 471.3 |
| Calcium-40 | 4.75 | 4.95 | 180.0 | 138.0 | -245.0 | -170.0 | 3.54 | 2.54 | 0.420 | 403.3 | 519.4 |
| Iron-56 | 4.93 | 5.43 | 199.0 | 156.0 | -351.0 | -234.0 | 3.85 | 2.84 | 0.420 | 505.1 | 678.6 |
| Nickel-58 | 5.00 | 5.52 | 200.0 | 160.0 | -366.0 | -250.0 | 3.92 | 2.86 | 0.420 | 512.6 | 683.2 |
| Zirconium-90 | 5.55 | 6.20 | 235.0 | 180.0 | -563.0 | -395.0 | 4.50 | 3.30 | 0.420 | 633.8 | 878.0 |
Our results show clearly that scaled potential parameters depend mainly on the incident pion’s kinetic energy,

Figure 7 The cube of R0-values versus the atomic mass of the target nucleus in atomic mass units, A(u) for Tπ = 20, 30, 40 MeV and 50 MeV. The R0-values at 50 MeV are taken from Ref. 7. The solid and dashed lines, for positive and negative pions, respectively, are just to guide the eye.

Figure 8 The cube of V1-values versus the atomic mass of the target nucleus in atomic mass units, A(u) for Tπ = 20; 30, 40 and 50 MeV. The V1-values at 50 MeV are taken from Ref. 7. The solid and dashed lines, for positive and negative pions, respectively, are just to guide the eye.
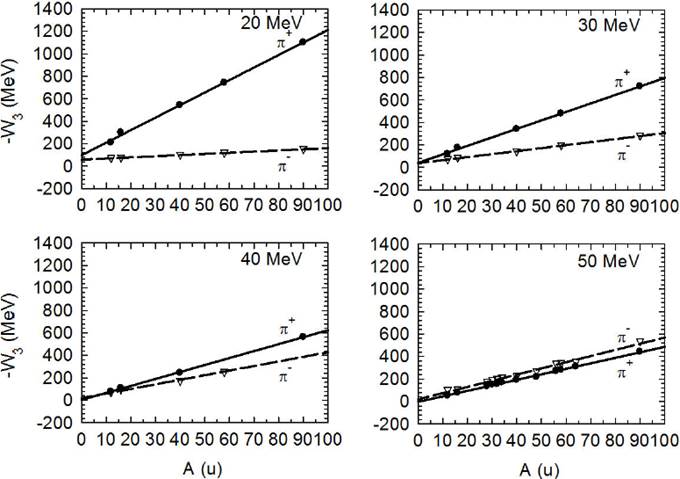
Figure 9 The W3-values versus the atomic mass of the target nucleus in atomic mass units, A(u) for Tπ = 20, 30, 40 and 50 MeV. The W3-values at 50 MeV are taken from Ref. 7. The solid and dashed lines, for positive and negative pions, respectively, are just to guide the eye.

Figure 10 The R0-values versus the incident pion’s kinetic energy, Tπ (MeV) for five different target nuclei. The R0-values at 50 MeV are taken from Ref. 7. The solid and dashed lines are just to guide the eye.

Figure 11 The V1-values versus the incident pion’s kinetic energy, Tπ (MeV) for positive pions scattered off five different target nuclei. The V1-values at 50 MeV are taken from ref.7. The solid and dashed lines are just to guide the eye.

Figure 12 The W3-values versus the incident pion’s kinetic energy, Tπ (MeV) for five different target nuclei. The W3-values at 50 MeV are taken from Ref. 7 and the W3-values at energies greater than 50 MeV are extrapolated.. The solid and dashed lines are just to guide the eye.
For positive pions with
and for negative pions with
For positive pions, the obtained scaling relations for the three potential parameters with the pion’s incident kinetic energy, for the five target nuclei under consideration, are, respectively :
4. Conclusions
This study confirms the suitability of the scaling method in obtaining potential parameters for a certain pion-nucleus system from a nearby one. This method is unique for low-energy pion-nucleus systems with no available shifts. The good agreements between calculated and measured differential cross sections, for different pion-nucleus systems at three low energies, represent a strong indication on the success of the method. Nevertheless, the analytical forms of our potentials agree with the inverted potential points where available. On the otherhand, and even with no available experimental reaction cross sections for most of the cases under consideration, or uncertain values for few of them, our calculated values are included, pending for future measured precise values. We believe that the results of this study, accompanied with the results of our two recent related studies, based on the scaling method are suitable to be submitted for a patent. In view of this, our scaling method will be used in analyzing low-energy kaon-nucleus elastic-scattering data. It is also tempted that this study, especially at 20 MeV, will positively contribute in accounting for pionic atom data and, then, in investigating pionic atom physics.











 nueva página del texto (beta)
nueva página del texto (beta)



