1. Introduction
Electron collisions with NH3 molecule are of prime interest in atomic and molecular processes in chemical reactions, collisions physics, interstellar space, atmosphere, radioactivity, plasmas (plasma etching, plasma deposition), switching device 1,2, biological matter and medicine. Ammonia is a colorless gas with a characteristic pungent smell; it is found in trace quantities in nature, being produced from the nitrogenous animal and vegetable matter, throughout the solar system, and in small quantities in rainwater. Ammonia is also known as caustic and hazardous in its concentrated form; it is currently used as fertilizer, cleaner, fuel, antimicrobial agent for food production, in fermentation, and textile. In addition, NH3 is one of the important molecules considered as a source of nitrogen atoms for the fabrication of nitride films and other nitrogen compounds 3. Considering these different domains of use, the e-NH3 interaction has been the subject of many investigations in various energy ranges theoretically as well as experimentally.
On the experimental side, the absolute cross section of e-NH3 interaction was measured first by Brüche in 1929 below 50 eV, using a Ramsauer-type apparatus 4, and then followed by the differential cross section (DCS) measurements reported by Harshbarger et al. (1971) 5 versus the momentum transfer between 2o-10o for 300, 400, and 500 eV, mentioning also unpublished data of Bromberg 6. The measurements of the total cross sections (TCS) on NH3 are renewed in 1987 by Sueoka et al. 7 using a linear transmission type time-of-flight apparatus from low to intermediate impact energies (0.7-400 eV). We also found the data reported by Szmytkowski et al. (1989) for impact energy from 1 to 80 eV, using a non-magnetic linear transmission technique 8. Particularly, the results show a very broad hump centered around 10 eV. At the same time, Pritchard et al. 9 mentioned that Shyn has measured the relative DCSs for e-NH3 interactions at 8.5 eV and 15 eV at intermediate and large angles 10. The TCSs have been also measured in a transmission technique using a Ramsauer-type configuration in the 75-4000 eV energy range by Zeeca et al. (1992) 11. At the same time, Alle et al. reported absolute TCS and DCSs measurements for vibrationally elastic electron scattering from NH3 et al at incident energies 2-30 eV, using a crossed electron-molecular beam apparatus 12. While in a wider energy range 300-5000 eV, Garcia and Manero (1996) used a method based on a transmission-beam technique including a detailed error-source analysis 13. In another range of energy 400-4000 eV, Ariyasinghe et al. (2004) have measured the data from a linear transmission technique based on the electron-beam intensity attenuation through a gas 14. Recently, Jones et al. (2008) reported the data in the low energy range 20 meV-10 eV including both integral scattering and scattering into the backward hemisphere with high energy resolution 15. Furthermore, the elastic and inelastic scattering DCSs of high energy (35 keV) electrons scattered by NH3 molecules were measured separately for the first time by Lahmam-Bennani et al. 16-17 and Dugu et al. 18, using two independent experimental methods. Finally, let us notice that many discrepancies exist between the cross sections produced in different laboratories. As mentioned by Karwazs et al. the most serious deviations arise in the TCS maximum resonant region (up to 25%), around 10 eV, and at high energies (to 35%) 19.
On the theoretical side, Itikawa (1971) adopted a general form of electron-molecule interaction in the Born approximation and derived a cross section formula for the rotational transition in a symmetric-top molecule and applied it to the e-NH3 collisions to evaluate the DCSs for energies lesser than 0.1 eV 20. Many years later, Jain (1988) carried out calculation of the TCSs (elastic + inelastic) from 10 eV to 1000 eV, using a parameter-free spherical complex optical potential with different potential component models 21. As the author mentioned, the results were so distinct that their comparison with the experimental data can help to select the model describing well the scattering process. At the same time, Benarfa and Tronc (1988) investigated the vibrational excitation and then calculated the DCSs and integral cross sections (ICS) at low energies (3-10 eV); particularly they analyzed the angular distributions of the elastic peak of the nv1 series and of the v 4 vibrational mode 22. Furthermore, Pritchard et al. (1989) reported differential and momentum transfer cross sections of elastic scattering for e-NH3 collisions from 2.5 to 20 eV in the fixed-nuclei static-exchange approximation using the Schwinger variational principle 9. Sometime later, Gianturco (1991) developed a model - to calculate the DCSs and ICSs for electron-NH3 interactions - based on a free parameter correlation-polarization and exchange potentials, which play a fundamental role in describing the scattering of slow electrons from molecular targets23. In another calculation, Yuan and Zhang (1992) used the first-order Born approximation with the rotating molecule model, thus the total, differential, and momentum-transfer cross sections are reported for the vibrationally elastic scattering of electrons in the energy range 0.5-20 eV 24. Besides, Rescigno et al. (1992) developed an ab-initio optical potential study using Kohn variational model including the static-exchange and polarized-self consistent-field of low-energy 25. Their results demonstrate the sensitivity of the CSs to the short-range repulsion, long-range polarization, and the effects of the dipolar field particularly between 2 and 7.5 eV. Few years later, elastic and inelastic CSs for e-NH3 interactions are also calculated in the energy range 50-200 eV by Joshipura and Patel (1996) using a modified additivity rule by separating e-molecule interactions into short-range and long-range parts26. Furthermore, Liu et al. (1997) have used the semi-empirical formula, complex optical potential, and the additivity rule in the intermediate and high energy range to evaluate the TCSs from 10 eV to 1 keV 27. At the same time, Garcia and Manero (1997) used the empirical formula in the energy range 0.5-1 keV; their results reproduce sufficiently well (within 6%) their measurements for the series of investigated molecules (NH3, CH4, N2, CO and CO2) 28. The DCSs are also obtained from 8.5 to 30 eV by Lino (2005) using the Schwinger variational principle 29. As the Cartesian Gaussian functions basis - usually used in the method - is very effective only for short-range potentials, the authors introduced the plane waves as a trial basis set 29. Recently, Munjal and Baluja (2006) reported also the DCSs, ICSs, momentum transfer, and excitation cross sections for the low-energy (0.025-20 eV) electron-NH3 scattering, using the R-matrix method 30. Few years later, Limbachya et al. proposed two different methods to calculate the rotationally elastic CSs for electron scattering from NH3 attempting to demonstrate the possibility of producing robust cross sections over a wide energy range (0.01 eV to 2 keV) adaptable to any target 31. The UK molecular R-matrix code through the Quantemol-N software package is used to calculate elastic plus electronic excitation cross sections for incident energies below the ionization threshold of the target, while at higher energies the spherical complex optical potential formalism was used 31. Finally, note that the CSs for numerous polyatomic targets have been reviewed in these last decades by Shimamura 32, Hayashi 33, Morgan 34 and Karwazs et al. 19.
Despite the above-cited works, the differential and integral cross sections for electron elastic scattering by ammonia have not received all the attention merited. Regarding the works dedicated to the elastic scattering differential cross sections, they are very scarce in intermediate and higher energy range. Under these conditions, we propose in this paper to calculate elastic DCSs and ICSs for e-NH3 molecule interactions in the energy ranging from 10 eV up to 20 keV. Furthermore, the spherical complex optical potential including static potential and the fine effects like correlation-polarization and exchange potentials are considered and their effects discussed. The static potential is obtained here numerically from quantum calculation using molecular wave functions determined by Moccia 35 while the correlation-polarization and exchange potentials are rigorously selected from the literature. In the following sections, atomic units (a.u.) are used everywhere.
2.Theoretical model
The calculations of differential cross section
k is linked to the kinetic energy E by
2.1.Static potential
To evaluate the static potential, we use the ammonia molecular orbital functions determined by Moccia 35. In this description, each molecular orbital was expressed in terms of Slater-type functions all centered at a common origin (the heaviest atom). Thus, the ammonia target can be described by means of
where N
j
is the number of Slater functions used to construct the jth (with j varying from 1 to
and the angular part
For more details, we refer the reader to Refs. 35 and 37 where all the coefficients (
The electronic contribution is given for each molecular orbital j by
and the ionic one by
The symbols
2.2.Correlation-polarization potential
It is well established that NH3 is polar covalent moleculedue to the electronegativity difference between the nitrogen (higher) and the hydrogen atoms. Hence, e-NH3 interactions induce an additive potential due to the polarizability of the target induced by the incident electrical charge particularly at low velocities. The polarization potential
where
with
where E refers to the incident electron energy.
As proposed by Salvat et al. 42, we use here the polarization potential combined with the correlation one, called correlation-polarization potential. Different expressions of the correlation potential are found in the literature; the first expression chosen here is given by Padial and Norcross (1981) 43
and the second one is given by Carr and Maradudin (1964) 44
where
where
2.3.Exchange potential
In addition to the polarization phenomena of the target in the electron-molecule interactions, the incident electron can be captured by the target - particularly at low incident energies - and then the latter releases one of their bound electrons. This phenomenon known as electron exchange process needs another potential called exchange potential. Among the various formulas available in the literature, we have selected two expressions; the first one
where
The second exchange potential
where
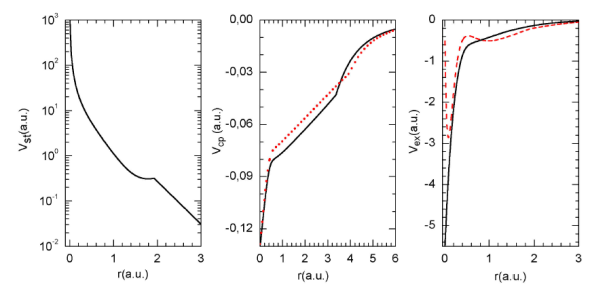
FIGURE 1 (Color online). Different potentials used in this work. (a) Static potentials used to describe the electron elastic scattering by ammonia molecules, (b) Correlation- polarization potentials V cp1 ( black solid line) and V cp2 (red dotted line), (c) Exchange potentials V ex1 (black solid line) and V ex2 (red dashed line).
Finally, note that here we have studied studied two expressions for the correlation-polarization potential (
3. Results and discussion
To evaluate the exchange potential (see Eq. (15)), we need, first, to calculate the electronic charge density, p(r), of the ammonia molecule. Figure 2 reports the obtained electronic charge density versus the radius r accordingly to Eq. (16), using the molecular wave functions determined by Moccia 35. The distribution exhibits two maxima located around 0.15 a.u. and 1.16 a.u, and one minimum around 0.5 a.u., as expected. The distribution shows no significant values over the radial distance r = 6 a.u. hence, the calculations can be achieved only in the range given by
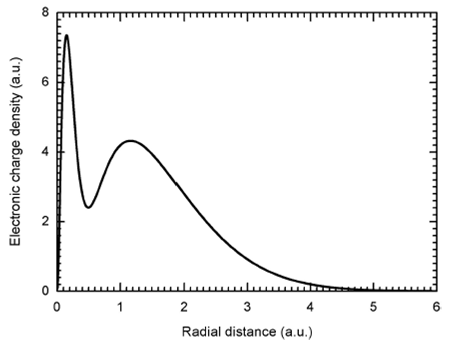
FIGURE 2 Electronic charge density of the ammonia molecule. The distance r refers to the center of the molecule, which is here merged with the heaviest atom center.
3.1.Differential cross sections
Differential cross sections for elastic scattering of electron by NH3 molecule are calculated for scattering angles varying from 0 to 360o and for numerous incident energies. First, these differential cross sections are reported in Fig. 3 (left panel) for 15 eV, 20 eV and 30 eV, where experimental data are available and only from 0 to 180o since they are symmetrical with respect to the axis
The DCSs obtained (left panel in Fig. 3) are important in the forward directions and lesser in the backward directions, while they are even smaller exhibiting a valley around the perpendicular directions, as expected. In general, the different exchange and correlation-polarization potentials, investigated here, provide quasi-identical DCSs and a good agreement is observed throughout the angle range for all the energies investigated. However, at lower scattering angles, the calculated DCSs exhibit little discrepancies particularly at lower energies. In fact, these discrepancies related to the form of the correlation-polarization potential considered are directly linked to the polar nature of the target since there is a mutual influence between the electric dipole of the molecule and the charge of the projectile. It is then evident that this influence, responsible of the discrepancies, became relatively important at lower incident energies, since the projectile spends a relatively important time near the target molecule. In addition, the DCS curves show the existence of a profound minimum, in the exhibited valley, whose depth depends on the form of the tested correlation-polarization and exchange potentials. The minima are located around
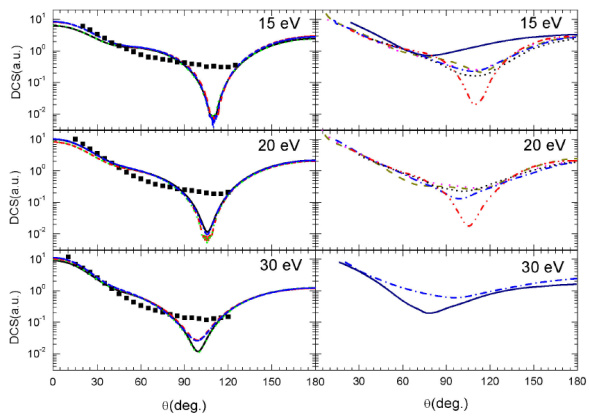
FIGURE 3 (Color online) In left panel: Comparison between calculated DCSs for electron elastic scattering by ammonia molecule at 15, 20, and 30 eV for various potentials: V st (r) + V cp1 (r) + V ex1 (r) (solid black line), V st (r) + V cp1 (r) + V ex2 (r) (dashed red line), V st (r) + V cp2 (r) + V ex1 (r) (dotted green line) and V st (r) + V cp2 (r) + V ex2 (r) (blue dash-dotted line). Experimental data are taken from 12 (black solid squares) and 10 (red open circles). In the right panel: theoretical results are taken from 9 (short-dashed black line), 23 (dash-dotted blue line), (24) (dash-dotted-dotted red line), 25 (dotted magenta line), 29 (solid navy line), and 30 (dashed dark-yellow line).
In Fig. 4, we report the DCSs for electron elastic scattering at intermediate incident energies (300 eV, 400 eV, 500 eV, and 1 keV) for the four combinations of correlation-polarization and exchange potentials investigated in this work. These latter provide quasi-identical curves, and an overall agreement is observed in the whole angle range for all the energies investigated. The effects of the fine contributions (correlation-polarization and exchange potentials) no longer appear even in the range of lower scattering angles. Besides, the observed minima at low incident energies disappeared from the value of 200 eV (not reported here). In addition, we have reported in Fig. 4 the experimental data provided by Harsbarger et al. 5 (black solid squares) and by Bromberg 6 (red open circles) for the scattering angles from 2 to 10o. Our calculated DCSs appear slightly lesser than the experimental ones around 2o and seem to be in good agreement beyond this scattering angle value. Finally note that, to the best of our knowledge, there are no other results neither experimental nor theoretical in larger angle range to compare with.
3.2.Integral cross sections
Integral cross sections for electron elastic scattering from NH3 molecules are also calculated using the four above-cited combinations including the static, correlation-polarization, and exchange potentials. The energy distribution for elastic scattering is obtained by integrating numerically the differential cross sections overall the scattering solid angle
The various obtained results are presented in Fig. 5a for the incident energies ranging from 10 eV to 20 keV, and for the four potential combinations investigated. As expected, the amplitude is important at lower incident energies and decreases monotonically with the increasing of the impact energy. In addition, the four calculated ICSs exhibit a good agreement at intermediate and high incident energies. In fact, the little discrepancies observed at low energies (
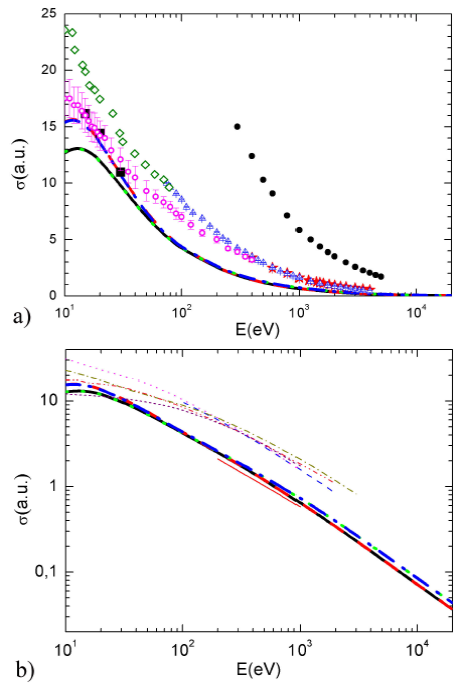
FIGURE 5 a) (Color online) Comparison between calculated ICSs for electron elastic scattering by ammonia for various potential combinations: V st (r) + V cp1 (r) + V ex1 (r) (solid black line), V st (r)+V cp1 (r)+V ex2 (r) (dashed red line), V st (r)+V cp2 (r)+ V ex1 (r) (dotted green line) and V st (r)+V cp2 (r)+V ex2 (r) (dashand-dotted blue line). Experimental data are taken from 12 (black solid squares), 7 (magenta open circles), 11 (blue up triangles), 14 (red stars), 13 (solid black circles), and 8 (olive diamonds). b) (Color online) As in Fig. 5a. Thin lines are theoretical results taken from 21 (red solid line and dark-yellow dashed dotted line), 26 (dashed blue line), 27 (dotted magenta line and short dashed purple line) and 31 (dashed-dotted-dotted pink line).
The obtained cross sections (thick lines) using different potentials are also reported in Fig. 5b where they are compared to the theoretical results existing in the literature (thin lines) taken from 21 (solid red line and dashed dotted dark-yellow line), 26 (dashed blue line), 27 (dotted magenta line and short dashed purple line), and 31 (dashed dotted-dotted pink line). Note that the shapes of all the different cross sections (thin lines) are identical with that calculated in this work (thick lines). However, the magnitudes of our CSs are, in general, lesser than the former except that of Jain 21 (solid red line). In fact all the different previous CSs include the inelastic contribution except that of Jain 21 where the elastic CSs are considered in the static-exchange-polarization (SPE) model. Finally, it is worth noting that the CSs reported by Jain 21 including the absorption part (dashed-dotted dark yellow line) are higher in magnitude than that obtained in this work confirming in this way these arguments.
4. Conclusion
In the present work the interactions of electron with ammonia molecule are investigated and the differential and integral cross sections are calculated for the elastic scattering in the partial wave formalism. The target molecular state has been described by means of a single-center molecular wave function, while the interactions by means of complex optical potentials including a static contribution - numerically obtained, here, from quantum calculations - and fine effects like correlation, polarization and exchange phenomena rigorously selected from the literature.
The obtained DCSs for different potentials investigated show clearly the role played by the correlation, polarization and exchange phenomena particularly at lower scattering angles and lower incident energies. The calculated DCSs have shown good agreement with the experimental data both in shape and magnitude, demonstrating in this way the power of the developed model, particularly at intermediate and higher energies.
In addition, the integral cross sections calculated from 10 eV to 20 keV for different combinations of potentials investigated here show clearly a good agreement except at lower energies (











 nueva página del texto (beta)
nueva página del texto (beta)



