Theoretical investigation EuTiO3 in three structures; optical, electrical and magnetic properties

Zaari, H.; Azahaf, C.; Lakouari, N.; Benyoussef, A.; EZ-Zahraouy, H.; El Kenz, A.; Zaari, H.; Azahaf, C.; Lakouari, N.; Benyoussef, A.; EZ-Zahraouy, H.; El Kenz, A.

doi:10.31349/revmexfis.64.553

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista mexicana de física

versión impresa ISSN 0035-001X

Rev. mex. fis. vol.64 no.6 México nov./dic. 2018 Epub 05-Nov-2019

https://doi.org/10.31349/revmexfis.64.553

Research

Theoretical investigation EuTiO₃ in three structures; optical, electrical and magnetic properties

H. Zaari^a^*

C. Azahaf^a^⋅

N. Lakouari^a^b^†

A. Benyoussef^a^‡

H. EZ-Zahraouy^a^⋆

A. El Kenz^a^⊛

^{^a} Laboratoire de Matière Condensée et Sciences, Interdisciplinaries, P. O. Box 1014, Faculty of Sciences, Mohammed V University of Rabat, Morocco.

^{^b} Facultad de Ciencias Químicas e Ingeniería, Universidad Autónoma Del Estado de Morelos, Av. Universidad 1001, Col. Chamilpa, 62209, Cuernavaca, Morelos, Mexico.

Abstract

We present a systematic first-principles study of the structural, magnetic and optical properties of perovskite-structure EuTiO₃. This compound exists in different structures: cubic, tetragonal and presents multiferroic properties. Comparing the formation energy between tetragonal and cubic structures, the system has a tendency to symmetry lowering structural deformations composed of rotations of the oxygen octahedra, especially the I₄/mcm phase is the most stable structure. Our calculations of the high symmetry cubic structural prototype show an antiferromagnetic order type G. We discuss the dynamical stability of Pm-3m, P4mm and I₄-mcm structures, and the influence of some parameters on the magnetic coupling and the electrical polarization.

Keywords: Multiferroic order; magnetic coupling; polarization; Wien2K

PACS: 71.20.-b; 75.25.-j; 71.15.Mb

1. Introduction

The coexistence of electrical and magnetic order in magnetoelectric multiferroics compounds has attracted many researchers to understand this behavior, and to have new development of novel approaches for obtaining functional responses, either linear magnetoelectric effect or crossed switching phenomena at room temperature ^[1]. The main goal is to control polarization with a magnetic field or magnetism by an electric one, such as electrically tunable microwave components and spintronic devices ^[2], and the long-searched electrical-writing, magnetic-reading random access memory ^[3].

The multiferroic system could be a superlattice, 3D compound or thin film 2D, the research is focused with the novel approaches to obtain single-phase materials with room temperature magnetoelectricity a highly topical set of materials like those ABO3 perovskite oxides, in which multiferroicity is chemically engineered by placing ferroelectrically and magnetically active cations in A- and B-site, respectively. This is the case of the BiFeO3 and BiMnO3 perovskites ^[4]. Other type of perovskite has rare earth element in A sites, and transition metal in B sites, like EuTiO3, TbMnO3.

Europium Titanate, EuTiO3, was the first ternary compound of divalent Eu2+ to be identified. It is a G-type antiferromagnetic (AFM) with lower magnetic ordering temperature of 5.3 K, consistent with the highly localized 4f electrons on the Eu2+ ions. ^[5]. Until recently, its structural ground state was thought to be the ideal cubic perovskite structure, with Pm-3m symmetry ^[6].

EuTiO3 is insulator with a high dielectric constant at low temperature, indicating quantum paraelectric behavior and proximity to ferroelectric instability ^[7]. Strong interactions between the magnetic and dielectric properties have been reported ^[8-^10]. EuTiO3 has been considered as the prototype for studying quantum paraelectric behavior in magnetic systems.

Experimental and theoretical works have been done in^[11] and both of them show strong M- and R- point in Brillouin zone instabilities in cubic Pm-3m structure. The system has a tendency to have another structure stability with antiferrodistortive rotations of the octahedra. The system has a lower energy in one of these structures: I4/mcm, Imma, R-3c.

In EuTiO3, the antiferrodistortive transition occurs near 282 K. as discussed in ^[12]. Several phenomena could be discussed in this compound due to the large magnetic moments, and motion of the oxygen octahedra around the Eu and Ti ions like magneto-electric coupling, phonon-spin coupling, etc. especially the unusual mode of coupling between magnetism and the tetragonal soft mode, as discussed by Scot^[12].

Other works have been focusing on the phase diagram of a quantum paraelectric antiferromagnet EuTiO3 under an external electric field using Landau-Ginzburg-Devonshire theory. It was shown that the application of an external electric field leads to the appearance of a ferromagnetic phase due to the magnetoelectric coupling. In particular, at some electric field larger than the critical field (Ecr), which equal to Ecr=0.40×106 V/cm the FM phase appears. The results show the possibility to control multiferroicity, including the FM and AFM phases, using an electric field application ^[13].

Magnetoelectric coupling in EuTiO3 is exceptionally high due to the strong contribution of magnetic Eu cation in low energy polar mode, and large coupling of the spins to the optical phonon modes involved the incipient ferroelectric transition which has been computed in ^[14] and has value of 9 cm^-1. In contrast to other multiferroics which have non-magnetic ions like Bi in BiFeO₃ or Y in YMnO₃, in the last system, the magnetoelectric coupling is usually smaller.

The ferroelectric phase with magnetic ordering can be forced by using heterostructure or using mismatch strain on the thin film by substrate like EuTiO₃ grown on DyScO3 substrates ^[15].

Microscopic origin of the mixing characteristics of the low-energy polar mode in cubic EuTiO₃ is the coupling of the 4f orbitals of Eu2+ with the 3d states of nonmagnetic Ti⁴⁺^[16] the later has an effect on the mixing character on the low-energy polar mode and an instability of EuTiO₃. This effect was recently studied by Birol and Fennie ^[17]. It was found that partial occupation of the d-states on Ti due to hybridization drives EuTiO3 away from ferroelectric instability.

This conclusion is compatible with the results of Ref.^[18], where it was shown that the increasing volume of cubic EuTiO₃, i.e. decreasing f-d hybridization, turns the low-energy mode to be unstable, with Slater-type atomic displacement. Nevertheless, it is still not clear what is the effect of the oxygen vacancy on the structural stability of EuTiO₃.

According to these all results cited above, our study will be focused on the electronic, magnetic and optical properties of EuTiO₃ in cubic, pseudo-cubic, and tetragonal structures, using the first principle methods, we will confirm the instability of cubic structure and magnetic order change in the different structure. The electric polarization is also computed, the effect of oxygen vacancy will also be studied.

2. Theoretical investigation

2.1. Computational details

In order to describe more the electronic, magnetic and optical properties, for our system, all the calculations are performed using the FP-LAPW method, as implemented in the WIEN2k code ^[19], Generalized Gradient approximation (Perdew-Burke-Ernzerhof form) ^[20] is used to treat the exchange correlation functional. The relativistic and spin-orbit effects are also taken into account. The basis quality is measured by the product Rmin×Kmax where Rmin is a minimal atomic sphere radius and Kmax is a length of maximal reciprocal lattice vector). We take Rmin×Kmax=7 following the Monkhorst?Pack scheme ^[21], self-consistency is obtained using 7×7×7 k-point meshes for the first Brillouin zone integration (IBZ). All these values have been chosen so as to ensure the total energy and charge converged to better than 10-5 Ry and 10-3 respectively.

The cut-off energy, which defines the separation between the core and valence states, was set to -6.0 Ry, the tetrahedron method is used for the calculation of the total energies, electronic structure, and magnetic properties.

The polarization values given in our work are computed using the Berrypi package ^[22].

3. Ab initio results

3.1. Optimizations

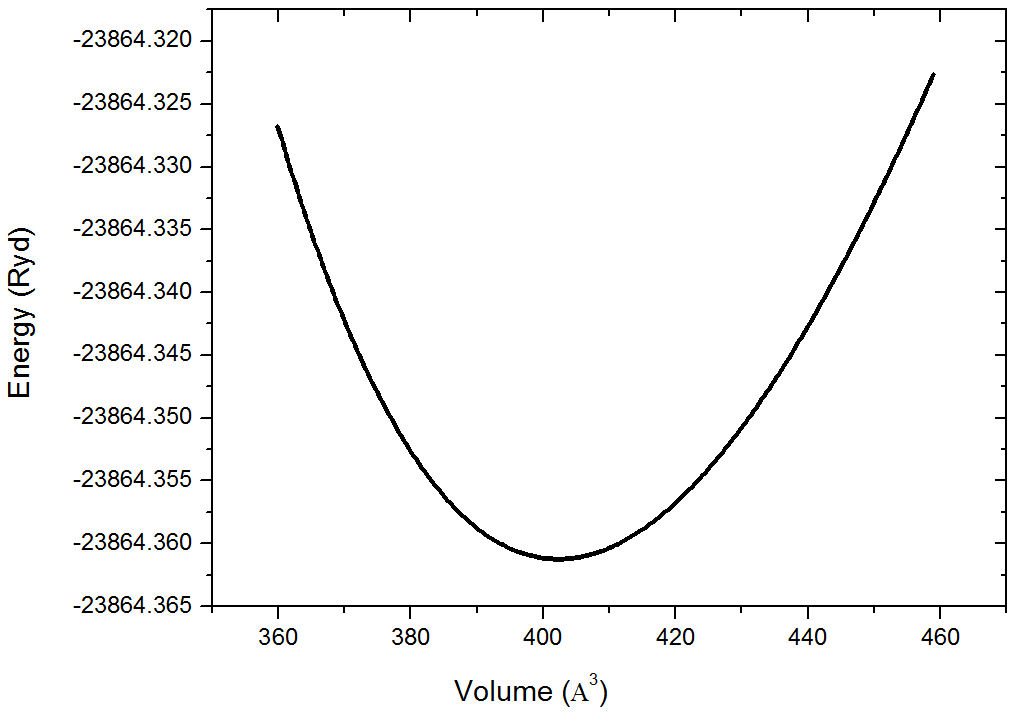
In order to investigate the electronic properties of a cubic system, we start our calculations by the volume optimization as it displayed in Fig. 1.

Figure 1 Volume optimization of EuTiO₃ in cubic structure.

EuTiO3 has a cubic structure (space group Pm3-m) with a lattice parameter of 3.905 Å at room temperature ^[23]. The optimization gives a value: a=3.906 Å which is very close to the experimental one.

EuTiO3 has a cubic structure at room temperature, at low T, it exhibits tetragonal structure; but also, pseudo cubic (P4mm), the tetragonal phase can be considered as supercell of 2a×2a×2c× with a=c is the lattice parameter of the cubic structure.

The tetragonal structure has a lower formation energy, as we can see the values in Table I. The cubic and pseudo-cubic phases are instable; therefore, we expect ferroelectric behavior in both of them, the same remark we have in the case of oxygen vacancy.

Table I. Lattice parameter and formation energy for EuTiO3 in different phase, the values of lattice parameter are taken from ^[24,^25].

	Pm-3m(221)	P4mm (99)	I4/mcm (140)	Cubic phase with
	Cubic 300 K	Pseudocub 93 K	Tetragonal (100 K)	O-vancacy-8.3%
Lattice parameters Å	a=3.06	a=3.902	a=5.51	a=3.306
		c=3.908	c=7.8
Formation energy	-2.06 ryd	-2.04	-3.21	-0.69 rydb

3.2. Electronic properties of Cubic and tetragonal structure

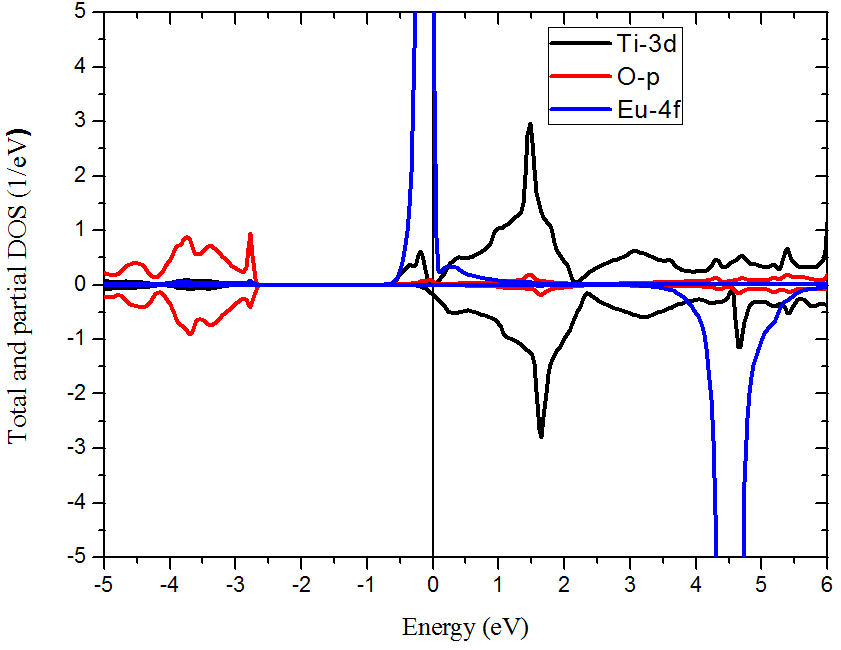
The total and partial density of states (Fig. 1 and 2) show the only magnetic atom is Eu having Eu²⁺ and 4f⁷ in valence states, the 4f states are localized near to Fermi level given a metallic character in the system. With a magnetic moment of 6.9 μb. The small band of Ti-3d states and p states of Oxygen at Fermi level indicating p-d hybridization.

Figure 2 The total density of states for cubic structure.

In tetragonal structure I4-mcm (Fig. 3) the system became an insulator having a band gap of Eg=0.28 eV. The principal 4f states of Eu still remain near the Fermi level, and p-d states of O and Ti also. To explain this change of behavior we have plotted the crystal field of 3d-Ti, the results as displayed in Fig. 4, show the 3d states are splited in e2g and t2g level under crystal field. Below Fermi level the states situated there are originated from O- p states and Ti-3d states specially -DX2-Y2, thus we have a deformation in crystal field as known to John Teller effect. This effect allows the system to have a small band gap.

Figure 3 The partial density of states shown (3d states, p and f states) for cubic structure.

Figure 4 Total density of states in tetragonal phase (I4-mcm).

3.3. Magnetic properties of cubic and pseudo, cubic and tetragonal phase

In order to determine the stable ground state of EuTiO₃, the total energy calculations corresponding to ferromagnetic (FM) and antiferromagnetic (AFM) phases must be performed. Therefore, we consider 2a×2a×c supercell for three possible different configurations: Ferromagnetic (FM), antiferromagnetic type A and antiferromagnetic type G, all these configurations are displayed in Fig. 5. The results are presented in Table II.

Table II. Magnetic coupling and stability in different case studied for EuTiO₃.

	Magnetic coupling (eV)	stability
a=3.906	J1=-0.3	AFM G
	J2=-0.44	AFM A
3.92	0.083	FM
Structure P4mm	0.041	FM
I4 mcm	J=-0.4	AFM G
Displacement of O atoms	J=0.069	FM

Figure 5 Partial density of states in tetragonal phase (I4mcm). (3d states of Ti and p-O).

The ferromagnetic behavior is very sensitive to volume system or type of atomic positions. With an optimized value of lattice parameter, we have an antiferromagnetic phase G-type in cubic and tetragonal structure, while the small increase of lattice parameter value allows the system to get a weak ferromagnetic coupling.

The other cases presented in Table II have ferromagnetic behavior, we can give the following explanations for this change:

-According to the rule of Good-enough Kanamori, the angle between the atoms plays an important role ^[26] in magnetic behavior, when the angle between Ti and Oxygen atoms equal to 180∘, then we get an antiferromagnetic phase.

-In Table II, for the last case, the displaced oxygen position of 0.01 in the z-direction, and third case, the angle of O-Ti-O is no more plane as displayed in Fig. 6, we noticed this angle by A which equal to 162∘, then we have ferromagnetic behavior. The oxygen atom plays an important role as mediator to conserve this behavior.

Figure 6 Schematic representation of three possible magnetic configuration. Only the Eu atoms are displayed.

3.4. Optical properties and the parameters which act on the polarization

In order to complete our study, the ferroelectric system has a high value of dielectric constant, so we have computed the optical properties of cubic and tetragonal phase (I4-mcm) to prove our results about the polarization change between both structures.

The dielectric constant value decreased from ε(0)=22 in cubic structure to ε(0)=18 in the tetragonal phase, (Fig. 7 and 8) thus the system is no more ferroelectric as confirmed by weak value in polarization (Table IV). The main edge situated near to zero energy indicates the electronic transition from Eu-4f states to Ti-3d states.

Figure 7 Pseudo-cubic structure of EuTiO₃.

Figure 8 Dielectric function of EuTiO₃ in cubic phase.

Table III. Value of polarization in both ferromagnetic and AFM cases for cubic structure.

Cubic	FM	AFMG	Ti-O band-
structure	(C/m²)	(C/m²)	lengths (Å)
a=3.906 (Å)	P= 0.51	0.524	1.95
a=3.92(Å)	0.78	0.89	1.96
Displacement z=+0.01	P=0.54	0.58	1.92

Table IV. Value of polarization in different cases of EuTiO₃.

	Polarization C/m²
Cubic structure	0.6
Experimental value	∼0.1-0.5 [27]
O vacancy	0.29
Tetragonal structure I4-mcm	0.35
P4 pseudo cub (P4mm)	0.76

This material contains magnetic Eu with spin 7/2, which undergoes antiferromagnetic order at TN ∼ 5.3 K ^[5]. Magnetic order in this material couples to polarization fluctuations as shown in Table III. Electric polarization in this material is due to the variations of Ti-O bond-lengths from their equilibrium values.

The polarization value computed is very close to the experimental one in a cubic structure, we noted a high dependence between polarization, magnetic order and structural properties like defect on strain (change in lattice parameter). These results confirm the ferrodisplacive character of this material.

Figure 9 Dielectric function of EuTiO₃ in tetragonal phase.

To explain these results many physical notions could be used here, because our system present magnetic and ferroelectric properties, and instability in lattice related to the phonons vibration.

The so-called “soft mode” theory is a theoretical ferroelectric phase transition model in which a mode of vibration of the crystal lattice (or phonon) plays a predominant role. The most commonly studied and exposed case is that of a phase transition as a function of temperature T, we can identify this transition by considering the change of polarization versus T or dielectric function versus T.

The static dielectric value is related to the optical and acoustic polar phonon mode, as follows ^[26]:

ε0=ε∞∏ilω2LOiω2TOi (1)

According to this relation, the change of dielectric constant is related to the polar phonon mode, which originates from the rotation motion of TiO₆ octahedra and the change of angle between Ti and O.

All these parameters affect the polarization and ferroelectric behavior which is directly related to the spin order and a super exchange between Eu²⁺ 4f spins via the 3d states of the Ti⁴⁺ ions.

4. Conclusion

Finally, in this work, we have tried to describe more the magnetic, optical properties of three structures of EuTiO₃ which exist in three different temperatures, EuTiO₃ is antiferromagnetic G-type and has a strong value of dielectric constant and electric polarization. We have shown that the magnetic coupling is very sensitive to the volume change,and the angle between Ti and O.

In this system, known as multiferroic, a structural transition is accompanied by the change in magnetic or electric order, strong magneto-electric could be proved and more detailed, these results open the door to higher temperature implementations of ferromagnetic or ferroelectric ordering for an important application such as: magnetic sensors, high-density multistate memory elements, wireless powering of miniature systems.

Acknowledgments

We thank P. Blaha and K. Schwarz for the Wien2K code and the wien2k users for very useful discussions.

References

1. J. F. Scott, J. Mater. Chem. 22 (2012) 4567. [ Links ]

2. Fusil, V. Garcia, A. Barthelemy and M. Bibes, Annu. Rev. Mater. Res. 44 (2014) 91. [ Links ]

3. C.M. Fernandez-Posada, H. Amorin, C. Correas, O. Pena, M. Alguero, and A. Castro, J. Mater. Chem. C. 3 (2015) 2255. [ Links ]

4. T. R. McGuire, M. W. Shafer, R. J. Joenk, H. A. Alperin, and S. J. Pickart, Journal of Applied Physics 37 (1966) 981. [ Links ]

5. G. McCarthy, W. White, and R. Roy, Journal of Inorganic and Nuclear Chemistry 31 (1969) 329. [ Links ]

6. T. Katsufuji and H. Takagi, Phys. Rev. B 64 (2001) 054415. [ Links ]

7. Q. Jiang and H. Wu, Journal of Applied Physics 93 (2003) 2121. [ Links ]

8. H. Wu and W. Shen, Solid State Communications 133 (2005) 487. [ Links ]

9. H. Wu , Q. Jiang , andW. Shen , Physics Letters A 330 (2004) 358. [ Links ]

10. D. Bessas et al., Phys. Rev. B 88 (2013) 144308. [ Links ]

11. J.F. Scott, npj Computational Materials 1 (2015) 15006. [ Links ]

12. M.D. Glinchuk et al., Phys. Rev. B 89 (2014) 014112. [ Links ]

13. T. M. Holden, et al., J. Phys. C Solid State Phys. 4 2127-2138 (1971). [ Links ]

14. H. Akamatsu et al., Phys. Rev. B 83 (2011) 214421. [ Links ]

15. T. Birol and C. J. Fennie, Phys. Rev. B 88 (2013) 094103. [ Links ]

16. K. Z. Rushchanskii, N. A. Spaldin, and M. Lezaic, Phys. Rev. B 85 (2012) 104109. [ Links ]

17. M. Allieta et al., Phys. Rev. B 85 (2012) 184107. [ Links ]

18. K. Schwarz, P. Blaha, G.K.H. Madsen, Comput. Phys. Commun. 147 (2002) 71. [ Links ]

19. J.P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 77 (1996) 3865. [ Links ]

20. J. Monkhorst, J. Pack Phys. Rev. B 13 (1976) 5188. [ Links ]

21. S. J. Ahmed, J. Kivinen, B. Zaporzan, L. Curiel, S. Pichardo and O. Rubel, Comp. Phys. Commun. 184 (2013) 647. [ Links ]

22. B. Ravel and E. A. Stern, Physica B 209 (1995) 316. [ Links ]

23. M. A. Carpenter and C. J. Howard, Acta Cryst B 65 (2009) 134. [ Links ]

24. K. Z. Rushchanskii , N. A. Spaldin , and M. Le/ zˇaić, Phys. Rev. B 85 (2012) 104109. [ Links ]

25. J. Töpfer and J. B. Goodenough, J. Solid State Chem. 130 (1997)117. [ Links ]

26. B. J. Kennedy et al., Journal of Physics: Condensed Matter 26 (2014) 495901. [ Links ]

Received: July 06, 2018; Accepted: July 11, 2018

^* e-mail: halimazaari@gmail.com;

^⋅ chaimae.azahaf@gmail.com;

^† yn.lakouari@gmail.com;

^‡ zbenyous.a@gmail.com;

^⋆ ezahamid@fsr.ac.ma;

^⊛ elkenz@fsr.ac.ma

This is an open-access article distributed under the terms of the Creative Commons Attribution License