1. Introduction
Therapies like electrochemical treatment (EChT) [1], electrochemotherapy (ECT) [2] and radiofrequency ablation (RF) [3] have emerged as safe and effective treatments for solid tumors with minimum damage to the organism. During application of these therapies, tissue heating arises due to conduction losses (i.e., resistive heating from ion movement) [4]. Thermal spread in biological tissue may be measured using an infrared thermograph device [5]. Images of surface temperature and false-positive and false-negative constitute limitations of the infrared thermography method [6,7]. Therefore, several researchers have addressed their efforts to know how the temperature is distributed in a tissue (i.e., the tumor) [8-10]. Furthermore, mathematical modeling is used [8,11-13]. These studies evidence that thermal modeling is more complex than electrical ones because diffusion process depends on time. Heat transfer has an important role in biological systems of living beings [11,14,15]. The Pennes bioheat equation is crucial for the majority of the bioheat transfer simulations [16]. It has been used when the internal heat generation of tissue is produced by its metabolism [17]. Additionally, Pennes bioheat equation permits to describe the energy conservation equation for biological heat transfer on the basis of the classical Fourier’s law of heat conduction [5]. Analytic modeling of temperature distribution is based on solving the linear bioheat transfer equation for tissue, which is the general heat equation for conduction, with added terms for heat sources [8-10,18].
Pennes bioheat equation has been previously used to model temperature distribution in non-homogenous tissues [11,19,20], in which heat sources (one or several electrodes) are inserted. Gupta et al. [21] make a numerical study on heat transfer in tissues for different coordinate systems and under different boundary conditions (first kind, second kind and third kind). They conclude that during thermal therapy, probe shape, boundary conditions and internal heat source should not be the same and must be changed from one organ to the other in the human body.
Kumar et al. [22] report that treatment of cancerous cell is independent of the generalized coordinate system considered at the thermal ablation position. Additionally, Pennes bioheat equation has been used to describe the heat transfer for targeted brain hypothermia, which is a result of the decreasing arterial blood temperature [23].
We are not aware on applications of the bioheat equation for two media (tumor and the surrounding healthy tissue) with different biological, electrical (electrical conductivity and electrical permittivity), mechanical and thermal properties, as reported in [24,25]. Besides, the thermal treatment of several tumor nodules in tissue/organism simultaneously has not been reported in the literature.
In this study, a modification of the linear bioheat equation is proposed to calculate the temperature in a multi-centric tumor and the surrounding healthy tissue, considering them as linear, heterogeneous and anisotropic media of arbitrary shapes. Besides, in this generalized equation the thermal, electrical, mechanical and biological properties of each biological tissue are considered.
2. Theory
2.1 Model assumptions
Heat transfer among the tumors occupying the regions
where
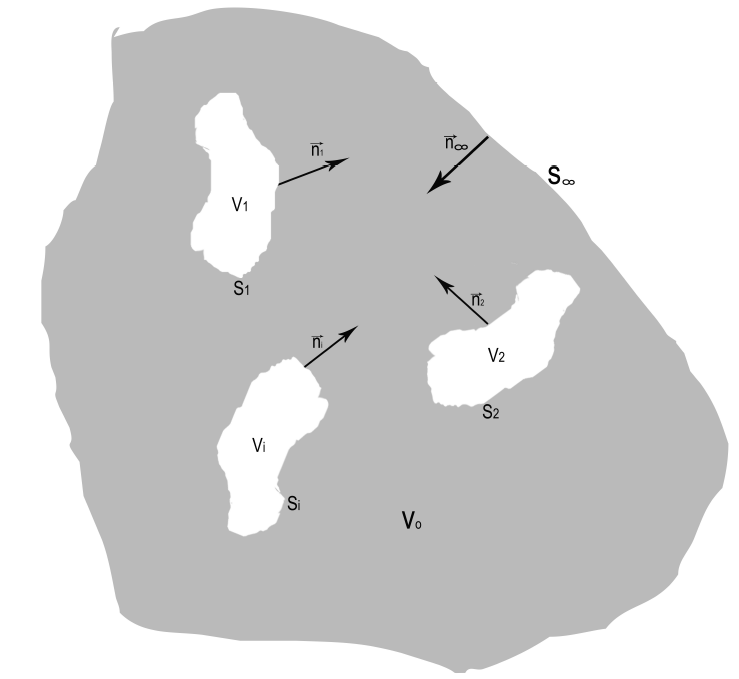
FIGURE 1 Schematic representation of work region: V0 is
the region that occupy the surrounding healthy tissue and contain
several tumors of different sizes
Vi(i = 1; : : :
;N), where Vi is the -th tumor volume
and N is the amount of tumors. Parameters
Si (i = 1;
2; : : : ;N) and S1 represent
surface boundaries and surface very far from the tumors,
respectively. Besides,
Although the heat sources are in the tumors, Joule heating terms are different on
each tissue. The parameter
The electric potential
The Joule heat is calculated by means of
In this study, Eq. (1) is addressed
to EChT, although it can be indistinctly used for EChT, ECT or RF. In this case,
Let us denote the initial distribution of
It is important to assess
Matching boundary conditions on the surfaces
where
Finally, the temperature distribution at points away from the tumors satisfies the following condition
Considering the above-mentioned assumptions and the change of variables
With
To deal with
Note that Eq. (4) is not altered and Eq. (5) adopts the form
2.2 Green Functions
As Eq. (4) (matching boundary
conditions) and Eq. (6) are not
homogeneous, let us introduce the Green functions of the problem for the tumors
and the surrounding healthy tissue
The independent term
Usually, the Green function is employed in the solution method of the Dirichlet boundary problem and Neumann boundary problem (normal derivative specified on the boundary). In the present model, Dirichlet and Neumann conditions are substituted by matching boundary conditions. So, the usual approach must be changed: the initial condition and matching boundary condition for Eq. (11) are
2 for
The condition at infinity is not changed:
If
and the same boundary conditions for
we can proceed in the following way: multiplying Eq. (6) by
Considering the vector identity (see Eq. (9) in [29])
with
because
Applying the divergence theorem to Eq. (19), we deduce that
where
The integral extended to
The minus sign in the integrals is explained because Maxwell normal is opposite to that of Gauss.
Integrating Eq. (17) and using Eqs. (20) and (21) yields
where
Note that, according to the definition of
Therefore, initial condition (12) implies that
Two direct consequences follow from Eq. (22): the reciprocity principle
and the formula
The reciprocity principle (25)
means that the influence in
The Eq. (26) evidences that
The proof of Eq. (25) is completed
by taking
and Eq. (25) follows, which is clear from Eq. (22).
Equation (26) follows using Eq. (24), Eq. (25), the fundamental property
of delta function and substituting,
The second term of Eq. (26) is zero because of Eq. (9). As a result, Eq. (26) can be rewritten as
for every
We set
The desired solution
2.3 Calculation of the Green functions by means of eigenfunctions
From Eq. (27), the required
solution is given in terms of the complementary conditions of the formulated
problem, if Green functions are known. An usual method to calculate these
functions consists in expanding them in terms of eigenfunctions of the operator
Assuming the following boundary conditions:
the domain of
such that
The analysis relative to Eq. (21)
shows that the domains of the operator
Besides,
The scalar product arises from integration of Eq. (32). This brings about that the second term in the right hand side of Eq. (32) be zero, by an analogous calculation to Eq. (21), resulting that
because the tensor is also positive. Hence, the eigenvalues (
Note that the eigenfunctions of
From Eq. (31), it follows also
that there is an orthonormal and complete system (
This permits the calculation of the Green function, given by
Substituting Eq. (36) in Eq. (11) and using the definition of eigenfunction, yields
From Eq. (36) and Eq. (37) results
Suppose
to obtain an ordinary differential equation
The solution of Eq. (40) is given by
where
Substituting Eq. (41) into Eq. (39) and using the mentioned result in Eq. (36), we obtain the expression of the desired Green function, given by
From Eq. (43), Green functions are
zero for
Note that the structure of Eq. (43) shows that anisotropy and inhomogeneity of media appear only in eigenfunctions.
Substituting Eq. (43) into Eq. (26), one obtains
3. Remarks on generalized Pennes equation
The formal solution (44) is compact
and obtained under quite general suppositions (linearity and
It is interesting to note that the solution (44) allows us to know the temperature distribution in the tumor volume and in its surface separately. Increase/decrease of the temperature gradient between the tumor volume and its surface could be induced. This can be possible by controlling the temperature generated by any geometry of electrode array reported in the literature [13,33-37] and the blood perfusion in the tumor. These aspects agree with the ideas of Ma et al. [23].
On the other hand, the solution (44)
is valid for electrodes of any shape [36].
Furthermore, this mathematical formalism permits to suggest strategies to treat each
nodule individually, depending on its stiffness, histogenic characteristics, shape
and electrical properties. The dielectric properties of biological tissues have been
published by several researchers [4,38]. Nevertheless,
The spatial distributions of the temperature, electric field strength and electric current density may be calculated in a realistic tumor model using finite element methods, taking into account the work of Korshoej et al. [40]. Nevertheless, it is suggested for EChT the integrated analysis of the electric potential, temperature, electric field strength, electric current density, pH and tissue damage spatial distributions generated by any geometry of electrode in the tumor and its surrounding healthy tissue, as reported in [13,37]. It is important to note that the antitumor mechanism more accepted in EChT is the induction of toxic products from electrochemical reactions [27,28,36].
In addition to the above mentioned, the solution (44) can be implemented in a numerical algorithm for the simulations. A further study can be carried out to simulate all physical quantities above mentioned and tissue damage in realistic anisotropic media with arbitrary shapes, electrode arrays with different geometry and arbitrary shape of the electrode. As the solution (44) is obtained for constant initial condition, it would be interesting to know how the solution (44) changes when spatially dependent initial condition is used, as reported in [5].
4. Conclusions
In conclusion, a general method is developed to calculate temperature distributions in two coupled linear and anisotropic media (solid tumor and the surrounding healthy tissue). This approach can be easily generalized to multi-centric tumors in a tissue or to several tumors (primary or metastasis) in the organism by changing the summation indices. For this propose, the method of Green functions is extended to include matching boundary conditions.











 nueva página del texto (beta)
nueva página del texto (beta)


