1. Introduction
Spintronics is the investigation of the fundamental spin of the electron and its combined magnetic moment, adding to its essential electronic charge, in solid-state devices [1]. Furthermore, to charge state, electron spins are used as a further degree of freedom, with employment in the performance of data storage and transfer. Spintronic devices are almost frequently synthesized in dilute magnetic semiconductors (DMS), Perovskite, and Heusler alloys and are of exceptional attraction in the field of quantum computing and neuromorphic computing [2]. Spintronics is a field of study in which, researchers are looking for materials to ameliorate the accomplishment of their electronic and magnetic properties and get a large half-ferromagnetic (HM) gap (G HM ). The HM i.e., spin-flip excitation, gap is identified to be the least possible energy with respect to the Fermi level of the majority (minority) spin between the minimal energy of the conduction bands and the absolute value of maximum energy of the valence bands [3,4]. Last decade, several experimental and theoretical research have been developed for this purpose. Recently, multiple works have treated the magnetic properties of the binary semiconductor III-V and II-VI doped by transition elements, Mn-doped InSb [5], Cr doped InSb [6], V doped GaP [7], Co-doped ZnS and (Al, Co) co-doped [8], and Mn-doped ZnO [9]. Shabir et al. studied the double perovskites system Ba2CoUO6 and report half-metallic comportment, with a half-metallic gap G HM = 1.98 eV [10]. A. Rafi et al. studied the perovskite selenide and tellurite compounds CoSeO3, CoTeO3, NiSeO3, and NiTeO3 [11]. The half-Heusler Alloy MgCaB has been investigated by A. Abada [12], with a value of G HM of about 0.305 eV.
This aim of this work is to predict the structural, electronic, and half-metallic ferromagnetic properties of quaternary vanadium fluoride Rb2NaVF6. We have used in our calculation the generalized gradient approximation functional (GGA-PBEsol) [13] and Becke-Johnson exchange potential [14] with Tran-Blaha modified Becke-Johnson (TB-mBJ) potential [15] based on full-potential linearized augmented plane-wave (FP-LAPW) method within first-principle approaches of spin-polarized density functional theory (SPDFT) [16]. This article is redacted as follows: In Sec. 2, we describe the method of the calculation. In Sec. 3, we demonstrate the details of the collected results and discuss the structural, electronic, and magnetic properties of the Rb2NaVF6 compound. Section 4 summarizes the key findings of our current research.
2. Computational method
In this study, we have utilized the FP-LAPW method based on SP-DFT [16] as realized in the WIEN2K software [17,18] to predict the structural, electronic, and magnetic properties of quaternary vanadium fluoride Rb2NaVF6. The structural properties are predicted by applying the GGA-PBEsol [13], while the electronic structures and magnetic properties are calculated with GGA-PBEsol along with TB-mBJ exchange potential. In this study, we have chosen the following calculation parameters: the K max = 9 (RMT)−1 (K max is the plane wave cut-off, and RMT is the smallest of all atomic sphere radii). The Fourier expanded charge density was limited at G max = 12 (Ryd) 1/2 , the l−expansion of the non-spherical potential and charge density was performed up to l max = 10. The cut-off energy is set to -7 Ryd to separate the core from valence states. The muffin-tin radii (MT) for Rb, Na, V and F to be 2.50, 1.98, 1.78 and 1.69 atomic units (a.u.), respectively. The iteration process is repeated until the calculated total energy and charge of the crystal converge to less than 0.0001 Ryd and 0.001e, respectively.
3. Results and discussion
3.1. Stability and structural properties
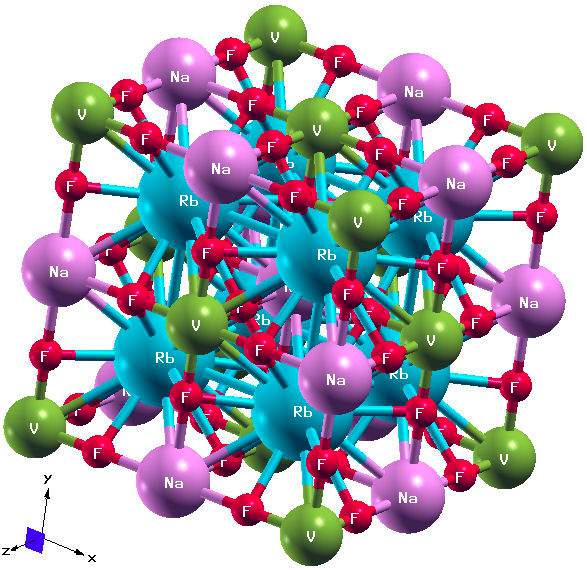
In 1966, R. Hoppe studied the crystallography of the compound
Rb2NaVF6 [19,20]. The quaternary
vanadium fluoride Rb2NaVF6 crystallizes in the cubic NaCl
(B1) structure with a space group of (
TABLE I Rb, Na, V and F atoms positions.
| Atoms | Position | |||
| X | Y | Z | ||
| Rb | Atom 1 | 0.250 | 0.250 | 0.250 |
| Atom 2 | 0.750 | 0.750 | 0.750 | |
| Na | Atom 1 | 0.500 | 0.500 | 0.500 |
| V | Atom 1 | 0.000 | 0.000 | 0.000 |
| F | Atom 1 | 0.230 | 0.000 | 0.000 |
| Atom 2 | 0.770 | 0.000 | 0.000 | |
| Atom 3 | 0.000 | 0.230 | 0.000 | |
| Atom 4 | 0.000 | 0.770 | 0.000 | |
| Atom 5 | 0.000 | 0.000 | 0.230 | |
| Atom 6 | 0.000 | 0.000 | 0.770 | |
TABLE II Calculated lattice constant (a), bulk modulus (B), pressure derivative B’, minimum equilibrium energy E0, and equilibrium volume V0 of Rb2NaVF6.
3.2. Electronic, magnetic properties and half-metallic comportment
In this section, we have predicted the electronic band structure, total (TDOS), and partial (PDOD) densities of states for Rb2NaVF6, using GGA-PBEsol [13] accompanying with (TB-mBJ) of Tran-Blaha modified Becke-Johnson approximation [14,22]. Figures 3 and 4 exhibit the band structure of Rb2NaVF6 for spin-up and spin-down, respectively. It is apparent in Fig. 3 that the highest valence band is above the Fermi level, hence the metallic behavior of the structure. For Fig. 4, we mark two gaps, the half-metallic ferromagnetic gap (G HMF ) and the half-metallic gap (G HM ), G HMF is the energy difference between the valence-band maximum (VBM) and conduction-band minimum (C BM ) [4]. Rb2NaVF6 compound has a direct half-metallic ferromagnetic gap at Γ − Γ of 7.837 eV and large half-metallic gap at Γ−Γ high-symmetry point of 3.582 eV. The non-zero values of the half-metallic gap for Rb2NaVF6 demonstrate it to be true half-metallic ferromagnets and making it promising materials for employment in spintronic applications.
To know the origin of the ferromagnetic and the halfmetallic behavior, we have calculated the densities of states (DOS) around the Fermi level (EF). Fig. 5 shows the total densities of states of Rb2NaVF6, Rb, Na, V, and F atoms. We notice that the total density of states (TDOS) is symmetrical except at Fermi level (0 eV) for spin-up and 3.618 eV for spin-down. The total densities of states are dominated by Rb between the energy from -11.102 and -10.694 eV, and at energy more than 8 eV. While the F dominates at an energy between -6.476 and -4.190 eV. Moreover, V dominates the peaks, which are at the energies 0, 3.618, and 4.380 eV. The half-metallic nature can be seen in the channel spin-down. To comprehend the source of the half-metallic gap and the half-metallic ferromagnetic gap we have plotted the partial densities of states. Figure 6 represent the partial densities of states of Rb2NaVF6, the pike located at the 0 eV (Fermi level) and 3.618 eV are mainly formed by the 3d − t2g (V) and 2p (F) states. The TDOS of Rb2NaVF6 depicted asymmetrical states of spin-up and spin-down due to strong p − d hybridization between the 2p (O) and 3d − t2g (V) states around the Fermi level for the majority-spin direction. This hybridization occurs mainly at the top of the majority-spin valence bands and crosses the Fermi level, leading to the metallic nature for Rb2NaVF6 compounds, with spin polarization of 100% by using the following expression [23]:

FIGURE 5 Spin-polarized total densities of states (TDOS) of Rb2NaVF6. The Fermi level is set to zero. (vertical dotted red line).

FIGURE 6 Spin-polarized partial densities of states (PDOS) of Rb2NaVF6. The Fermi level is set to zero. (vertical dotted red line)
where P is the spin polarization, N ↑
(E
F
) and N ↓ (E
F
) are the densities of states of the majority spin and minority spin
around the Fermi level, respectively. Table
III display the total and local magnetic moments of
Rb2NaVF6. To interpret the implications of the
p−d interchange phenomenon on the magnetic
behavior, we have calculated the total and local magnetic moments of the Rb, Na,
V, and F atoms as well as the interstitial sites. The results exhibit the total
magnetic moment for the Rb2NaVF6 compound was around 2
µB, usually caused by the V atoms’ the local magnetic
moment. 3d (V) majority-spin states, which are partially
occupied with three electrons, resulting in a total magnetic moment of 2
µB. Otherwise, the calculated magnetic moment of the V atom
is reduced to 1.71792 µB and minor local magnetic moments are
induced at Rb, Na, F, and interstitial sites overdue to the p −
d exchange interaction between 2p (F) and
3d − t2g(V) states.
Important parameters established on band structures such as p −
d exchange splitting have also been calculated,
TABLE III Calculated total and local magnetic moments of the relevant Rb, Na, V, and F atoms and in the interstitial sites (in Bohr magneton µB) for Rb2NaVF6.
| Compound | Total (µB) | Rb (µB) | Na (µB) | V (µB) | F (µB) | Interstitial (µB) |
| Rb2NaVF6 | 2.00001 | 0.00018 | 0.00009 | 1.71792 | 0.00495 | 0.25194 |
Both N 0 α and N 0 β parameters are calculated employing the mean-field theory whose expression is as follows [24,25]:
where
4. Conclusion
We have theoretically calculated the structural, electronic, and magnetic properties of the cubic Rb2NaVF6 system, using the density functional theory and it is concluded that:
The lattice constant is in good agreement with the obtainable experimental data.
Rb2NaVF6 is metallic for the majority spin states while semiconducting for the minority spin state with a direct large half-metallic gap of 3.582 eV.
Rb2NaVF6 exhibits 100% spin polarization at the Fermi level (EF).
The Rb2NaVF6 compound can be used in spintronic applications and can operate at a higher temperature due to its half-metallic properties and with a wide bandgap.











 nueva página del texto (beta)
nueva página del texto (beta)