1.Introduction
The information-theoretic measures have received a great research interest in quantum mechanical systems over the years. These are largely due to its applications in probability density function and computation and have provided a broader perspective for various quantum mechanical systems 1-3. The concepts of information-theoretic measures have been applied in areas such as communication 4, physical sciences 5, chemical sciences 6, and other disciplines that have connections with quantum information systems 7-8. Quantum information-theoretic measures quantify uncertainty, and these measures are classified as either global or local measures. The global measures describe the probability density spread in a region 9-10, and these include Shannon entropy 2, Renyi entropy 11, Tsallis entropy 12, and Onicescu information energy 13. On the other hand, the local measure is the Fisher information 14 and is concerned with the point changes that occur in the probability density 15. Quantum information theory is a very important tool in the uncertainty measures of atoms and molecules, and of all these quantum information measures, the Shannon entropy and Fisher information have been exhaustively studied than other information-theoretic tools 2,14. The entropic densities in the position and conjugate momentum spaces provide the basic description of a molecular and chemical system. In the molecular system, it provides a good narrative for chemical bonding 16, and it can also be applied in the comparison of molecular interactions 17-18. Several research works have been carried out for information-theoretic measures both analytically and numerically. For instance, Isonguyo et al.19 investigate the different information-theoretic tools for the screened Coulomb potential. On the other hand Onate et al. 20 investigated the dissociation energy effect on the Shannon entropy and Renyi entropies. Romera et al. 15 studied analytically the behavior of Fisher information for the central potential for a single particle system and established a novel uncertainty relation that is satisfied for any central potential model. Amadi et al. 21 analyzed comparatively the screened Coulomb potential and screened Kratzer potential in three dimensions for Shannon entropy and Fisher Information. Another application of the Fisher information is in the study of the Schrödinger equation in the presence of external electrical and magnetic effects in atomic systems 22. The Shannon and Fisher information has been studied for position-dependent mass within the framework of non-relativistic quantum mechanics 23-25. This study will offer more information in the applications to semiconductors and quantum dots. Information entropies have been investigated for scaling behavior properties 26-28, confined systems 29-32, shape effect of quantum heterostructures 33, among others 34-41. In recent times, there are very little research works on information theory with exponential type potentials, and to the best of our knowledge, no application of diatomic molecules for exponential type potential has been investigated and hence the motivation of this study. The quantum information-theoretic measure considered in this study is the molecular Deng-Fan-Eckart potential model (DFEP). Recently, Edet et al. 42 studied the DFEP model for some selected diatomic molecules. The choice of this potential stems from the fact that it exhibits an almost exact behavior with that of the Morse potential and so makes it a good choice to the study of atomic interaction for diatomic molecules. The organization of the paper is as follows: Section 2 is devoted to the solutions of the Eigen solutions of the DEFP. Section 3 tabulates the spectroscopic values of the diatomic molecules. Section 4 is concerned with the information entropy, where we examine the Shannon entropy and Fisher information. Finally, we give a brief conclusion in Sec. 5.
2.Eigensolution of DFEP
The Deng-Fan-Eckart potential is defined as 42,
where,
where,
Other parameters are defined in Ref. 42,
where,
and
The momentum-space wave function is obtained by taking the Fourier transformation 48 of the position space wave function. For the ground state, the momentum space wave function is given as,
where,
However, due to the difficulty and complexity of the integral expression in the momentum state at the first excited state, we solved for the first excited state in position and momentum spaces numerically.
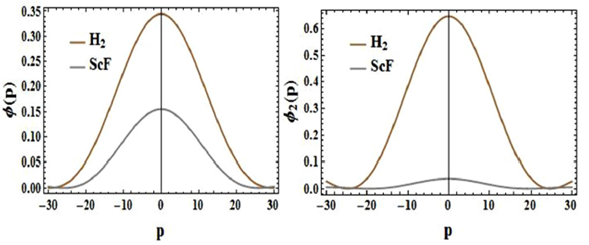
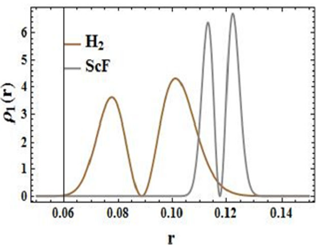
Figures 1 and 2 shows the characteristic behaviors of the probability densities, which are plotted in position and momentum space, respectively. From the plots, we observed that ScF is more concentrated than H2 and so shows a higher localization.
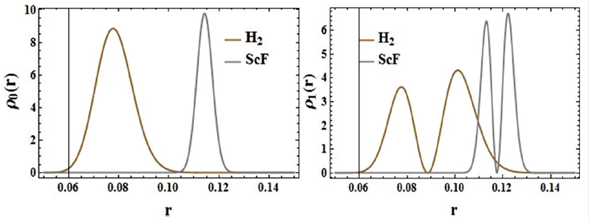
Figure 1 Probability densities in the position space for the selected diatomic molecules at the ground and excited state for l = m = 0.
3.Spectroscopic values for some diatomic molecules
Many interesting studies have been investigated on Shannon entropies and Fisher information with different potential models in recent times 50-53. Here, we intend to study the quantum information -theoretic measures for the diatomic molecules of H2 and ScF. These selected diatomic molecules are homonuclear and heteronuclear, respectively. These diatomic molecules possess the same properties as each diatomic molecule is made of two atoms only and differ from each other in terms of covalent bonding and their geometric structure 54,55. Our choice of these two molecules is based on the available data of their spectroscopic parameters as given in Table I. Hence, we intend to observe their quantum measures in the study. We take the experimental values of the spectroscopic parameters for each of the diatomic molecules from Ref. 42.
4.Information entropies
4.1Shannon entropy
In this section, the quantum information-theoretic measures for Shannon entropy and Fisher information in position and momentum spaces will be calculated. Shannon entropy, which is regarded as a logarithmic probability density, investigates the concentration of the probability densities spread in a quantum system. It is defined for position and momentum spaces in spherical polar coordinate as 30;
where Sr, Sp, and
where, D is the spatial dimension.
Tables II and III show the numerical results for the Shannon entropies of the two diatomic molecules of and ScF for the ground and excited states in the position and momentum spaces. In Table II, we observed that the Shannon entropies in the position space are all negative in the ground and excited state. This behavior of the negative Shannon entropic value shows that the position Shannon entropy has a characteristic of a high localization 19, which implies a high accuracy in the prediction of the localization and less uncertainty. More so, in the first excited state, there is a decrease in the Shannon entropy values in the position space, which reaffirms its delocalization of H2 diatomic molecules. Similarly, in Table III, high localization is observed for ScF diatomic molecule in the position space as its Shannon entropy values dropped for increasing angular momentum quantum number l. In the momentum space, we observed a decreasing Shannon entropic value for both diatomic molecules at the first excited state, and hence there is an occurrence of localization for the two diatomic molecules. Subsequently, the computed Shannon entropies in the position and momentum spaces for the two diatomic molecules satisfied the BBM uncertainty relation.
Table II Shannon entropy in the position space for H2 diatomic molecules
| n | l | Sr | Sp | Sϕ,θ | St |
| 0 | 0 | -8.5615577582 | 12.0463422727 | 2.5310242469 | 53.7013355814 |
| 0 | -8.2329583587 | 13.9224628761 | 2.5310242469 | 67.5539999101 | |
| 1 | 1 | -8.2238032731 | 13.9136537663 | 2.0990786246 | 62.1281849644 |
4.2.Fisher information
On the other hand, the Fisher Information is a local measure of information entropy and has a differential component which makes it very sensitive to detect local changes that occur in the probability density. Fisher information, usually regarded as the measure of information entropy 14,38, is the control of localization of the probability density. It can be seen as a measure of oscillator degree, which has applications in quantum mechanical kinetic energy of the system 54. Thus, Fisher information in position space and momentum space is expressed as 14,38
In the theory of Fisher information, the higher the Fisher information, the higher the accuracy of predicting the localization of the system and thus increasing the Fisher information increased the fluctuation of the system. Generally, for an arbitrary angular momentum quantum number l of any central potential model, the two products of the Fisher information must satisfy the the Stam, Cramer-Rao inequality 15,
where
In Tables IV, we compute numerically the Fisher information in the position and momentum spaces for the diatomic molecules of H2 and ScF at the ground and excited states for different quantum numbers. We observed that the Fisher information values increase as it transits from the ground state to the excited state. At the excited state, Fisher information decreases as the orbital angular momentum quantum l is increased. This behavior is observed for the two diatomic molecules, which indicate the presence of fluctuation and delocalization in the diatomic molecules. Finally, the Stam-Cramer-Rao inequality relation is satisfied for the two diatomic molecules.
5.Conclusions
In this work, we have studied the quantum information measures for Shannon entropy and Fisher information for the two selected diatomic molecules of H2 and ScF in the position and momentum spaces numerically at the ground and first excited states. Each diatomic molecule investigated satisfied the BBM inequality for the Shannon entropy and Stam-Cramer-Rao inequality relation for the Fisher information. In this study, we have shown that H2 that ScF satisfied the uncertainty relations for Shannon and Fisher information at the ground and excited states.
6.Graphical abstract text and image
In this study, the Shannon entropy and Fisher information is investigated with molecular Deng-Fan-Eckart potential for the diatomic molecules H2 and ScF in position and momentum spaces in three dimensions. Localization is observed for the Shannon entropy and delocalization for the Fisher information for the two diatomic molecules considered in position and momentum spaces. The Shannon entropy and the Fisher information measures for the two diatomic molecules satisfied the Bialynicki-Birula and Mycielski (BBM) and the Stam-Cramer-Rao inequalities uncertainty relation respectively.











 nueva página del texto (beta)
nueva página del texto (beta)