1.Introduction
The solutions of the radial Schrödinger equation is of immense importance in nonrelativistic quantum mechanics because it is well established that the wave function contains all the necessary information required to describe a quantum system 1-3. From the early days of quantum mechanics, the study of exactly solvable problems has attracted considerable attention in many branches of physics. In particular, the applications of quantum mechanics to nuclear physics, information theory, molecular physics, and particle physics need not be overemphasized 4,5.
It is well known that exact solutions of this equation are only possible for a few
potential models, such as the Kratzer 6-7, Eckart potential 8-10, shifted Deng-Fan 11-14, Molecular Tietz potential 15-18, etc. The exact analytical solutions of the
Schrödinger equation with some of these potentials are only possible for
The trigonometric Pöschl-Teller potential was proposed by Pöschl and Teller 50 in 1933, and it has been used in describing diatomic molecular vibration. This potential can be written as
where parameters V1 and V2 describe the property of the potential well, whereas the parameter α is related to the range of this potential 51.
This potential has been applied to study diatomic molecular vibration. Ever since it was proposed in 1933, researchers have given much attention to the molecular potential. For example, Liu et al.51 carried out a fermionic analysis with this potential. The bound state solutions have also been carried out in the relativistic regime by Falaye and Ikhdair 52, Chen 53, Candemir 54. and Hamzavi 55.
Very recently, Hamzavi and Rajabi 56 also studied the s-wave solutions of the Schrödinger
equation for this potential using the Nikiforov-Uvarov method. Hamzavi and Ikhdair
57 obtained the approximate
solutions of the radial Schrödinger equation for the rotating trigonometric PT
potential using the Nikiforov-Uvarov method. The energy eigenvalues and their
corresponding eigenfunctions were calculated for arbitrary
Motivated by Ref. 50-57, we propose a modification to the trigonometric Pöschl-Teller potential, called the Generalized trigonometric Pöschl-Teller potential. This potential is given as:
where parameters V1, V2, V3, and V4 describe the property of the potential well, whereas the parameter α is related to the range of this potential. For what obtains in previous studies of the molecular potential, we modified the potential to allow for more physical application and comparative analysis to existing studies of the molecular potential. Besides, in molecular physics, it has also been established that potential energy functions with more parameters tend to fit experimental data than those with fewer parameters, and researchers have recently paid great attention to obtaining modified version of potential functions by employing dissociation energy and equilibrium bond length for molecular systems as explicit parameters. This model will be an important tool for spectroscopists to represent experimental data, verify measurements, and make predictions.
The first step in obtaining the thermodynamics properties of a given system is to calculate its vibrational partition function. The partition function, which explicitly depends on temperature, aids us to obtain other thermodynamics properties. The vibrational partition function for certain potential models can easily be obtained by calculating the rotation-vibrational energy levels of the system whose applications are widely used in statistical mechanics and molecular physics 58,59. Different mathematical approaches have been employed by many researchers in evaluating partition functions, such as Poisson the summation formula 60, commulant expansion method 61, standard method 62, and Wigner-Kirkwood formulation 63. Superstatistics is the topic of interest in statistical mechanics.
Superstatistics is a superposition of different statistics: One given by ordinary Boltzmann factor and another given by the fluctuation of the intensive parameter such as the inverse temperature. Superstatistics describe non-equilibrium systems with a stationary state and intensive parameter fluctuations and contains Tsallis statistics as a special case 64-72.
Therefore, it is the primary objective of the present work to study the Schrödinger equation for non-zero angular momentum with the generalized trigonometric Pöschl-Tellerpotential using the Functional Analysis Approach. We will also use the resulting energy equation to find the partition function, which will enable us to calculate other thermodynamics properties via statistical mechanics and superstatistics mechanics approach.
This paper is organized as follows. In Sec. 2, we derive the bound states of the Schrödinger equation with the generalized trigonometric PT potential using the FAA. In Sec. 3, we obtain the thermodynamic properties, which will be calculated using the expression for the partition function. In Sec. 4, we calculate the effective Boltzmann factor considering modified Dirac delta distribution in the deformed formalism. We obtain the statistical properties of the systems by using the superstatistics. In Sec. 5, we obtain the rotational-vibrational energy spectrum for some diatomic molecules with numerical results and discussion. In Sec. 6, we present special cases of the potential under consideration. Finally, in Sec. 7, we give a concluding remark.
2.Energy levels and wavefunctions
The radial part of the Schrödinger equation is given by 60;
Considering the generalized trigonometric Pöschl-Teller potential (Eq. (2)), we obtain the radial Schrödinger equation, Eq. (3) is rewritten as follows:
This equation cannot be solved analytically for
where d0 = 1/12 is a dimensionless shifting parameter, and α is the screening parameter. It is noted that for a short-range potential, the relation Eq. (5) is a good approximation to 1/r2 as proposed by Greene and Aldrich 19,53 approximation. This implies that Eq. (5) is not a good approximation to the centrifugal barrier when the screening parameter becomes large. Thus, the approximation is valid when αr=1.
Inserting Eqs. (5) into Eq. (4), we have:
Using the coordinate transformation
For Mathematical simplicity, let us introduce the following dimensionless notations:
To solve Eq. (6), we propose the physical wave function as:
where
and
On substitution of Eq. (9) into Eq. (7) leads to the following hypergeometric equation:
whose solutions are the hypergeometric functions
where
By considering the finiteness of the solutions, the quantum condition is given by
from which we obtain, the energy expression as
Thus, if one substitutes the value of the dimensionless parameters in Eq. (8) into Eq. (16), we obtain the energy eigenvalues as:
The corresponding unnormalized wave function is obtained as
where
Putting Eq. (18) into the Eq. (19) yields
where
The integral I
n
is calculated for different n values using the Mathematica software program
for
Hence, we find
By using Eqs. (23) and (18) one can plot the radial wave functions for arbitrary quantum states through the Mathematica software program.
3.Thermal Properties of generalized trigonometric Pöschl-Teller potential
We consider the contribution of the bound state to the vibrational partition function at a given temperature T 58,60
Here, kB is the Boltzmann constant, and
We can rewrite Eq. (17) to be of the form
where
We substitute Eq. (25) into Eq. (24) to have
where
Replacing the sum in Eq.(27) by an integral in the classical limit, we obtain
where
Therefore, we use the mathematica software to evaluate the integral in Eq. (29), thus obtaining the partition function for generalized trigonometric Pöschl-Teller potential model.
The imaginary error function can be defined as 62
Thermodynamic functions such as; free energy, entropy, internal energy, and specific heat capacity functions can be obtained from the partition function (31) as follows 20.
3.1.Helmholtz free energy
3.2.Entropy
where
4.Superstatistics mechanics
In this section, we introduce the necessary conditions of superstatistics. The effective Boltzmann factor of the system can be written as 73,74
where
is the probability density. Besides we state here the modified form of Dirac delta function used in this study as 75:
Finally, we find the generalized Boltzmann factor as in Ref. 75
where 𝑞 is the deformation parameter. Details of Eq. (39) can be found in Appendix A of Ref. 75 and references therein.
The partition function for the modified Dirac delta distribution has the following form 75:
We substitute Eq. (25) into Eq. (40) to have
Therefore, we use Mathematica software to evaluate the integral in Eq. (41), thus obtaining the partition function with generalized trigonometric Pöschl-Tellerpotential model in superstatistics as follows:
where
Other thermodynamic functions such as Helmholtz free energy, FS(β), entropy, SS(β), internal energy, US(β), and specific heat, CS(β), functions can be obtained from the partition function (42a) as follows:
4.1.Helmholtz free energy
The Helmholtz free energy is obtained in superstatistics formalism with the aid of Eq. (33a) as follows:
where
4.2.Entropy
The entropy is obtained in superstatistics formalism with the aid of Eq. (34a) as follows:
where
4.3.Internal energy
The internal energy is obtained in superstatistics formalism with the aid of Eq. (35a) as follows:
4.4.Specific heat capacity
The specific heat is obtained in superstatistics formalism with the aid of Eq. (36a) as follows:
where
5.Numerical results and applications
To show the accuracy of our work, we calculate the energy eigenvalues using Eq. (18)
for different quantum numbers n and
Table I Bound state energy levels Enf for the Generalised trigonometric Pöschl-Teller potential obtained with parameters V1 = 5 f m−1, V2 = 3 f m−1, V3 = 0.5, V4 = 0.5, and µ = 10 f m−1
| States | α = 0.002 | α = 0.02 | α = 0.2 | α = 0.4 | α = 0.8 | α = 1.2 |
| 1s | 18.50038334 | 18.61121709 | 19.73743352 | 21.0271324 | 23.72899708 | 26.59648864 |
| 2s | 18.50858178 | 18.69348948 | 20.58899614 | 22.79449204 | 27.52159072 | 32.67406160 |
| 2p | 18.50858258 | 18.69357133 | 20.59752395 | 22.83011829 | 27.67609429 | 33.04821322 |
| 3s | 18.51678180 | 18.77592188 | 21.45655875 | 24.62585164 | 31.57018435 | 39.32763454 |
| 3p | 18.51678262 | 18.77600388 | 21.46523908 | 24.66269723 | 31.73441612 | 39.73447216 |
| 3d | 18.51678425 | 18.77616788 | 21.48259499 | 24.73630368 | 32.06125854 | 40.53875474 |
| 4s | 18.52498345 | 18.85851426 | 22.34012135 | 26.52121126 | 35.87477799 | 46.55720749 |
| 4p | 18.52498425 | 18.85859642 | 22.34895421 | 26.55927615 | 36.04873794 | 46.99673112 |
| 4d | 18.52498588 | 18.85876072 | 22.36661499 | 26.63531596 | 36.39487055 | 47.86516178 |
| 4f | 18.52498834 | 18.85900721 | 22.39309395 | 26.7491527 | 36.90974960 | 49.14313806 |
Table II Comparison of s-wave energy eigenvalues (in eV) obtained by using the Functional Analysis Approachwith other methods for the trigonometric Pöschl-Teller potential with other methods obtained with parameters V1 = 5 f m−1, V2 = 3 f m−1, and µ = 10 f m−1.
| n | Present | AIM [64] | NU [56] | Present | AIM [64] | NU [56] | Present | AIM [64] | NU [56] |
| α= 0:2 | α= 0:2 | α= 0:02 | α= 0:02 | α= 0:002 | α= 0:002 | ||||
| 0 | 16.10494172 | 16.104 941 73 | 16.104 941 72 | 15.78149898 | 15.781 498 98 | 15.781 498 98 | 15.7495163 | 15.749 516 29 | 15.749 516 29 |
| 1 | 16.83082621 | 16.830 826 21 | 16.830 826 21 | 15.8526429 | 15.852 642 89 | 15.852 642 89 | 15.75661628 | 15.756 616 28 | 15.756 616 28 |
| 2 | 17.5727107 | 17.572 710 70 | 17.572 710 70 | 15.9239468 | 15.923 946 80 | 15.923 946 80 | 15.76371788 | 15.763 717 86 | 15.763 717 86 |
| 3 | 18.33059519 | 18.330 595 18 | 18.330 595 18 | 15.99541072 | 15.995 410 71 | 15.995 410 71 | 15.77082105 | 15.770 821 05 | 15.770 821 05 |
| 4 | 19.10447968 | 19.104 479 67 | 19.104 479 67 | 16.06703462 | 16.067 034 63 | 16.067 034 63 | 15.77792584 | 15.777 925 84 | 15.777 925 84 |
| 5 | 19.89436415 | 19.894 364 16 | 19.894 364 16 | 16.13881855 | 16.138 818 54 | 16.138 818 54 | 15.78503222 | 15.785 032 22 | 15.785 032 22 |
| 6 | 20.70024864 | 20.700 248 64 | 20.700 248 64 | 16.21076245 | 16.210 762 45 | 16.210 762 45 | 15.79214021 | 15.792 140 21 | 15.792 140 21 |
Table III Comparison of s-wave energy eigenvalues (in eV) obtained by using the Functional Analysis Approach with other methods for the trigonometric Pöschl-Teller potential with other methods obtained with parameters V1 = 5 f m−1, V2 = 3 f m−1, and µ = 10 f m−1.
| n | Present | NU [56] α = 1.2 | Present | NU [56] α = 0.8 | Present | NU [56] α = 0.4 |
| 0 | 18.02560022 | 18.02560022 | 17.23163309 | 17.23163309 | 16.47211972 | 16.47211973 |
| 1 | 22.87051711 | 22.8705171 | 20.32991862 | 20.32991862 | 17.95616358 | 17.95616357 |
| 2 | 28.29143400 | 28.29143398 | 23.68420415 | 23.68420415 | 19.50420741 | 19.50420742 |
| 3 | 34.28835088 | 34.28835086 | 27.29448969 | 27.2944896 | 21.11625128 | 21.11625126 |
| 4 | 40.86126776 | 40.86126774 | 31.16077521 | 31.16077522 | 22.79229512 | 22.7922951 |
| 5 | 48.01018464 | 48.01018462 | 35.28306075 | 35.28306074 | 24.53233896 | 24.53233894 |
| 6 | 55.73510152 | 55.7351015 | 39.66134628 | 39.66134628 | 26.33638282 | 26.33638278 |
Table IV Comparison of l-state energy eigenvalues (in eV) obtained by using the Functional Analysis Approach with other methods for the trigonometric Pöschl-Teller potential with other methods obtained with parameters V1 = 5 f m−1, V2 = 3 f m−1, and µ = 10 f m−1.
| States | Present | NU [57] α = 1.2 | Present | NU [57] α = 0.8 | Present | NU [57] α = 0.4 | Present |
| 1s | 22.87051711 | 22.87051710 | 20.32991862 | 20.32991862 | 17.95616358 | 17.95616357 | 16.83082621 |
| 2s | 28.29143400 | 28.29143398 | 23.68420415 | 23.68420415 | 19.50420741 | 19.50420742 | 17.57271070 |
| 2p | 28.64395420 | 28.64395419 | 23.82847893 | 23.82847894 | 19.53712285 | 19.53712286 | 17.58054181 |
| 3s | 34.28835088 | 34.28835086 | 27.29448969 | 27.2944896 | 21.11625128 | 21.11625126 | 18.33059519 |
| 3p | 34.67512504 | 34.67512504 | 27.44896379 | 27.44896381 | 21.15044541 | 21.15044543 | 18.33858624 |
| 3d | 35.43921159 | 35.43921159 | 27.75631555 | 27.75631556 | 21.21875332 | 21.2187533 | 18.35456400 |
| 4s | 40.86126776 | 40.86126774 | 31.16077521 | 31.16077522 | 22.79229512 | 22.7922951 | 19.10447968 |
| 4p | 41.28229588 | 41.28229584 | 31.32544867 | 31.32544868 | 22.82776799 | 22.8277680 | 19.11263069 |
| 4d | 42.11348591 | 42.11348590 | 31.65300784 | 31.65300783 | 22.89862722 | 22.89862721 | 19.12892818 |
| 4f | 43.33519178 | 43.33519178 | 32.14003976 | 32.14003977 | 23.00470172 | 23.00470171 | 19.15336296 |
Table V Comparison of l-state energy eigenvalues (in eV) obtained by using the Functional Analysis Approach with other methods for the trigonometric Pöschl-Teller potential with other methods obtained with parameters V1 = 5 f m−1, V2 = 3 f m−1, and µ = 10 f m−1.
| States | Present | NU [57] α = 0.2 | Present | NU [57] α = 0.02 | Present | NU [57] α = 0.002 |
| 1s | 16.83082621 | 16.83082621 | 15.8526429 | 15.85264289 | 15.75661628 | 15.75661628 |
| 2s | 17.5727107 | 17.5727107 | 15.9239468 | 15.9239468 | 15.76371788 | 15.76371786 |
| 2p | 17.58054181 | 17.58054181 | 15.92402152 | 15.92402153 | 15.76371861 | 15.76371860 |
| 3s | 18.33059519 | 18.33059518 | 15.99541072 | 15.99541071 | 15.77082105 | 15.77082105 |
| 3p | 18.33858624 | 18.33858626 | 15.99548559 | 15.9954856 | 15.77082179 | 15.77082179 |
| 3d | 18.35456400 | 18.35456399 | 15.99563535 | 15.99563534 | 15.77082329 | 15.77082328 |
| 4s | 19.10447968 | 19.10447967 | 16.06703462 | 16.06703463 | 15.77792584 | 15.77792584 |
| 4p | 19.11263069 | 19.1126307 | 16.06710967 | 16.06710967 | 15.77792658 | 15.77792658 |
| 4d | 19.12892818 | 19.12892817 | 16.06725975 | 16.06725974 | 15.77792808 | 15.77792806 |
| 4f | 19.15336296 | 19.15336297 | 16.06748486 | 16.06748485 | 15.77793030 | 15.77793030 |
In Fig. 1a) and b), we plot the shape of the potential for clarity and understanding of the system we are studying. Figure 1a) we plot the shape of the generalized trigonometric Pöschl-Tellerpotential against the interatomic distance. Figure 1b) shows a comparative plot of the shapes of the trigonometric Pöschl-Tellerpotential model and generalized trigonometric Pöschl-Tellerpotential. However, we note that our generalized model fits appropriately with the trigonometric Pöschl-Tellerpotential.
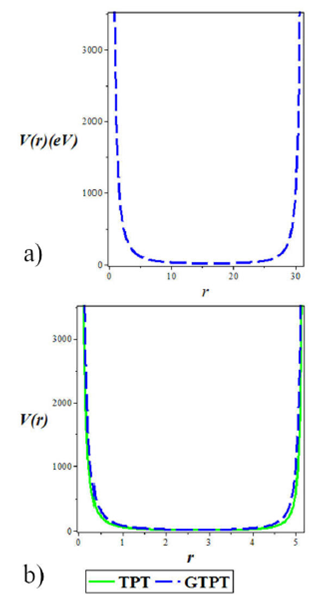
Figure 1 a) Shape of the generalized trigonometric Pöschl- Tellerpotential for different values of the screening parameter a. We chose V1 = 5 f m-1 , V2 = 3 f m-1 , V3 = 2 f m-1 , and V4 = 0:5 f m-1 . b) Shape of the trigonometric Pöschl-Tellerpotential model and generalized trigonometric Pöschl-Tellerpotential. We chose V1 = 5 f m-1 , V2 = 3 f m-1 , V3 = 2 f m-1 , V4 = 0:5 f m-1 , and a = 0:3.
Figures 2 a)-f) clearly shows the energy
eigenvalues variation with parameters V1, V2, V3,
V4, μ and α for various quantum states. It can be easily observed
from these Figs. 2a)-d) that the parameters increase directly as the energy
increases. Figure 2e) shows the energy
eigenvalues variation with the particle’s reduced mass μ for different quantum
states. It is seen that in the region
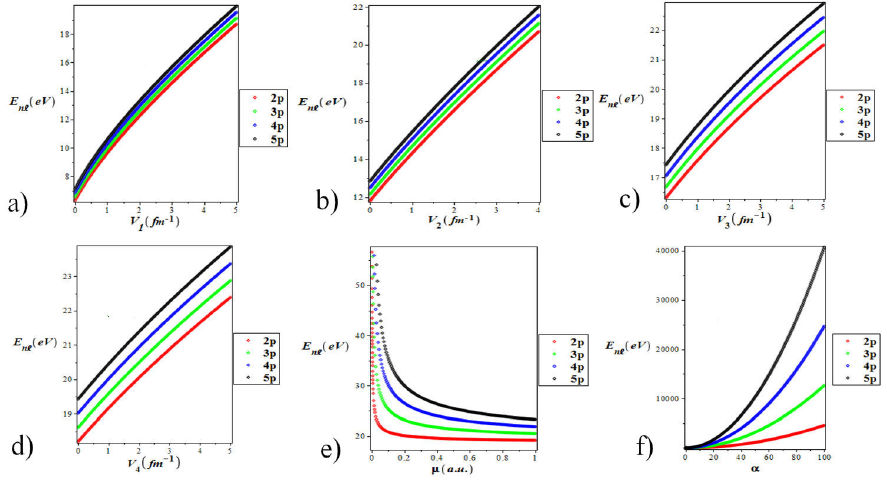
Figure 2 Energy eigenvalues variation with (a) parameter for various quantum states (b) parameter for various quantum states. (c) with parameter for various quantum states. (d) with parameter for various quantum states (e) with particle’s mass for various quantum states. (f) with screening parameter for quantum states.
In Figs. 3a)-e), we show a graphical representation of the thermal properties obtained via the standard Boltzmann-Gibbs statistical mechanical approach. We analyze how these properties vary with β for different discrete values of nmax. Figure 3(a) shows the partition function variation with β for various values of nmax. It can be seen that the partition function decreases as the temperature increases. It is also shown that in the high temperature limits, there’s a uniform convergence of all the curves and the partition function reaches its minimum. Figure 3(b) shows the mean free energy variation with β for different values of nmax. Again, it is seen that the free energy reduces monotonically with β. Figure 3(c) shows the entropy variation with β for different values of nmax. It is seen that the entropy declines as temperature increases. Figure 3(d) shows the mean energy variation with β for various values of nmax. The mean energy decreases as β increases. It is also observed that the mean energy has its minimum in the high β region. Figure 3(e) clearly shows the specific heat capacity variation with β for different values of nmax. An asymmetric shaped formed for increasing value of nmax. At nmax = 300, its trough is reached and heat capacity monotonically growth with β. We see that at some point in β, the values of nmax might become invariant.
In Fig 4(a-e), we graphically display the thermal properties obtained via the standard Boltzmann-Gibbs statistical mechanical approach. We analyze how these properties vary with nmax for different values of β. Figure 4a) clearly shows the Partition Function variation with nmax for various values of β. From this plot, we observe that there is spread from the zero point; the partition function increases as nmax increases. It is also observed that the partition function has its maximum in the high region of nmax. Figure 4b) clearly shows the free energy variation with 𝑛 max for different values of β. It is clearly shown that the mean free energy rises logarithmically as nmax rises. Figure 4c) shows a plot of entropy variation with different values of β. It is seen that the entropy up-surges monotonically with nmax. Figure 4d) displays the plot of mean energy variation with nmax for different values of β. The mean energy surges in an linear-monotonic pattern. Figure 4e) presents the plot of specific heat capacity variation with nmax nmax for different values of β. As predicted in Fig. 3e), it clearly shows for the different values of β, at some point in nmax, heat capacity becomes invariant. We can deduce that for the values of nmax, specific heat and β is invariant.
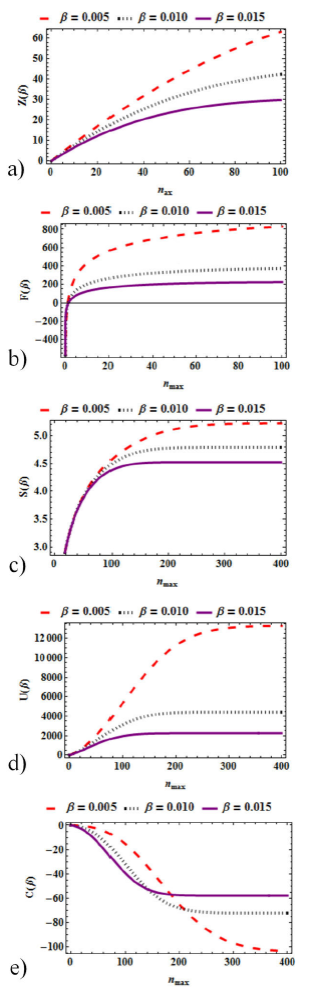
Figure 4 a) Partition Function variation with nmax for various values of β. b) Free energy variation with nmax for different values of β. c) Entropy variation with nmax for different values of β. d) Mean energy variation with nmax for different values of β. e) Specific heat capacity variation with nmax for different values of β.
In Fig 5(a-e), we show graphically the thermal properties obtained via the superstatistical mechanical approach. We analyze how these properties vary with β for different values of the deformation parameter q. Figure 5a) shows a plot of the partition function variation with β for various values of q. It is seen that the partition function decreases as β increases. More so, the partition function increases as q increases. Figure 5b) shows the variation of mean free energy with β for various values of q . The mean free energy decreases monotonically as β increases. A plot of entropy variation with β for different values of q is shown in Fig. 5c). The entropy of the system reduces as β rises. For different values of the deformation parameter, q, the entropy of the system increases with increasing 𝑞. Figure 5d) shows the variation of the mean energy with β for various values of q. The mean energy decreases with increasing β and increases with increasing q. Figure 5e) depicts a plot of specific heat capacity variation with β for different values of q. It is seen explicitly that the specific heat capacity of the system increases monotonically with increasing β but decreases with increasing q.
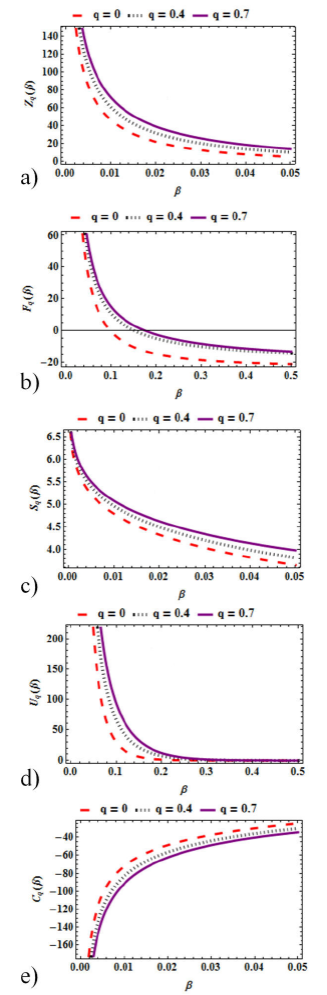
Figure 5 Superstatistics plots of: a) Partition Function variation with β for various values of q. b) Free energy variation with β for different values of q. c) Entropy variation with β for different values of q. d) Mean energy variation with β for different values of q. e) Specific heat capacity variation with β for different values of q.
It is interesting to note also that when q = 0, normal statistics or the conventional Boltzmann-Gibbs statistics is recovered from the superstatistics. However, to further strengthen this claim. We show a graphical comparative plot in Figs. 6a)-e) of all thermal properties obtained via the superstatistics at q = 0 and B-G statistics at maximum quantum number. It is interesting to see that there’s no discernable difference in the curves as they’re both adequately fitted.
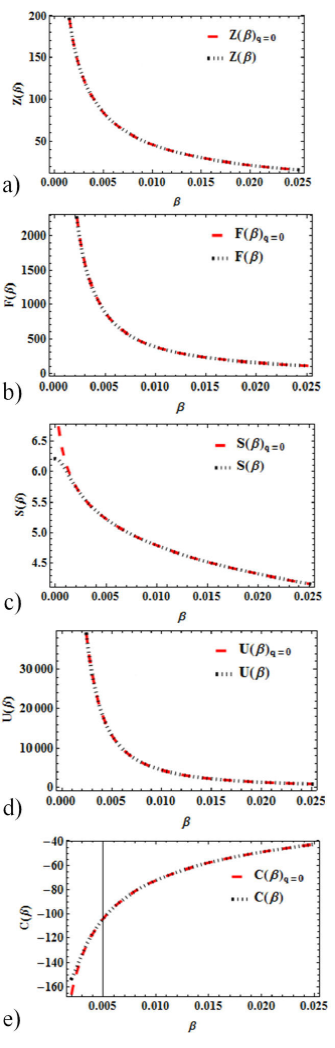
Figure 6 Comparison of superstatistics at q = 0 and normal statistics; a) Partition Function variation with β. b) Free energy variation with β. c) Entropy variation with β. d) Mean energy variation with β. e) Specific heat capacity variation with ¯.
The shape of the radial wave functions is shown in Fig. 7 for 2p, 3d, and 4f quantum states. If we examine the shapes of Fig. 7 carefully, we see that the wave functions have different number of radial nodes and different amplitudes.
6.Special Cases
In this section, we shall study one special case of the Generalized Trigonometric Pöschl-Teller potential and its energy eigenvalues, respectively
6.1.Trigonometric Pöschl-Teller potential
Choosing V3 = V4 = 0, the Generalized Trigonometric Pöschl-Tellerpotential takes 76,56
and the energy eigenvalue becomes
This is in excellent agreement with Eq. (3) of Ref. 76 and Eq. (19) of Ref. 57.
By setting
This is in excellent agreement with Eq. (15) of Ref. 56.
7.Conclusion
In this article, we have solved the Schrödinger equation using the Functional
Analysis Approach and suitable approximation to overcome the centrifugal barrier. We
have also presented the rotational-vibrational energy spectra with the Generalized
Trigonometric Pöschl-Teller potential. We have expressed the solutions by the
generalized hypergeometric functions 2F1(a,b,cp). Results have
been discussed extensively using plots. We discussed some special cases by adjusting
the potential parameters and compute the numerical energy spectra for the
trigonometric Pöschl-Teller potential for both the











 nueva página del texto (beta)
nueva página del texto (beta)





