1.Introduction

Fractional calculus has several applications in science and engineering. Fractional-order modeling has proved to be beneficial, particularly for systems where memory or hereditary properties play a significant role. This is the main advantage of fractional calculus in comparison with the ordinary calculus models in which such effects are in fact neglected. The recent investigations of application of fractional calculus were published in different areas (22),(27). The popularity of fractional calculus is due to the variety of the fractional derivative operators such as Caputo fractional derivative ²⁶, Caputo-Fabrizio fractional derivative ²³, Atangana-Baleanu fractional derivative ²⁴, fractal-fractional derivative ²⁵.

Several applications of fractional calculus for electromagnetism can be found in the literature ^1-3. For example, the fractional curl operator and the fractional paradigm in electromagnetic theory were introduced in ⁴. The application of the fractional curl operator to electromagnetic problems is discussed in Ref. ⁵. In Ref. ⁶, a generalization of vector calculus for a non-integer dimensional space using a product measure approach is presented. The integration over non-integer-dimensional spaces is considered and differential operators of first and second orders for fractional space and non-integer dimensional space are suggested. Gómez et al.²¹ described the fractional space-time electromagnetic waves in dielectric media, for these representations the dimensionality of the ordinary derivative operator was analyzed in order to include it into a fractional derivative operator. Recently, Kachhia and Atangana ¹³ interpret the electromagnetic waves by a fractional derivative of variable and constant order with non-singular kernel. Recently, Gómez et al.²¹ suggested an alternative representation in the Caputo sense for the fractional waves in dielectric media. The authors considered source-free Maxwell equations in isotropic and homogeneous dielectric medium. Other applications of fractional calculus in electromagnetic theory are given in ^7-9.

The generalized Caputo fractional derivative is introduced by Katungampola ¹⁰. Sene and Gómez-Aguilar ¹² have studied the analytical solutions of the electric circuits described by Caputo generalized fractional derivatives. Sene ¹¹ has obtained both an analytic and a numerical solution for certain generalized fractional diffusion equations. In the aforementioned work, the jump from ordinary to fractional derivatives is direct albeit the physical parameters used for the differential equations have different physical dimensions.

In this article, we study some fractional differential equations arising in electromagnetism more precisely. We solve the electromagnetic waves in a plasma and an oscillating electric field. The paper is organized as follows: In Sec. 1, we present the basic details regarding the generalized Caputo fractional derivative. Section 2 deals with an analysis of fractional modelling of electromagnetic waves in plasma under various conditions and finally, in Sec. 3, we present an analysis of electromagnetic waves in dielectric using the new differential operator under different instances.

Definition 1.1 The generalized fractional integral of order α of a continuous function f:[0,+∞]→R is defined in ²⁹ as

where Γ(⋅) denotes the gamma function, p > 0, t > 0 and 0<α<1.

Definition 1.2 The left generalized fractional derivative of the order α of a continuous function f:[0,+∞]→R is defined in ²⁹ as

where Γ(⋅) denotes the gamma function, p > 0, t > 0 and 0<α<1.

Definition 1.3 The Caputo generalized fractional derivative of order α of a continuous function f:[0,+∞]→R is defined in ²⁹ as

where ρ>0,t>0,γ=t1-ρ(d/dt) and 0<α<1.

The Caputo fractional derivative explains the memory effect, while the characteristics of the Caputo generalized fractional derivative is highly affected by the value of 𝜌, so it provides a new direction for the control applications.

Definition 1.4 The ρ-Laplace transform of a continuous function f:[0,+∞]→R is defined in ²⁹ as

The ρ-Laplace transform of the Caputo generalized fractional derivative of a continuous function 𝑓 is given in ²⁹ as

Definition 1.5 The genearlized Mittag-Leffler function is defined in ¹⁵ as

where α>0,β>0 and in particular Eα,1(z)=Eα(z).

2.Fractional modelling of electromagnetic waves in Plasma

Consider absolutely ionized gasoline; this type of fuel is, in physical terms, a hydrogen plasma with an equal amount of electrons and protons. The hydrogen plasma is considered as a uniform slab of plasma of thickness L in the x direction and having very large dimensions in the y and z dimensions. We take proton mass to be effectively infinite compared to the electron mass and the positive charges are therefore effectively fixed in a place. Suppose that we displaced the electrons from the protons by a distance x≪L. An electric field is set up that would exert a force on the electrons, pulling them back to the protons. Letting the electrons run, they would rush again in the direction of the protons, overshoot and an oscillations could be set up with a feature frequency ¹⁴. We will develop a simple model, i.e. we regard the medium as an electric (restoring) force, -kx(t)=4πne2x(t), is produced in the direction of equilibrium position. The equation of motion of each electron is therefore

where -nel is the charge per unit area the force per unit area is F=-4πn2e2Lx, and the mass per unit area is nmeL. Equation (7) corresponds to a harmonic oscillator with a frequency

called the electron plasma frequency.

2.1.Zero electric fields

Let us consider Eq. (7) with the Caputo generalized fractional derivative in following way

1σ21-vGCDt2α,ρxt+4πne2mext=Et,0<α≤1,ρ>0 (9)

The auxiliary parameter σ2(1-ν) is introduced with the finality to keep consistency with the dimensionality of the fractional differential equation; here σ has dimensions of time (in seconds) ³⁰.

Consider E(t) = 0, x(0) = x₀, ẋ(0)=0

GCDt2α,ρx(t)+ω2x(t)=0, (10)

where

ω2=4πne2σ2(1-ν)me=ω02σ2(1-ν), (11)

is the fractional electron plasma frequency for different value of v. Applying p-Laplace transform of Eqs. (5)-(10) and considering x(0) = x₀ and ẋ(0)=0, yields

s2αx¯(s)-s2α-1x0+ω2x¯(s)=0, (12)

and by simplifying the above equation, we have

x¯(s)=s2α-1s2α+ω2x0 (13)

As derived in ¹², Eq.(13) gives

x(t)=x0E2α-ω2tρρ2α. (14)

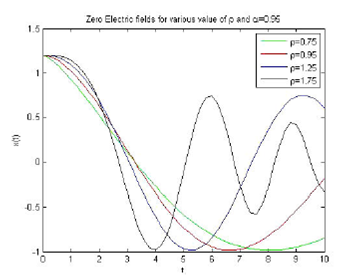
Figures 1 and 2 show the behavior of wave solutions to Eq. (14) for a zero electric field in a plasma for different values of the parameters α and p, respectively.

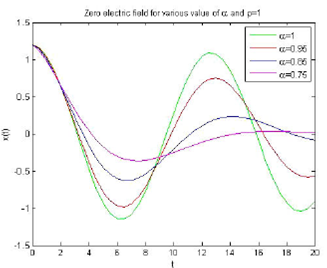
Figure 1 Wave solutions to Eq. (14) for a zero electric field in a plasma for different values of the parameter a. Here, ρ = 1, x₀ = 1:2, and ω = 0:5. 

Figure 2 Wave solutions to Eq. (14) for a zero electric field in a plasma for different values of the parameter ρ. Here, a = 0:95, x₀ = 1:2, and ω = 0:5 

2.2.Static electric fields

Now we apply a static field, E(t) = E₀, with the initial conditions x(0)=x0 (x0>0) and ẋ0=0.

Equation (9) may be written as follows

GCDt2α,ρx(t)+ω2x(t)=Ω, (15)

where

Ω=E0ω24πne. (16)

Applying the p-Laplace transform to Eq. (15) and using x(0) = x₀ and ẋ(0)=0, we obtain

s2αx¯(s)-s2α-1x0+ω2x¯(s)=Ω1s. (17)

Simplifying above equation, we have

x¯(s)=x0s2α-1s2α+ω2+Ωω21s-s2α-1s2α+ω2. (18)

As derived in ¹², Eq. (18) gives

x(t)=x0-Ωω2E2α-ω2tρρ2α+Ωω2. (19)

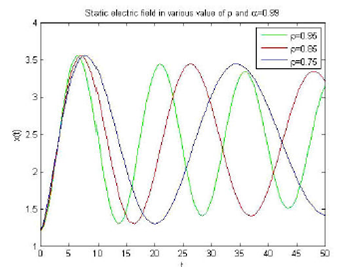
Figures 3 and 4 depicts depict the behavior of wave solutions to Eq. (19) for a static electric field in a plasma for various values of the parameters α and ρ, respectively.

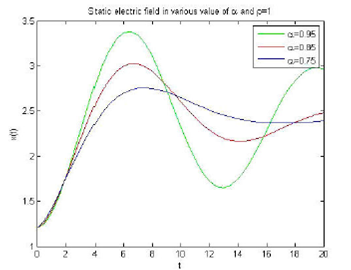
Figure 3 Wave solutions to Eq. (19) for a static electric field in a plasma for different values of the parameter a. Here, ρ = 1, x₀ = 1:2, Ω = 0:6, and ω = 0:5. 

Figure 4 Wave solutions to Eq. (19) for a static electric field in a plasma for different values of the parameter ρ. Here, a = 0:99, x₀ = 1:2, Ω = 0:6, and ω = 0:5. 

3.Fractional modeling of electromagnetic waves in dielectric media

The Maxwell equations in dielectric media ²¹ are

Taking the curl of Eq. (23) and using vector identities, we have

which becomes, after using Eq. (20)

Taking the time derivative of (22) gives

Combining Eqs. (25) and (26), the wave propagation in the x direction is written as

where S(x,t) is the current density source, which may be constant, sinusoidal, or stepped ^16-18. If S(x,t) = 0 then Eq (27). is called a homogeneous wave equation and if S(x,t)≠0 then (27) is called an inhomogeneous wave equation.

In the present case, we are considering unit step source S(x,t) = 1 for x≥0 and S(x,t) = 0 for x < 0 is often the current density source ²⁸.

In order to make the fractional differential equation dimensionally consistent, an alternative procedure for constructing fractional equations was reported in ¹⁹. The proposed alternative is the introduction of an additional parameter α, which must have dimension of seconds or meters(for the temporal or spatial operator, respectively) to be consistent with the dimension of the ordinary operator. To do this, we replace the ordinary time operator by the fractional one as follows,

In the spatial case, we can replace the ordinary operator by the fractional spatial operator as so that

where α_x has dimension of length and α_t has dimension of time. These parameters characterize the fractional spatial or fractional temporal structures (components that show an intermediate behaviour between a system conservative and dissipative), when δ and γ are equal to 1, the expression (28) and (29) reduce to ordinary derivative. Considering (28) and (29), the fractional representation of (27) is

the order of the derivative to be considered is 0<δ,γ≤1 for the fractional wave equation in space-time domain, respectively.

3.1.Fractional space wave equation in dielectric media

In this section, we will investigate the solutions of the fractional space-time wave equation in dielectric media via fractional derivative of constant order with generalised Caputo fractional derivative.

Let us consider Eq.(30) the spatial fractional wave equation with the Caputo generalized fractional derivative is given by

GCDx2α,ρE(x,t)-μϵαx21-α∂2Ex,t∂t2=αx21-αS(x,t) (31)

where S(x,t) = 1 for x≥0 and S(x,t) = 0 for x<0.

Now, assuming its solution

E⃗(x,t)=R(E0⃗eiωtu(x)), (1)

where R is the real part and substituting Eqs.(31) and (32) into (30), we have

GCDx2α,ρ(u(x))+θ^2u(x)=αx2(1-α), (33)

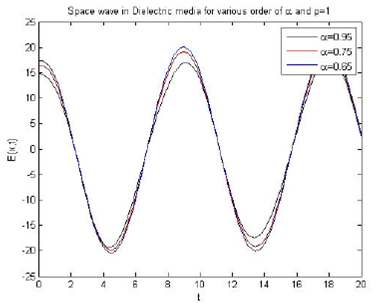
Figure 5 Spatial wave solution for dielectric media fields for different values of the parameter a. Here, ρ = 1, u₀ = 1.2,|θ² = 0:7, a _x = 1:25, and E₀ = 12. 

Figure 6 Spatial wave solution for dielectric media fields for different values of the parameter ρ. Here, a = 0:95, u₀ = 1.2, θ² = 0.7, a _x = 1:25, and E₀ = 12. 

where θ2=μϵω2 is the wave number and θ^2=θ2αx2(1-δ) is the wave number in presence of fractional space components. Equation is often referred to as the fractional Helmholtz equation with generalized Caputo fractional derivative. For this equation, if θ^2 has a negative value, then the behavior of E⃗(x,t) for the space coordinate grows or decays exponentially, but if θ^2 has a positive value, then E⃗(x,t) will vary sinusoidally or cosinusoidally for the space coordinate and varies with time in a simple harmonic motion.

Applying p-Laplace transform to Eq.(33) and considering u(0) = u₀ and u̇(0)=0, yields

s2αu¯(s)-s2α-1u0+θ2u¯(s)=αx2(1-α)s (34)

After simplification, we get

u¯(s)=αx2(1-α)s(s2α+θ^2)+s2α-1u0s2α+θ^2 (35)

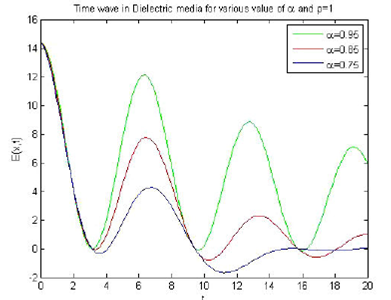
Figure 7 Time wave solution for dielectric media fields for different values of the parameter a. Here, ρ = 1, u₀ = 1.2, ω = 0:5, Ω = -0.06, and E₀ = 12. 

As derived in ¹², Eq. (35) gives

ux=αx2(1-α)1θ^2-1θ^2E2α-θ^2xρρ2α+u0E2α-θ^2xρρ2α. (36)

Therefore we get solution of Eq.(31)

E(x,t)=Reiωtu(x), (37)

where u(x) is given in Eq. (36)

3.2.Fractional time wave equation in dielectric media

Considering the Eq. (30), the temporal fractional wave equation via Caputo generalized fractional derivative is given by

GCDt2α,ρE→x,t-αt21-αμϵ∂2Ex,t∂x2=αt21-αμϵS(x,t) (38)

where S(x,t) = 1 for t≥0 and S(x,t) = 0 for t < 0. Now, assuming the following solution

E⃗(x,t)=R(E⃗0eiωxu(t)), (39)

yields, after substituting into Eq. (30), we have

GCDt2α,ρ(u(t))+ω2u(t)=-Ω2, (40)

where ω2=(k2/μϵ)αt2(1-α)=ω02αt2(1-α) is the fractional relation, ω₀ is natural frequency of the wave and Ω2=(1/μϵ)αt2(1-α) is the velocity of the electromagnetic wave considering fractional components.

Applying p-Laplace transform to Eq.(40) and considering u(0) = u₀ and u̇(0)=0 yields the following expression

u¯(s)=u0s2α-1s2α+ω2-Ω2ss2α+ω2, (41)

As derived in ¹², Eq. (41) gives rise to the following solution to Eq. (38)

E→x,t=Reiωxu0+Ω2ω2×E2α-ω2tρρ2α-Ω2ω2. (42)

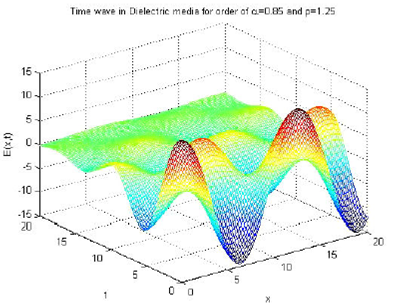
For the time wave solutions within a dielectric medium, a gradual increase in the value of α results in an increase of frequency and a corresponding decrease in wavelength. This effect can be directly observed from Figs. 8 and 9. Similarly, a variation of ρ also results in a frequency increase.

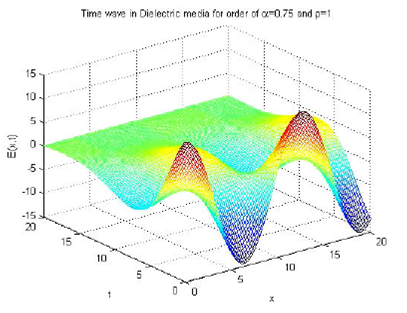
Figure 8 Time wave solution for dielectric media fields. Here,a = 0.75, ρ = 1, u₀ = 1.2, ω = 0.5, Ω = -0.06, and E₀ = 12. 

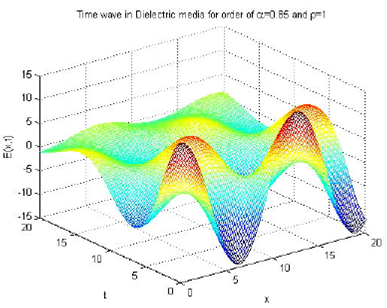
Figure 9 Time wave solution for dielectric media fields. Here, a = 0.85, ρ = 1, u₀ = 1.2, ω = 0.5, Ω = -0.06, and E₀ = 12. 

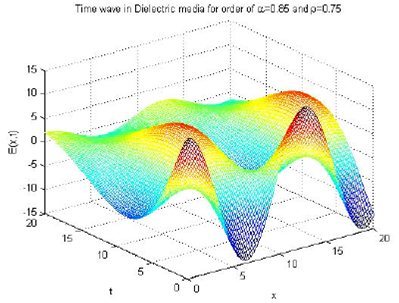
Figure 10 Time wave solution for dielectric media fields. Here, a = 0.85, ρ = 0.75, u₀ = 1.2, ω = 0.5, Ω = -0.06, and E₀ = 12. 

Figure 11 Time wave solution for dielectric media fields. Here, a = 0.85, ρ = 1.25, u₀ = 1.2, ω = 0.5, Ω = -0,06, and E₀ = 12. 

4.Conclusion

In this paper, we have studied the behavior of electromagnetic waves described by a fractional differential equation of order 0<α<1 in the the plasma and dielectric media modelled with Caputo generalized fractional derivatives. With the purpose of maintaining the physical units of the system, the auxiliary parameters α_x and α_t are introduced to characterize the existence of the fractional space and time components, respectively; these parameters show that the system has an intermediate behavior between a conservative and dissipative system. For vanishing and static electric fields, the analytical solutions are given in terms of the Mittag-Leffler function. The p-Laplace transform is used to derive exact solution of models.

The solution of Eqs. (10) and (15) correspond to zero electric field and static electric field using generalized Caputo fractional derivative in a plasma, respectively. From Fig. 1, it was found that a decrease in the value of α implies a wavelength increase; hence, both the frequency and the wave amplitude decrease in the case of vanishing electric field within a plasma. In Fig. 2, we observe a similar behavior where an increase in ρ gives rise to a decrease in both amplitude and wavelength. The solution of zero electric field and static field is obtained in Mittag-Leffler function such as given in Eqs. (14) and (19), respectively. In the case of a static field, Fig. 3 shows that if the value of the parameter α is decreased, the wavelength increases and, consequently, both the frequency and amplitude decrease. Figure 4 depicts a similar effect for an increase in ρ, where wavelength decreases, frequency increases, and the amplitude remains the same.

The solution of Eqs. (31) and (38) correspond to the spatial and time wave equations in a dielectric medium using Caputo generalized fractional derivatives. Figure 5 shows that when we decrease a value of α, both wavelength and frequency remain the same while there is a change in the amplitude for the spatial wave within dielectric media. From Fig. 6, it can be concluded that as the value of ρ decreases, wavelenth increases and both the amplitude and frequency decrease. The solutions for spatial and time waves in dielectric media were also obtained using the Mittag-Leffler funciton as given in (37) and (42), respectively. If θ^2 has a negative value, then the behavior of E⃗(x,t) for the space coordinate grows or decays exponentially, but if θ^2 has a positive value, then E⃗(x,t) will vary sinusoidally or co-sinuosoidally for the space coordinate and varies with time in a simple harmonic motion. In Fig. 7, as α decreases, the wavelength increases and therefore, frequency and amplitude decrease. We can also conclude that as α→0, the wave periodicity disappears as can be seen from the same figure.

The solutions of fractional differential equations with generalized Caputo fractional derivatives display a change within the amplitude of the electric field and variations in the phase exhibit fractality in time to different scales and suggests the existence of heterogeneities within the medium. These behaviors depend on the fractional derivative order of α and ρ. The systems exhibit a quick stabilization than it takes the integer exponent. We showed the electric field waves that are transmitted in the material present anomalous behavior depending of the value of α or ρ in the fractional differential equation. Usually this anomalous behavior is known in the literature as centrovelocity or propagation of energy in dissipative systems .

Further analysis of this article may prove to be helpful for a better understanding of electrical systems, wave propagation, and scattering in radom media.