1. Introduction
There is an increasing appreciation of the importance of low, intermediate, and high energy positron for both scientific and technological applications [1]. Positron offers new ways to study a wide range of other phenomena, including plasmas [1], atomic clusters, and nanoparticles [2]. In the last decade, with the availability of the highly efficient buffer-gas positron accumulation technique and new innovative developments in trap based beams, it is now possible to create cold, bright, low-energy monochromatic positron beam [1], and this serves as a strong motivation for the theorists to extend their studies to explore specifics targets. Most of these studies using positron depend on a quantitative understanding of the basic interactions of positrons with matter [1,2]. Positron scattering is expected to be significantly different from the analogous collisions involving electrons. For example, the repulsive short range positron-target interaction, in contrast to the attractive electron-target interaction, the absence of exchange interaction for positron, and the positronium channel, where a rigorous treatment (especially for many-electron targets) of this process is difficult, and this remains one of the most significant challenges for positron scattering theory [1,2]. We can find only a few scientific publications on electronic excitation of molecules by positron impact, as H2 [36], N2 [7,8], CO [9,10], and CO2 [11]. Most of the work produced was based on classical collision theory, several first principle theories, and with the advance of quantum mechanical computational methods, some very accurate ab initio calculations were performed [12]. Nevertheless, these calculations are very time-consuming, limiting the domain of such models for positron scattering. Late on, the scaling of plane wave Born (or BEf-scaling), which was originally designed to describe electron-molecule collision [13-15], was adapted by Lino [16-18] to describe positron-molecule scattering processes. Comparison with available theoretical calculations and experimental data showed that the method proposed by Lino [16-18], called scaling Born positron (SBP), is very accurate when compared with sophisticate methods (cross sections for positron-H2, N2, and CO have been calculated to illustrate the improved SBP model). Motivated by an earlier theoretical effort, we have investigated the electronic excitation of C6H6 using the SBP approach.
As well known, Benzene (C6H6) is a very important chemical compound due to its role as a precursor in pharmaceutical and petrochemical industries [19]. Considering its importance, it is somewhat surprising that studies investigating electron and positron scattering from C6H6 are not numerous. In 2011, electronic excitation cross sections of C6H6 (1B 1u , and 1E 1u electronic states) molecules by electron impact were obtained by Kato et al, [19], and their experimental results were in reasonable agreement with the preliminary theoretical study [19]. To the best of our knowledge, there are no corresponding theoretical or experimental results for positron-C6H6 scattering. We present a preliminary study on the system e +-C6H6, which provides a possible explanation of similarities and differences in (electron/positron)C6H6 scattering.
In Sec. 2, we identify the SBP method for positron scattering. In Sec. 3, computational procedures and results are discussed. Conclusions are presented in Sec. 4.
2. Theory
A simple and computational fast way to calculate electron (or positron) collisional excitation cross sections for targets in general is the plane-wave Born approximation (or the socalled First Born Approximation-FBA). Consider the prescription for the scattering amplitude given using FBA,
where V is the Coulombic interaction between the incident positron and the molecular target and Φ i and Φ f are initial and final electronic states of the target, respectively. Scattering amplitudes obtained from FBA are valid for high-energy static calculation, and as the FBA cross-section treats the positron as a plane wave, no resonances should be found in the cross-section. When dealing with dipole transitions, the long-range character of the dipolar coupling requires a larger number of partial waves[4] and because of it, higher partial waves are not well described for several sophisticated theoretical methods [4] (to repair this problem, a traditional Born-closure scheme is frequently used in the literature but this procedure represent a great computational effort). Later on, the scaling Born positron (SBP) approach, which was originally designed to describe electron-molecule[13], was adapted by Lino[16] to positron-molecule scattering processes. The scaling Born positron (SBP), σ SBP(E), is given by
where
To analyze the behavior of f(E), we assume that the f(E) term is related to the energy change of the incident positron in the field of the nucleus and the bound electrons of the target. E ps is the positronium energy, E exc is the excitation energy, E is the energy incident, f accur is an accurate dipole value from experiments or accurate wavefunctions, and f Born is the dipole value from FBA (these quantities are accessible from accurate wave functions and hence are free of adjustable parameters and also has the effect of replacing the poor or marginal wavefunctions of the target)[16]. The SBP approach has the effect of correcting the wave function used for FBA without losing its well-known validity at high energy and the SBP approach has been shown to produce atomic and molecules excitation cross sections comparable in accuracy to those obtained by more sophisticated collision theories [16].
3. Computational procedures and results
For the positron-C6H6 scattering system we have used the fixed-nuclei approximation at the experimental D 6h geometry, i.e., r(C-C) = 1.39 A, and r(C-H) = 1.08 A. To define a good Cartesian basis set to produce a scattering calculation is not an easy task; as pointed out by Bettega et. al. [20] there are no clear rules or procedures to construct a trial scattering basis. Because the required number of Gaussian functions to obtain convergence increased substantially with the target, we have used the proposed by Bettega et al. [20]. The basis set, which was originally applied by Bettega et. al. [20] in the elastic electron-C6H6 scattering [20], was here adapted with one d-type uncontracted functions in each hydrogen atom. We have modified the exponents of the diffuse s, and p- type functions. The final exponents chosen are shown in Table I.
TABLE I Exponents of the diffuse s, and d functions used.
| Type | Bettega et al [20] | Present |
| s | 0.06 | 0.055 |
| p | 0.06 | 0.055 |
| d | 1.60 | 1.45 |
The results with these small modifications get very similar ground state energy. The wave functions for the excited electronic states were all generated with the improved virtual orbital (IVO) method (see, Ref. [21]. It has been noted that some symmetries may, in combination with the diffuse s-type Gaussian Cartesian, give rise to linear dependence in the basis set used. Bettega et al.[21] obtained a good description of the target, and they were able to add and adjust Gaussian functions to an adequate convergence [20]. Our study of the target (configuration) covers the calculation generated by Bettega et al. [20] (here one d-function only). If we are not so rigorous, we can see in Table II a reasonable agreement between the results (Table II shows electronic excitation compared with experimental data [22]).
TABLE II Vertical excitation energies for the states of C6H6 molecule in electron volts (eV).
| Molecule (state) | Eexc (eV) | Ref. [22] |
| C6H6 (1B1u) | 6.18 | 6.19 |
| C6H6 (1E1u) | 6.90 | 6.96 |
As well known, resonances in positron-molecule scattering are expected to be rare due to the nature of the positrontarget interaction. Scattering amplitudes obtained from FBA are valid for high-energy static calculations, i.e., in situations where the target wave functions can be considered frozen. Provided good wave functions are employed, the FBA crosssection is nearly the basis set independent. Besides, as FBA treats the positron incident as a plane wave, no resonances should be found in the cross-section. This consideration represent a step very important, i.e., the fully ab initio method used by Bettega et al. [20], called SMC method, is able to perform calculations for electron and also positron-molecule scattering but the method can considerably enlarge the computational effort. This same computational effort is obviously not found in the FBA case. Table III and IV shows our integral cross sections (ICS) using FBA compared with experimental data (electron case) [19].
As observed in Table III and IV, the FBA showed much larger cross sections and this is evidently expected. To test Eq. (3), we have used the threshold energy for positronium formation
TABLE III ICS (10-16cm2) for the 1B1u electronic state using FBA.
| E(eV) | FBA(present work) | Experiment (electron)[19] |
| 7.0 | 0.649 | |
| 10 | 1.397 | |
| 20 | 1.718 | |
| 30 | 1.575 | |
| 40 | 1.417 | |
| 50 | 1.281 | |
| 60 | 1.170 | |
| 70 | 1.077 | |
| 80 | 0.999 | |
| 90 | 0.933 | |
| 100 | 0.875 | 0.279 |
| 200 | 0.560 | 0.199 |
| 300 | 0.422 | |
| 400 | 0.342 | |
| 500 | 0.288 | |
| 600 | 0.248 |
TABLE IV ICS (10−16cm2) for the 1E1u electronic state using FBA.
| E(eV) | FBA(present work) | Experiment (electron)[19] |
| 10 | 7.342 | |
| 20 | 11.651 | |
| 30 | 11.273 | |
| 40 | 10.412 | |
| 50 | 9.565 | |
| 60 | 8.820 | |
| 70 | 8.179 | |
| 80 | 7.633 | |
| 90 | 7.161 | |
| 100 | 6.743 | 1.812 |
| 200 | 4.397 | 1.269 |
| 300 | 3.341 | |
| 400 | 2.721 | |
| 500 | 2.325 | |
| 600 | 2.054 |
where 6.8 eV represents the ground state binding energy of positronium and “B” ionization energy of the target. A rigorous treatment of this process (positronium) is difficult, especially for many-electron targets (as cited before, this remains one of the most significant challenges for positron scattering theory). The f acc, and f Born value deduced from the OOS by Kato et al [19] was used in the present study. Table V shows f acc(f Born) values used by Kato et al. [19].
Figure 1 shows integral cross-sections (ICS) for C6H6 (1B 1u , state) using the SBP approach. As mentioned before no experimental data or theoretical studies are reported in the literature for this system. The SBP cross sections are compared with results of Kato et al, [19] for electron scattering. Kato et al, [19], in conjunction with experimental technique, have used a full description of the BEf-scaling approach for electron scattering. It is important to mentioned that polarization effects are not considered in the present study. Note that, at lower energies, the corresponding excitation cross sections by electron impact is similar but smaller. As observed also in the high energy region, for the static potential interaction the first Born approximation (FBA) predicts equal cross-sections for positrons and electrons and this convergence between BEf-scaling (electron) and SBP approach can be observed in Fig. 1 at high energies. This consideration is imperative, i.e, the convergence of the cross-sections (electron and positron) for heavier molecules represents an open question in the literature [22] and the present result suggests that the SBP approach may permit an efficient and reliable tool for study convergence between the cross sections. These results suggest that the SBP approach is consistent, and evidently, we kindly suggest a future experimental verification of the positron scattering cross section for this electronic excitation.
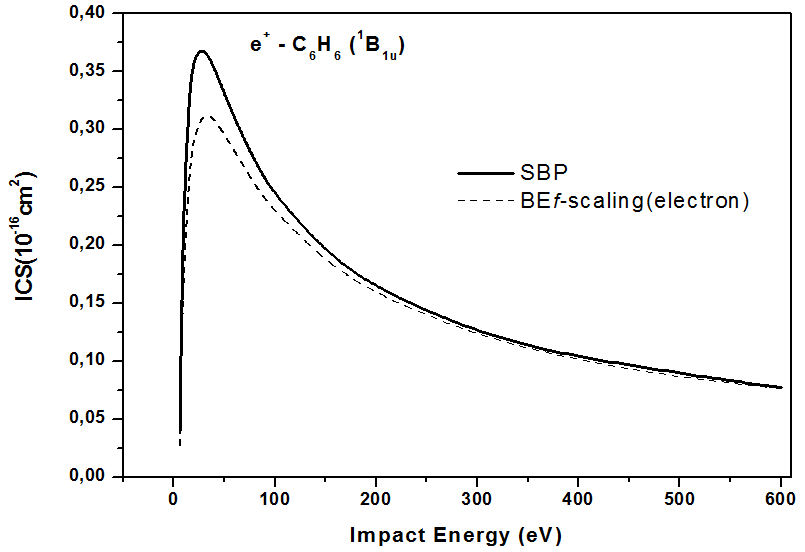
FIGURE 1 Integral cross sections (10−16 cm2) for positron impact excitation of 1B 1u electronic state in C6H6. Solid line, our SBP approach; dashed line, BEf-scaling (electron) [19].
Figure 2 shows integral cross-sections for C6H6 (1E1u, state) using the SBP approach. As Fig. 1, no cross-sections in the literature are reported for this transition; and again, our results are compared with electrons scattering observed by Kato et al. [19] (the error experimental on the integral crosssection is ∼23%). Again similar behavior (sharp) is found for the 1E1u excitation process when compared with electron scattering. As noted at higher energies where the static potential dominates, the scattering process the integral crosssections for electron and positron tend to get closer. We also provide integral cross sections in Table VI for future reference.
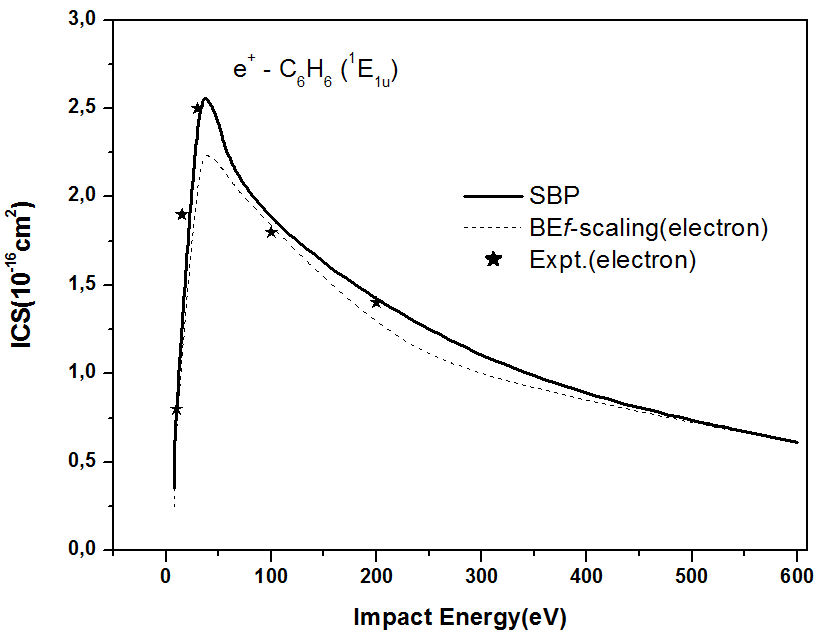
FIGURA 2 Integral cross sections (10−16 cm2) for positron impact excitation of 1E 1u electronic state in C6H6. Solid line, our SBP approach; dashed line, BEf-scasling (electron) [19]; star black, experimental data (electron) [19].
TABLE VI Integral cross sections (10−16cm2) for e+-C6H6 scattering (1B1u , and 1E1u electronic states) using SBP approach.
| E (eV) | SBP(1E1u) | SBP(1B1u) |
| 7.5 | 0.350 | 0.119 |
| 8.0 | 0.542 | 0.146 |
| 8.5 | 0.713 | 0.170 |
| 9.0 | 0.871 | 0.191 |
| 10.0 | 1.150 | 0.228 |
| 15.0 | 2.025 | 0.329 |
| 20.0 | 2.405 | 0.364 |
| 30.0 | 2.605 | 0.371 |
| 40.0 | 2.556 | 0.353 |
| 50.0 | 2.440 | 0.331 |
| 60.0 | 2.311 | 0.310 |
| 70.0 | 2.187 | 0.290 |
| 80.0 | 2.071 | 0.273 |
| 90.0 | 1.949 | 0.258 |
| 100 | 1.869 | 0.244 |
| 200 | 1.272 | 0.162 |
| 300 | 0.980 | 0.124 |
| 400 | 0.810 | 0.102 |
| 500 | 0.693 | 0.098 |
| 600 | 0.613 | 0.077 |
4. Conclusions
The results presented in this paper demonstrate the utility of the SBP approach to calculating integral cross-sections (ICS) using positron as an incident particle. The SBP approach can be used to predict cross-sections, because the values of E exc and E ps are either available in the literature, or can be calculated from high-quality wave functions. The SBP approach used in this paper should not diminish the value of more sophisticated methods that produce highly accurate results, though they require orders of magnitude more computational effort than SBP cross-sections and where such calculations are impractical or unavailable at this time, we believe the SBP approach procedure does offer a very useful alternative. We suggest a future experimental verification for e + C6H6 scattering in order to stimulate theoretical work.











 nueva página del texto (beta)
nueva página del texto (beta)


