1. Introduction
The interactions of quantum systems with the spherically symmetric potentials have been studied by researchers since the discovery of quantum mechanics [1-3]. From the early days of quantum mechanics, the study of exactly solvable problems has attracted a considerable attention in many areas of physics, particularly in atomic physics, information theory, nuclear physics, particle physics, molecular physics and its importance cannot be overemphasized [4,5]. The exact solution of the relativistic and non-relativistic equations for most of these types of potentials is not attainable and approximations become indispensable [6]. For instance, in the case of the Schrödinger equation, when the angular momentum quantum number is present, one can resort to solve the non-relativistic equation approximately via a suitable approximation scheme [7]. Some of such approximations, yielding good results, consist of the conventional approximation scheme proposed by Greene and Aldrich [8], the improved approximation scheme by Jia et al. [9], the elegant approximation scheme [10], the Pekeris approximation [11], the improved approximation scheme by Yazarloo et al. [12], improved approximation scheme in Refs. [13-15] and in Refs. [16,17].
Over the past decades, problems involving the multidimensional Schrödinger equation have been addressed by many researchers using different analytical procedures. For examples, Ntibi et al. [18] investigated the analytical solution of the D-Dimensional radial Schrödinger equation with Yukawa potential. Oyewumi et al. [19] studied the N-dimensional Pseudoharmonic oscillator. Gönül and Koc¸ak [20] investigated explicit solutions for N-dimensional Schrödinger equations with position-dependent mass. The N-dimensional Kratzer-Fues potential was discussed by Oyewumi [21], Ikhdair and Sever [22], studied the modified Kratzer-Fues potential plus the ring shape potential in D-dimensions while Dong [23], reviewed the wave equations in higher dimensions.
The Varshni potential is greatly important with applications, cutting across nuclear physics, particle physics and molecular physics. The Varshni potential model takes the form [24,25]:
where η 0 and η 1 are potential strength parameters, δ is the screening parameter and r the inter-nuclear separation. The Varshni potential is a short-range repulsive potential energy.
The Hulthén potential is one of the important short-range potentials in physics. Its relevance to diverse areas of physics including nuclear and particle physics, atomic physics, molecular physics, condensed matter and chemical physics has been of great interest and concern to researchers in recent times [26,27]. The Hulthén potential model takes the form [28]
where δ is the screening parameter and η 2 is the potential strength constant which is sometimes identified with the atomic number when the potential is used for atomic phenomena. Many authors have obtained bound state solutions of SE with this potential. For example, Tazimi and Ghasempour [29] used the Nikiforov Uvarov (UN) method to obtain bound state solutions of the three-Dimensional Klein-Gordon equation for two model potentials. Quantization rule was employed by Ikhdair and Abu-Hasna [30] to obtain the solution to the Hulthén potential in arbitrary dimension with a new approximate scheme for the centrifugal term. Okorie et al. [31] obtain the solution of Schrödinger equation (SE) with energydependent screened Coulomb potential with the new form of Greene-Aldrich approximation using the NU method.
With the experimental proof of the Schrödinger wave equation, researchers have made great effort to solve the SE by the combination of two or more potentials, which can be used for a wider range of applications [32]. For example, Edet et al. [33] obtained bound state solutions of the SE for the modified Kratzer potential plus screened Coulomb potential including a centrifugal term. Also, Edet et al. [34] obtained any-state solutions of the SE interacting with Hellmann-Kratzer potential model. William et al. [35] obtained bound state solutions of the radial SE by the combination of Hulthén and Hellmann potential within the frame-work of Nikiforov-Uvarov (NU) method for any arbitrarystate, with the Greene-Aldrish approximation in the centrifugal term. Inyang et al. [36] studied any-state solutions of the SE interacting with class of Yukawa-Eckart potentials within the framework of NU method. Hence, motivated by the success of the combination of exponential-type potentials, we seek to investigate the bound state solutions of the SE by the combination of Varshni potential, of Eq. (1), and the Hulthén potential of Eq. (2) using the NU method. The resulting potential, so-called the Varshni-Hulthén potential (VHP), takes the form
Considering the achievements in the previous studies, we combine the potentials to allow for more physical application and comparative analysis to existing studies of molecular physics. Also in molecular physics, it is well-known that the potential energy functions with more parameters have a tendency to fit experimental data better than those with fewer parameters [37]. The plot of the combined potential for different values of the screening parameter δ is presented in Fig. 1.
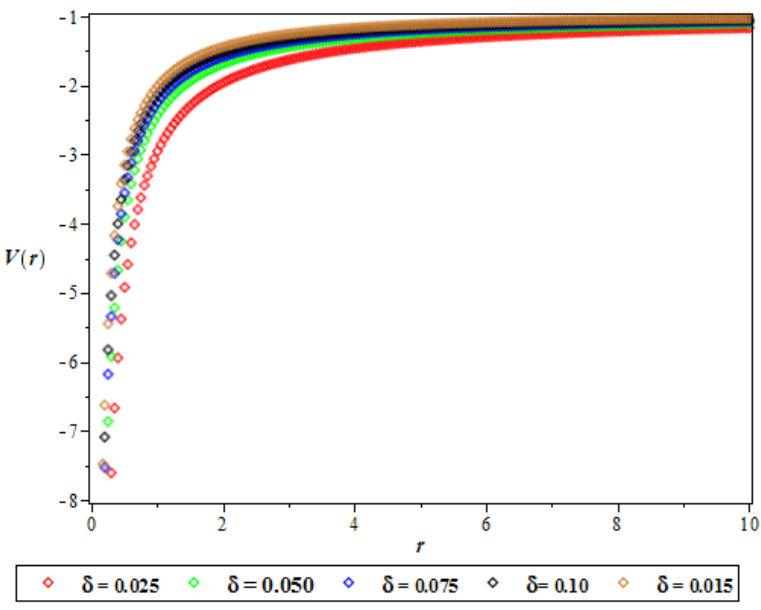
FIGURE 1 Plot of the combined potential as a function of internuclear distance for different screening parameter. We choose η 0 = η 1 = −1, and η 2 = 0.025.
However, it must be noted that the exact solution of the SE with the combined potentials in Eq. (3) is not possible due to the presence of the centrifugal term. Therefore, to obtain approximate solutions, we employ a suitable approximation scheme. It is found that such approximation proposed by Greene and Aldrich [8],
is a good approximation to the centrifugal or inverse square term for a short range potential which is valid for δࠏ1.
The paper is organized as follows: In Sec. 2, we derive the bound state solutions of the SE with VHP using NU method and also derive the corresponding normalized wave function. In Sec. 3, we present the results and discussion and finally, we make a concluding remark in Sec. 4.
2. Bound state solutions of the Schrödinger equation with Varshni plus Hulthén potentials
In this study, we adopt the Nikiforov-Uvarov method which is based on solving the second-order differential equation of the hypergeometric type. The details can be found in Ref. [38]. The SE takes the form Ref. [39]
where l, µ, r, N,
and
By using coordinate transformation
we obtain the differential equation as
where
Now that Eq. (8) and Eq. (1) of Ref. [38] are in the same shape, we have the following parameters:
Substituting Eq. (10) into Eq. (11) of Ref. [37], we obtain π(x) as
where
To find the constant k, the discriminant of the expression under the square root of Eq. (11) must be equal to zero. As such we have that
Substituting Eq. (13) into Eq. (11) yields π(x) as
and τ(x) can be written as
Taking the derivative of Eq. (15) with respect to x, we have
Referring to Eq. (10) of Ref. [38], we define the constant γ as,
and taking the derivative of σ(x) with respect to x from Eq. (10), we have
Substituting Eqs. (15) and (18) into Eq. (13) of Ref. [38], we obtain
By comparing Eqs. (17) and (19), using Eq. (9) yields the energy eigenvalues equation of the VHP as a function of n and l as
where
To obtain the corresponding wavefunction, we consider Eq. (3) of Ref. [38], and upon substituting Eqs. (10) and (14) and integrating, we get
To get the hypergeometric function, we first determine the weight function ρ(x). By substituting Eqs. (10) and (14) into Eq. (3) of Ref. [38] and after integrating, we obtain
Hence, by substituting Eqs. (10) and (23) into Eq. (2) yields the Rodrigues equation given as
where N nl is the normalization constant. Equation (24) is equivalent to
where
Using the normalization condition, we obtain the normalization constant as follows:
From our coordinate transformation of Eq. (7), we have that
By letting, y = 1 − 2x, we have
Let
and
By substituting Eq. (29) into Eq. (28), using Eq. (30), we have
According to Onate and Ojonubah [40], integral of the form in Eq. (31) can be expressed as
Hence, by comparing Eq. (31) with the standard integral of Eq. (32), we obtain the normalization constant as
3. Discussion
Solution of the radial N-dimensional SE for the newly proposed potential obtained by
the superposition of Varshni and Hulthén potentials otherwise known as
Varshni-Hulthén potential are obtain within the framework of NU method by
approximation to the centrifugal barrier. In Table
I, we reported the numerical energy eigenvalues (eV) with
TABLE I Energy eigenvalues (eV) of the Varshni-Hulthen potential for
η0 = η1 =
−1, η2 = 0.025 with
| State | δ | N = 3 | N = 4 | N = 5 |
| 1s | 0.025 | -1.975781250 | -1.419947195 | -1.224992578 |
| 0.050 | -1.526875000 | -1.213252345 | -1.101834379 | |
| 0.075 | -1.397725694 | -1.148269303 | -1.057252171 | |
| 0.100 | -1.333125000 | -1.111565340 | -1.027444000 | |
| 0.150 | -1.262152778 | -1.062800124 | -0.9783441671 | |
| 2s | 0.025 | -1.226250000 | -1.136131084 | -1.086889280 |
| 0.050 | -1.106875000 | -1.055772344 | -1.026860418 | |
| 0.075 | -1.068611111 | -1.027534543 | -1.002633126 | |
| 0.100 | -1.047656250 | -1.010587522 | -0.9858640000 | |
| 0.150 | -1.023819444 | -0.9889295445 | -0.9597536576 | |
| 3s | 0.025 | -1.088142361 | -1.058702155 | -1.039373438 |
| 0.050 | -1.031875000 | -1.015446221 | -1.003900782 | |
| 0.075 | -1.013913966 | -1.001158640 | 0.9908992733 | |
| 0.100 | -1.005902778 | -0.9950120013 | -.09844360000 | |
| 0.150 | -1.004683642 | -0.9961284666 | -0.9827782293 | |
| 3p | 0.025 | -1.086889280 | -1.056823915 | -1.036870313 |
| 0.050 | -1.026860418 | -1.007932642 | -0.9938898525 | |
| 0.075 | -1.002633126 | -0.9842622719 | -0.9683923310 | |
| 0.100 | -0.9858640000 | -0.9650092156 | -0.9444802500 | |
| 0.150 | -0.9597536576 | -0.9289088370 | -0.8933044371 | |
| 3d | 0.025 | -1.084383117 | -1.053693514 | -1.033115626 |
| 0.050 | -1.016831266 | -0.9954100212 | -0.9788734727 | |
| 0.075 | -0.9800715659 | -0.9561018046 | -0.9346320845 | |
| 0.100 | -0.9457871111 | -0.9150053890 | -0.8845475625 | |
| 0.150 | -0.8699012826 | -0.8168854194 | -0.7591039275 | |
| 4s | 0.025 | -1.040625000 | -0.8168854194 | -1.018280391 |
| 0.050 | -1.008906250 | -1.002307899 | -0.9968737506 | |
| 0.075 | -1.002152778 | -0.9980821361 | -0.9935681755 | |
| 0.100 | -1.004414062 | -1.002429482 | -0.9981750400 | |
| 0.150 | -1.027517361 | -1.030202097 | -1.025835317 | |
| 4p | 0.025 | -1.039373438 | -1.025825868 | -1.015778672 |
| 0.050 | -1.003900782 | -0.9948033881 | -0.9868712556 | |
| 0.075 | -0.9908992733 | -0.9812129600 | -0.9710865137 | |
| 0.100 | -0.9844360000 | -0.9724870563 | -0.9582753600 | |
| 0.150 | -0.9827782293 | -0.9631717038 | -0.9365364617 |
TABLE II Energy eigenvalues (eV) of the Varshni-Hulthen potential for
N = 3 with
| State | δ | η0 = −1, η1 = −2, η2 = 0.050 | η0 = −2, η1 = −1, η2 = 0.075 | η0 = η1 = −2, η2 = 0.10 |
| 1s | 0.025 | -4.951406250 | -8.189531250 | -17.90265625 |
| 0.050 | -3.178125000 | -4.979375000 | -10.85562500 | |
| 0.075 | -2.682934026 | -4.144531249 | -8.920017362 | |
| 0.100 | -2.445000000 | -3.763125000 | -8.012500000 | |
| 0.150 | -2.199236110 | -3.391874999 | -7.115069440 | |
| 2s | 0.025 | -1.951875000 | -3.502500000 | -5.903125000 |
| 0.050 | -1.492500000 | -2.684375000 | -4.107500000 | |
| 0.075 | -1.353819444 | -2.461250000 | -3.590902778 | |
| 0.100 | -1.280625000 | -2.352656250 | -3.332500000 | |
| 0.150 | -1.195277778 | -2.236875000 | -3.048611110 | |
| 2p | 0.025 | -1.950609766 | -3.501230860 | -5.901844140 |
| 0.050 | -1.487412504 | -2.679271879 | -4.102318752 | |
| 0.075 | -1.342319880 | -2.449715279 | -3.579121962 | |
| 0.100 | -1.260100250 | -2.332069000 | -3.311350250 | |
| 0.150 | -1.148818125 | -2.190274722 | -3.000182708 | |
| 3s | 0.025 | -1.397100694 | -2.635225694 | -3.681684028 |
| 0.050 | -1.183125000 | -2.262152778 | -2.860625000 | |
| 0.075 | -1.113937114 | -2.155781250 | -2.610279707 | |
| 0.100 | -1.076111111 | -2.102569444 | -2.476944444 | |
| 0.150 | -1.034359568 | -2.047986111 | -2.320563272 | |
| 3p | 0.025 | -1.395844140 | -2.633967404 | -3.680420530 |
| 0.050 | -1.178089585 | -2.257110418 | -2.855547918 | |
| 0.075 | -1.102593775 | -2.144422285 | -2.598811367 | |
| 0.100 | -1.055933444 | -2.082364000 | -2.456489000 | |
| 0.150 | -0.9889920835 | -2.002556127 | -2.274320787 | |
| 3d | 0.025 | -1.393331033 | -2.631450825 | -3.677893532 |
| 0.050 | -1.168018766 | -2.247025710 | -2.845393765 | |
| 0.075 | -1.079907212 | -2.121704475 | -2.575874807 | |
| 0.100 | -1.015578778 | -2.041953778 | -2.415578778 | |
| 0.150 | -0.8982647085 | -1.911703752 | -2.181843412 | |
| 4s | 0.025 | -1.203750000 | -2.332500000 | -2.905000000 |
| 0.050 | -1.078125000 | -2.117656250 | -2.427500000 | |
| 0.075 | -1.037361111 | -2.056250000 | -2.274444444 | |
| 0.100 | -1.017656250 | -2.028164062 | -2.190625000 | |
| 0.150 | -1.007569444 | -2.011406250 | -2.095277778 | |
| 4p | 0.025 | -1.202496484 | -2.331245508 | -2.903742578 |
| 0.050 | -1.073107813 | -2.112635157 | -2.422459376 | |
| 0.075 | -1.026072450 | -2.044952550 | -2.263085471 | |
| 0.100 | -0.9976000625 | -2.008092250 | -2.170412562 | |
| 0.150 | -0.9625842189 | -1.966385868 | -2.049800365 |
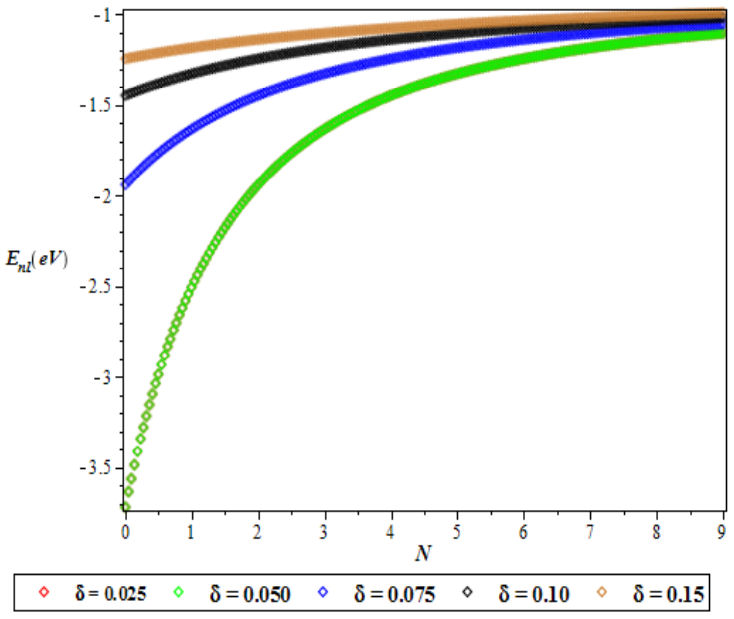
FIGURE 2 Variation of energy eigenvalues as function of N for different l and δ. We choose a = b = −1, and c = 0.025
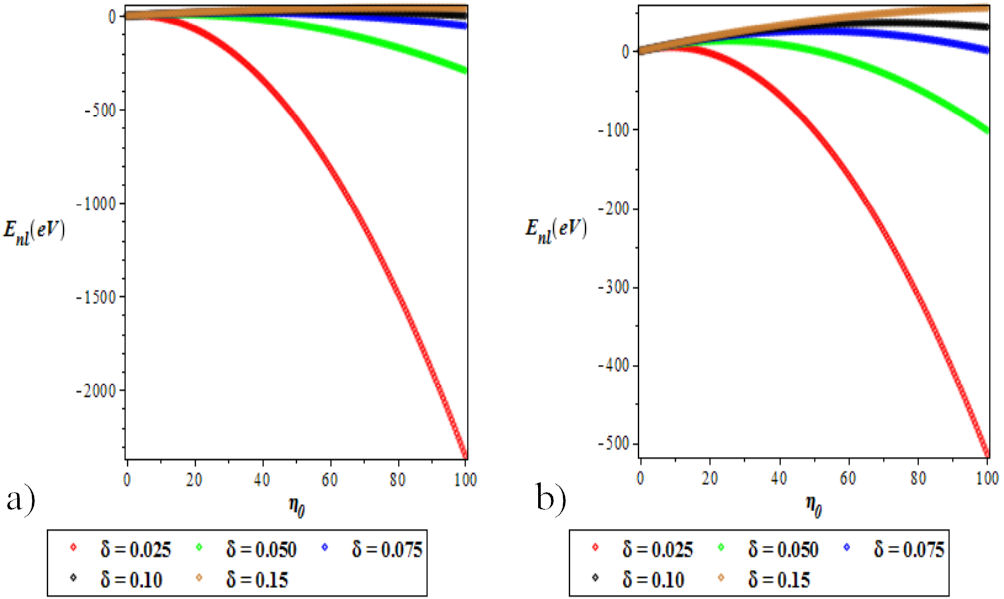
FIGURE 3 a) The plot of the ground state energy spectra for various l as a function of η 0. b) Variation of the first excited state energy spectra for different l as a function of η 0. We choose a = b = −1, c = 0.025 and δ = 0.025 for the ground and excited states.
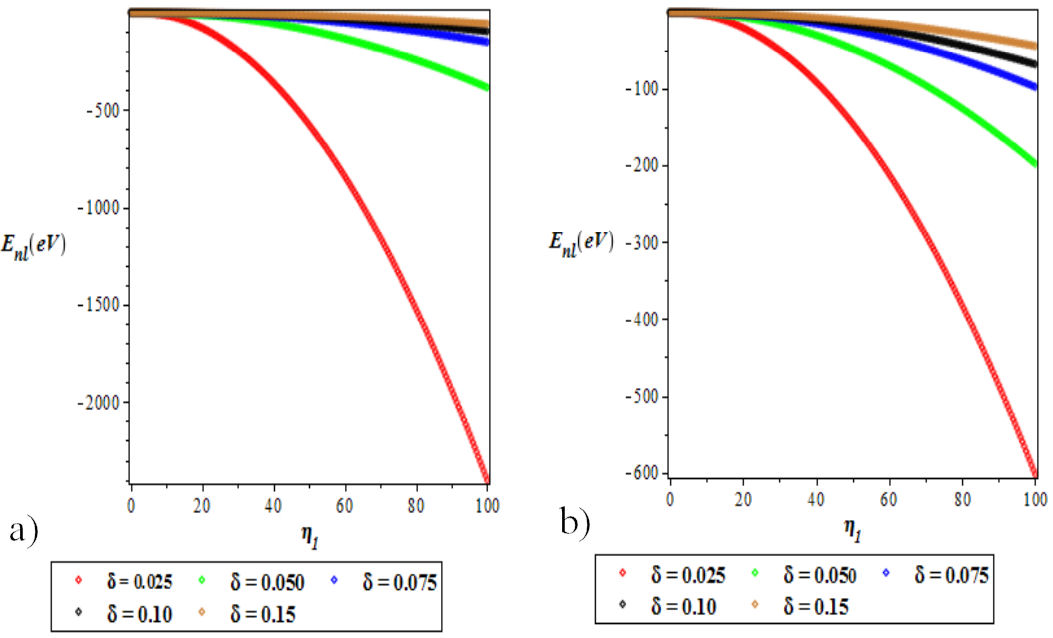
FIGURE 4 a) Variation of the ground state energy spectra for various l as a function of η 1. b) A plot of the first excited state energy spectra for various l as a function of η 1. We choose a = b = −1, c = 0.025 and δ = 0.025 for the ground and excited states.
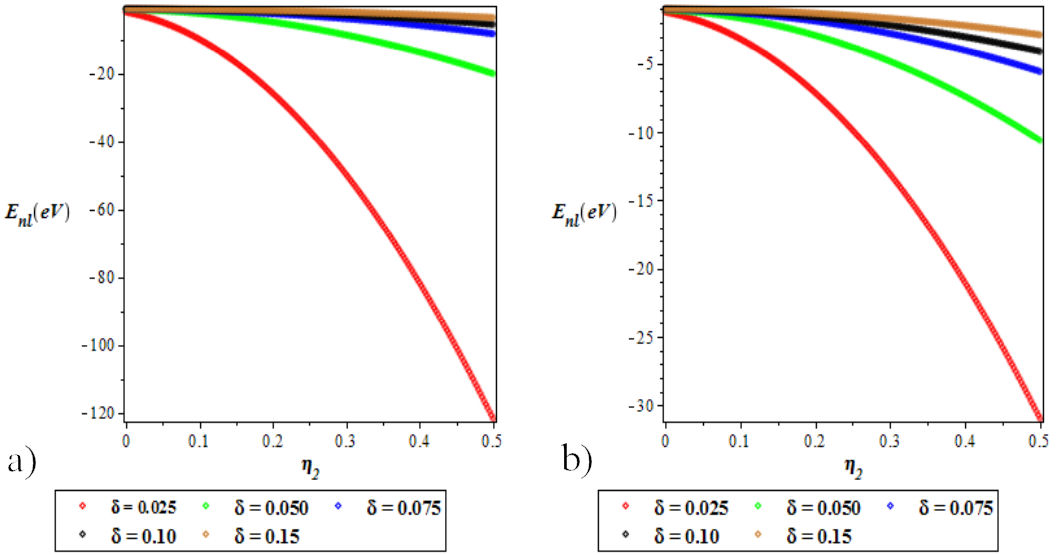
FIGURE 5 a) Variation of the ground state energy spectra for various l as a function of η 2. b) The plot of the first excited state energy spectra for various l as a function of η 2. We choose a = b = −1, c = 0.025 and δ = 0.025 for the ground and excited states.
The variation of energy eigenvalues of VHP as a function of the screening parameter is as shown in Fig. 6a) and 6b). We observed that the energy increases as the screening parameter increases in the ground and excited states. In Fig. 7a) and 7b), we show the variation of energy eigenvalues as a as a function of the reduced mass. It is observed that there is a decrease in the ground and excited states energy for different quantum states as the reduced mass, µ increases.
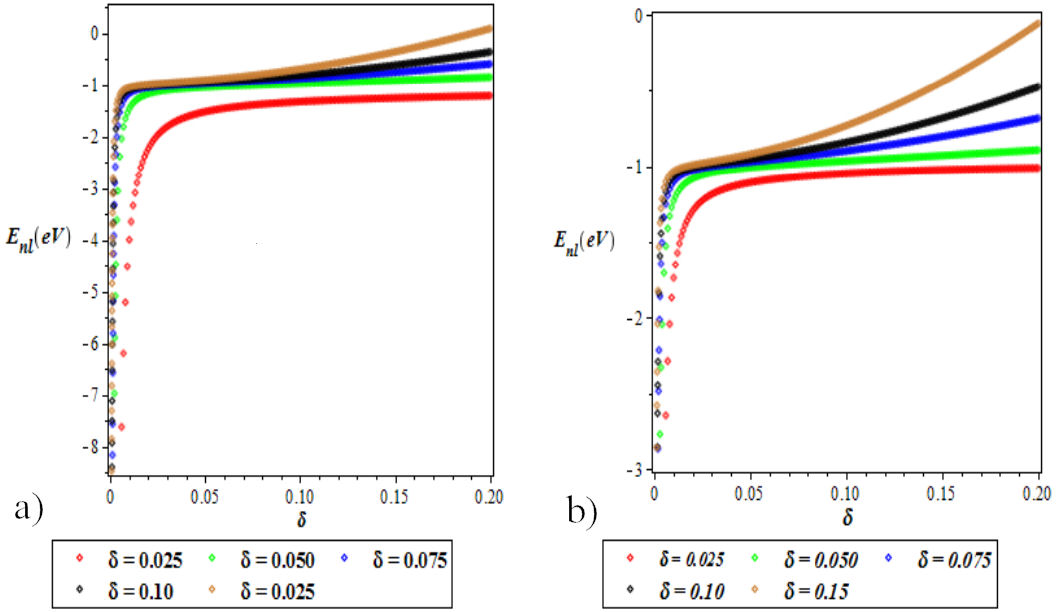
FIGURE 6 a) Variation of the ground state energy spectrum for various l as a function of the screening parameter (δ). b) A plot of the first excited state energy spectrum for different l as a function of the screening parameter (δ). We choose a = b = −1, c = 0.025, and δ = 0.025 for the ground and excited states.
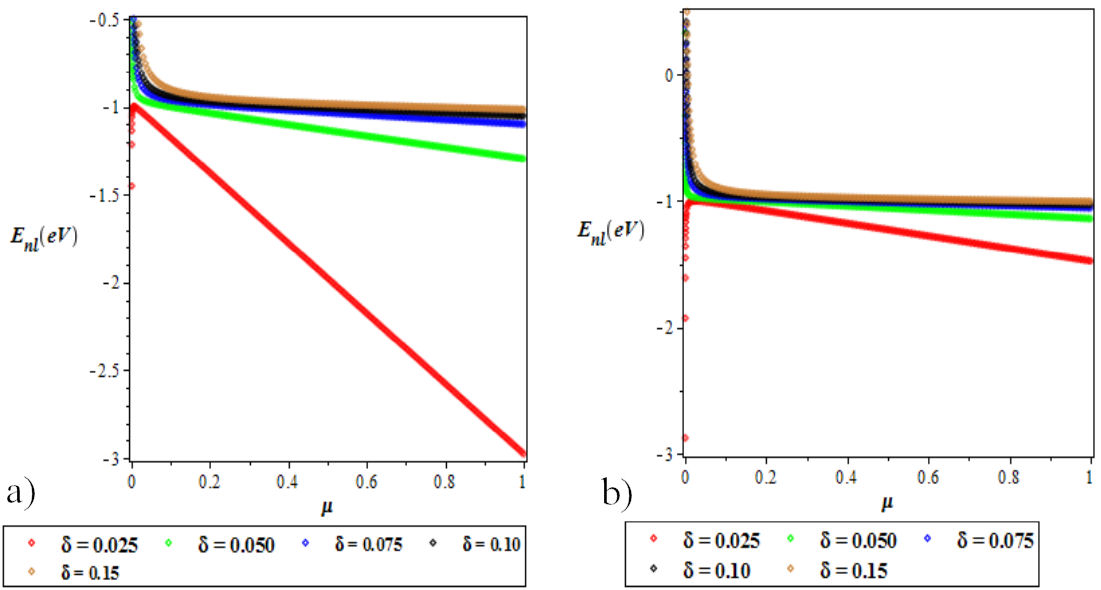
FIGURE 7 a) Variation of the ground state energy spectra for various l as a function of the reduced mass (µ). b). The plot of the first excited state energy spectra for different l as a function of the reduced mass (µ). We choose a = b = −1, c = 0.025, and δ = 0.025 for the ground and excited states.
Special cases
1. When we set η 2 = 0 in Eq. (20), we obtain the energy eigenvalues for the Varshni potential,
where
The numerical energy eigenvalues of Eqs. (34) and (35) for as presented in Table III, were computed for three different potential strengths; for 1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d and 4f states and were found to be in conformity when compared with the work of Ebonwonyi et al. [41] using formula method.
TABLE III Energy eigenvalues (eV) of Varshni potential as a function of the
screening parameter (δ) for in atomic mass units (
| State | δ | Present method a = b = −1 | Present method a = −1, b = −2 | Present method a = −2; b = −1 | (FM) [40] a = b = −1 |
| 1s | 0.001 | -1.063124562 | -2.001000250 | -3.001000250 | |
| 0.050 | -1.092656250 | -2.050625000 | -3.050625000 | ||
| 0.100 | -1.120625000 | -2.102500000 | -3.102500000 | ||
| 2s | 0.001 | -1.063001000 | -1.251001000 | -2.251001000 | |
| 0.050 | -1.090000000 | -1.302500000 | -2.302500000 | ||
| 0.100 | -1.122500000 | -1.360000000 | -2.360000000 | ||
| 2p | 0.001 | -1.063124562 | -1.251249562 | -2.251249562 | -1.0617502 |
| 0.050 | -1.092656250 | -1.311406250 | -2.311406250 | -1.0617502 | |
| 0.100 | -1.120625000 | -1.370625000 | -2.370625000 | -0.9900000 | |
| 3s | 0.001 | -1.028280028 | -1.112113361 | -2.112113361 | |
| 0.050 | -1.058402778 | -1.166736111 | -2.166736111 | ||
| 0.100 | -1.100277778 | -1.233611111 | -2.233611111 | ||
| 3p | 0.001 | -1.028334111 | -1.112223000 | -2.112223000 | |
| 0.050 | -1.057500000 | -1.168611111 | -2.168611111 | ||
| 0.100 | -1.091111111 | -1.230000000 | -2.230000000 | - | |
| 3d | 0.001 | -1.028386250 | -1.112330694 | -2.112330694 | -1.0269447 |
| 0.050 | -1.051736111 | -1.165625000 | -2.165625000 | -0.9867361 | |
| 0.100 | -1.062500000 | -1.206944444 | -2.206944444 | -0.9469444 | |
| 4s | 0.001 | -1.016129000 | -1.063504000 | -2.063504000 | - |
| 0.050 | -1.050625000 | -1.122500000 | -2.122500000 | - | |
| 0.100 | -1.105625000 | -12025000000 | -2.202500000 | - | |
| 4p | 0.001 | -1.016158766 | -1.063565016 | -2.063565016 | -1.0150656 |
| 0.050 | -1.048476562 | -1.121914062 | -2.121914062 | -09951563 | |
| 0.100 | -1.093906250 | -1.193906250 | -2.193906250 | -0.990000 | |
| 4d | 0.001 | -1.028386250 | -1.063624062 | -2.063624063 | -1.0149391 |
| 0.050 | -1.051736111 | -1.116406250 | -2.116406250 | -0.99851563 | |
| 0.100 | -1.062500000 | -1.063624062 | -2.165625000 | -0.9625000 | |
| 4f | 0.001 | -1.016212391 | -1.063681141 | -2.063681141 | -1.0147502 |
| 0.050 | -1.029414062 | -1.1059765662 | -2.1059765662 | -0.9725000 | |
| 0.100 | -1.011406250 | -1.117656250 | -2.117656250 | -0.9306250 |
2. If we set η 0 = η 1 = 0 in Eq. (20), we obtain the energy eigenvalue equation for Hulthén potential
where
The numerical energy eigenvalues of Hulthén potential presented in Eqs. (36) and (37) for N = 3 were computed for 2p, 3p, 3d, 4p, 4d and 4f states and was compare with the work of Qiang et al. [42] using EQR, Bayrak et al. [43] using AIM, and Ikhdair [44] using numerical methods and were found to be in excellent agreement, as presented in Table IV.
TABLE IV Energy eigenvalues (eV) of the Varshni-Hulthen potential for
N = 3 with
| State | δ | Present method | EQR [42] | AIM[43] | Numerical [44] |
| 2p | 0.025 | -0.1127611 | -0.1128125 | -0.1128125 | -0.112760 |
| 0.050 | -0.1010442 | -0.1012500 | -0.1012500 | -0.101042 | |
| 0.075 | -0.0898495 | -0.0903125 | -0.0903125 | -0.089847 | |
| 0.100 | -0.0791769 | -0.0800000 | -0.0800000 | -0.079179 | |
| 0.150 | -0.0593981 | -0.0612500 | -0.0612500 | -0.059441 | |
| 3p | 0.025 | -0.0437072 | -0.0437590 | -0.0437590 | -0.043706 |
| 0.050 | - 0.0331623 | - 0.0333681 | - 0.033368 | - 0.033164 | |
| 0.075 | - 0.0239207 | - 0.0243837 | - 0.0243837 | - 0.023939 | |
| 0.100 | - 0.0159825 | - 0.0168056 | - 0.0168056 | - 0.016053 | |
| 0.150 | - 0.0040162 | - 0.0058681 | - 0.0058681 | - 0.004466 | |
| 3d | 0.025 | - 0.0436044 | - 0.0437587 | - 0.0437587 | - 0.043603 |
| 0.050 | - 0.0327508 | - 0.0333681 | - 0.0333681 | - 0.032753 | |
| 0.075 | - 0.0229948 | - 0.0243837 | - 0.0243837 | - 0.023030 | |
| 0.100 | - 0.0143364 | - 0.0168055 | - 0.0168055 | - 0.014484 | |
| 0.150 | - 0.0003124 | - 0.0058681 | - 0.0058681 | - 0.001396 | |
| 4p | 0.025 | - 0.0199486 | - 0.0200000 | - 0.0200000 | - 0.019948 |
| 0.050 | - 0.0110442 | - 0.0112500 | - 0.0112500 | - 0.011058 | |
| 0.075 | - 0.0045370 | - 0.0050000 | - 0.0050000 | - 0.004621 | |
| 0.100 | - 0.0004269 | - 0.0012500 | - 0.0012500 | - 0.000755 | |
| 4d | 0.025 | - 0.0198457 | - 0.0200000 | - 0.0200000 | - 0.019846 |
| 0.050 | - 0.0106327 | - 0.0112500 | - 0.0112500 | - 0.010667 | |
| 0.075 | - 0.0036111 | - 0.0050000 | - 0.0050000 | - 0.003834 | |
| 4f | 0.025 | - 0.0196914 | - 0.0200000 | - 0.0200000 | - 0.019691 |
| 0.050 | - 0.0100154 | - 0.0112500 | - 0.0112500 | - 0.010062 | |
| 0.075 | - 0.0022222 | - 0.0050000 | - 0.0050000 | - 0.002556 |
3. If we set N = l = 0 in Eq. (20), we obtain the energy eigenvalue equation for the s-wave of VHP as
4. Conclusion
The analytical solutions of the N-dimensional Schrödinger equation for the newly proposed Varshni-Hulthén potential are obtained via NU method by using Greene-Aldrich approximation scheme to the centrifugal barrier. The numerical energy eigenvalues and the corresponding normalized eigenfunctions are obtained for various values of orbital angular momentum quantum number and space dimension. We have also obtained the numerical energy eigenvalues for two special cases of the newly proposed potential and their results were found to be in agreement with the existing literature. However, the behavior of the energy for the ground state and several excited states is illustrated graphically. Therefore, studying the analytical solution of the N-dimensional Schrödinger equation for the newly proposed Varshni-Hulthen potential could provide valuable information on the quantum mechanics dynamics at atomic and molecular physics and opens new window.











 nueva página del texto (beta)
nueva página del texto (beta)


