1. Introduction
The Hubbard model (HM) was proposed by J. Hubbard in 1963 [1] in order to understand the extensive variety of physical properties of transition metals (TM) with narrow electronic bands, and since then till nowadays it has been used as a basic model to study diverse phenomena, such as antiferromagnetism and charge density waves [2], both phenomena also related to high-T c superconductors. Moreover, it is widely accepted that the single-band Hubbard model is an appropriate starting point to describe the electronic correlations on the copper-oxygen planes of the cuprate superconductors [3]. In particular, the hole superconductivity proposed by J. Hirsch [4], based on a generalized Hubbard model that includes nearest neighbor hopping (t) and the so-called nearestneighbor correlated hopping interaction (∆t), could explain superconducting states with an extended s-symmetry energy gap. However, the inclusion of the next-nearest-neighbor hopping could play a crucial role in the competition between antiferromagnetism and superconductivity in cuprate superconductors [5]. Moreover, phase sensitive experiments have shown that the cuprate superconductors have a d-wave symmetry superconducting gap [6]. In this context, L. A. Pérez and C. Wang showed that when both next-nearest neighbor hopping (t’) and next-nearest-neighbor correlated hopping interaction (∆t 3) are taken into account, a d-wave superconducting ground state can be found in a two-dimensional lattice [7]. This generalized Hubbard model allows to describe many properties of superconducting ground states in a square lattice with different superconducting gap symmetries [8-10].
In a previous work [11], we studied how the critical temperature T c of d-wave superconducting states on a square lattice depends on the electron density (n) and the secondneighbor hopping (t’) for a given set of electron-electron interaction parameters (U,V,∆t,∆t 3). In other words, for each value of t’, we calculated T c (n) and the particular value n op(t’) where T c is maximum is called the optimal density. Moreover, we also studied the particular value n op,sup where the minimum value of T c (n op) is found. This value, which corresponds to the minimum value of the critical temperature among the set formed by the maximum values of T c , has been dubbed the supreme value of T c (T c,max,sup ). Moreover, we have found that the minimum superconducting ground state energy is attained at this particular value n op,sup [11].
By locating n op-sup for a fixed ∆t 3 = 0.05 eV, critical temperatures of T c ≈ 40 K and T c ≈ 100 K, can be found that correspond to La 2−x Sr x CuO4 and YBa2Cu3O7−x with ∆t = 0.1 eV and ∆t = 0.5 eV, respectively [11].
Motivated by this scenario, in this work the critical temperature of systems with an extended s-wave (s *) superconducting gap as a function of n and t’ (for a given set of electron-electron interaction parameters) has been studied. Considering that the d-wave superconducting state arises from the V and ∆t 3 interactions, while the s *-wave one originates from both ∆t and ∆t 3, V will be set to zero to keep a minimum set of parameters. It is worth mentioning that for d-wave superconductors, U does not change the superconducting critical temperature [7,10], whereas for s *-wave superconductors U hinders the superconducting gaps and the critical temperatures [7,10]. In contrast with the d-wave case [11], the results show that, for the s *-wave case, the minimum of T c (n op) it is not attained at the same value of n op (and t’) where the minimum ground state energy is found, although for U = 2 eV, the minimum of T c (n op) and E g are attained close to half filling but at slightly different values of n op. The different behaviors found for d-wave and s *-wave symmetries are related to the fact that, for the latter case the superconducting gap has an isotropic (∆ s ) and anisotropic (∆ s ∗ ) amplitudes.
2. The model
Within the single-band Generalized Hubbard Hamiltonian [10], with on-site electron-electron Coulombic interaction (U), inter-site Coulombic interaction (V ), first-(∆t) and second neighbor (∆t 3) correlated-hopping interactions, the interaction (V k , k0, q) between electrons with antiparallel spins in the reciprocal space can be written as [10,11]:
where q is the wave vector of the centre of mass of the two interacting electrons with relative wave vectors k and k'.
For a square lattice with lattice parameter α, we have [11]:
Within the mean-field BCS formalism [10], we obtain the following two coupled integral equations which determine the superconducting gap ∆ α (k) with symmetry α = s * ,d, and the corresponding chemical potential µ α for a given temperature T and electron density (electrons per lattice site) n:
Here 1BZ refers to the first Brillouin zone of a square lattice, defined as
and E α (k) is the quasi-particle energy given by:
where (ε MF (k)) is the mean field (MF) dispersion relation given by
with:
where t and t’ are the nearest and next-nearest neighbor hopping parameters. Here we take t < 0. Once the electronelectron interaction V k,k’,q of Eq. (1) is replaced into Eq. (4) and the possible superconducting gap solutions with d- and s *-wave symmetries are considered (first column of Table I), we obtain the equations shown in the second column of Table I.
TABLE I Superconducting gap equations for d- and s*-wave symmetries.
| Superconducting gap | Superconducting-gap equation |
|
d-wave |
|
|
s*-wave |
|
For the s *-wave symmetry superconducting gap ∆ s ∗(k) = ∆ s + ∆ s ∗(cos[k x α] + cos[k y α]), ∆ s and ∆ s ∗ denote the isotropic and anisotropic gap amplitudes, respectively, and the integrals I l for l = 0,1,2, are given by
The critical temperature (T c ), can be determined from Eq. (11), or from Eqs. (12) and (13) together with Eq. (5) by considering that ∆ α (T = T c ) = 0. In this case, the equations in Table I, can be reduced to those shown in Table II.
TABLE II Critical temperature equations for d- and s*-wave symmetries.
| Superconducting gap symmetry | Critical temperature equation |
| d-wave |
|
| s*-wave |
|
where
On the other hand, the ground state energy (E g,α ) per site can be obtained from the following equation [12]:
where
and
is the ground state BCS-like wave function for singlet pairs. The probability amplitudes to find the states ⟨k ↑,−k ↓⟩ occupied (unoccupied) are v k −α(u k −α) are given by:
Notice that
3. Results
We investigated the critical temperature as a function of the electron density (n) and the next-nearest neighbor hopping parameter (t’) for a system with an extended s-wave (s *) superconducting gap and V = 0, ∆t = 0.5 eV and ∆t 3 = 0.05 eV. Figure 1 shows T c (n,t’) for U = 2 eV. Notice that the highest values of T c occur at high electron densities n. From these data, the maximum of T c,max as a function of n can be extracted for each value of t’ and the particular value of n(n op) at which this maximum is attained is recorded. These values of T c,max at the optimal doping (n op) are marked with open gray circles in Fig. 1. Figure 2 shows the isotropic ∆ s (n op(t’)) (open gray circles) and anisotropic ∆ s ∗(n op(t’)) (open black circles) superconducting s-wave gap amplitudes at the optimal doping (n op(t’)) for each value of t’ for the same systems shown in Fig. 1. Figure 3 shows the corresponding ground state energies of s *-wave superconducting states at the optimal doping for each value of t’, i.e., E g,s ∗ (n op(t’)), calculated with Eq. (18) with U = 2 eV (open gray circles) and U = 0 (open black circles). For the case with U = 2 eV, T c,max has a minimum at n op = 0.55, whereas E g,s ∗ has a minimum at n op = 0.63. This is in contrast to what happens in the dwave case where both the minimum of the energy and the minimum of T c,max (among the set of maximum T c’,s ) occur at the same value of n op [11]. This could be related to the fact that the s *-wave superconducting gap has two gap amplitudes (∆ s ,∆ s ∗) that at T c become zero at the same time, whereas at T = 0 they could even have different sign. In contrast, the d-wave superconducting gap only has a single superconducting gap amplitude (∆ d ).
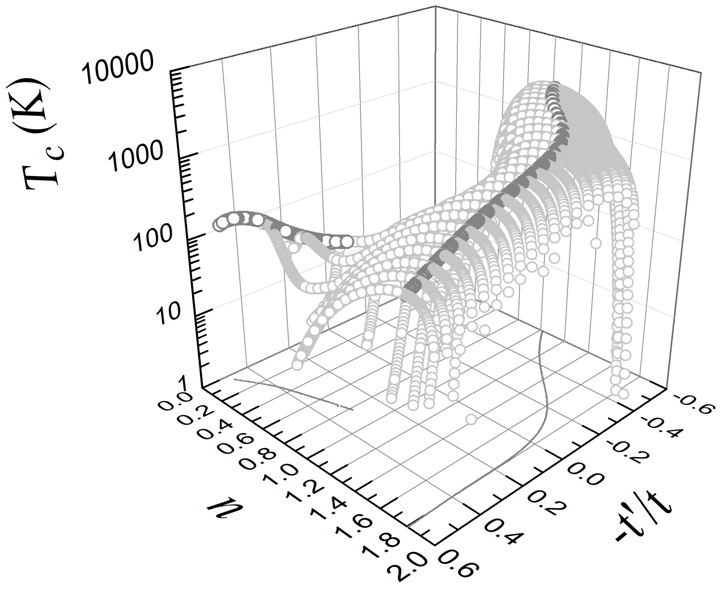
FIGURE 1 The critical temperature (T c ) (open light gray circles) versus the electronic density (n) and the next-nearest neighbor hopping parameter t’ for V = 0, ∆t = 0.5 eV, ∆t 3 = 0.05 eV and U = 2 eV. The gray circles correspond to local maxima (T c,max ) of the critical temperature as a function of n for a given t’. The projections of these curves on the plane n − t’ are marked with small gray dots and the values of n where T c,max occur are the optimal electron density or optimal doping n op.
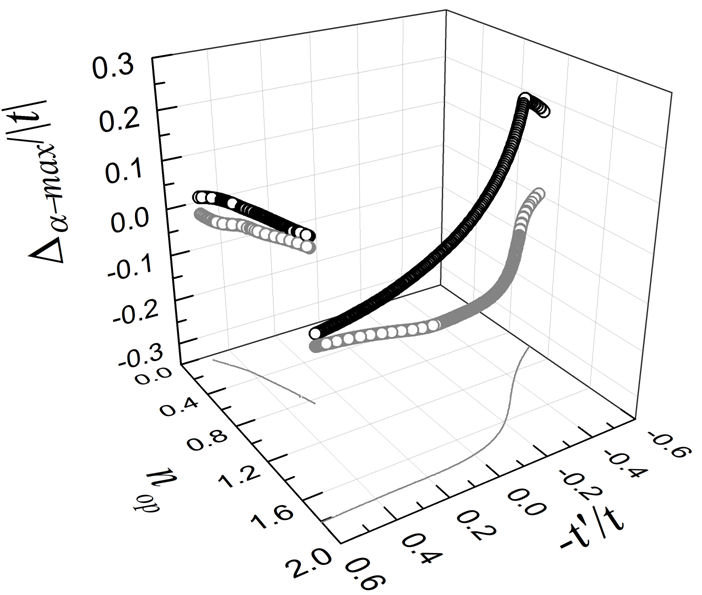
FIGURE 2 Superconducting gap amplitudes ∆ a,max , for α = s (open gray circles) and α = s * (open black circles) evaluated at the optimal carrier concentration or doping n op(t’) considering the same set of parameters as in Fig. 1.
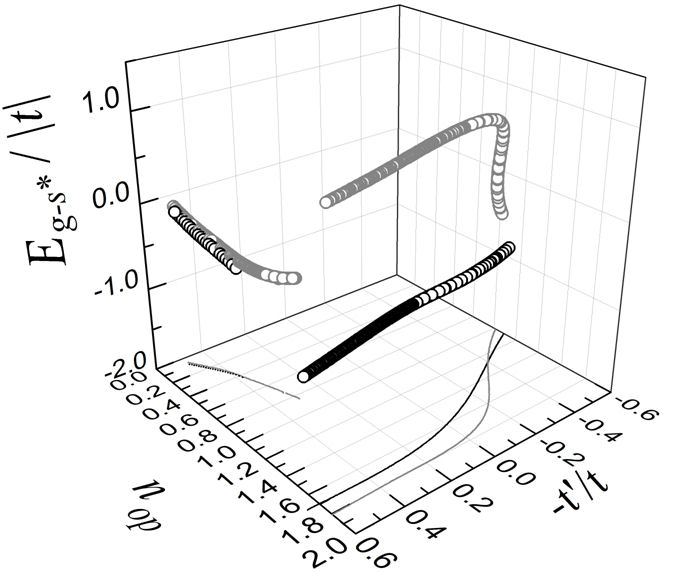
FIGURE 3 Ground state energy (open gray circles) evaluated at the optimal carrier concentration or doping n op(t’) considering the same set of parameters as in Fig. 1 together with the case U = 0 (open black circles).
Tables III and IV summarize the superconducting gap amplitudes ∆ s and ∆ s ∗ , the Fermi energies (E F ), i e., the chemical potentials at T = 0 K, and the ground state energies (E g ) for s *-wave superconducting states with optimal doping (n op) close to those where the minimum of T c,max (n op = 0.55) and the minimum of E g (n op = 0.63) are attained, for systems with U = 2 eV, V = 0, ∆t = 0.5 eV and ∆t 3 = 0.05 eV. In general, for high electron optimal densities T c,max is higher than at low electron densities. However, in the case of d-wave superconducting states with large electron densities (n) above have filling i.e. n ∈ [1,2], which correspond to low hole densities (n h = 2 − n), the Fermi energy at the under doped hole regime (n h < n h,op ) does not lie within the single-electron band and no Fermi surface is encountered. This electron-density zone could be related to the pseudo gap regime of cuprate superconductors which is characterized by the disappearance of Fermi surface [13]. Figure 4 shows the optimal electron density or doping, n op, for s *- (open circles) and d-wave (open squares) superconducting states with the same parameters as in Fig. 2 and for different values of t’. Notice that for t’ ∈ [0.4|t|,0.5|t|], n op(t’) coincide for both s *- and d-wave superconducting states and these occur at low densities, i.e., n op ∈ [0,0.365]. This is due to the fact that for these values of t’, the van Hove singularity of the single-particle electronic density of states (DOS) of a square lattice with first (t) and second neighbor (t’) hoppings at the bottom of the band is enhanced, as shown in the inset of Fig. 4, where the DOS for t’ = 0.45t and n = 0.15 (black line) is depicted. The black arrow in the figure indicates this enhancement in comparison with the DOS for t’ = 0.352|t| and n = 0.55 (grey line). Due to this increment of the DOS, both superconducting states are enhanced at low carrier concentrations close to the bottom of the band. Also, in Fig. 4, the black solid and the gray solid symbols correspond to the minima of T c,max and E g,α , respectively, for each symmetry α. Observe that for d-wave superconductors these two minima (solid squares) occur at almost the same optimal electron density (n op = 0.805) [11], whereas for s *-wave superconductors they occur at different optimal doping n op = 0.55 and n op = 0.63 (solid circles), respectively.
TABLE III Physical properties for s*-wave superconducting states close to minimal of Tc,max for ∆t = 0.5 eV, ∆t3 = 0.05 eV, and U = 2 eV.
| −t’/t | nop | Tc,max (K) | Eg (eV) | ∆s ∗ (eV) | ∆s (eV) | EF (eV) |
| 0.354 | 0.54 | 137.15 | -0.620463 | 0.0140545 | -0.0192207 | -0.759190 |
| 0.352 | 0.55 | 137.03 | -0.623059 | 0.0138245 | -0.01885295 | -0.733963 |
| 0.35025 | 0.56 | 137.04 | -0.625388 | 0.0135944 | -0.01849778 | -0.708160 |
TABLE IV Physical properties for s*-wave superconducting states close to minimal of Eg,s ∗ for ∆t = 0.5 eV, ∆t3 = 0.05 eV, and U = 2 eV.
| −t’/t | nop | Tc,max (K) | Eg (eV) | ∆s ∗ (eV) | ∆s (eV) | EF (eV) |
| 0.33875 | 0.62 | 138.17 | -0.632258 | 0.0122655 | -0.0162540 | -0.555360 |
| 0.3370 | 0.63 | 138.60 | -0.632309 | 0.0120629 | -0.0159037 | -0.529490 |
| 0.3350 | 0.64 | 139.09 | -0.631959 | 0.0118857 | -0.0155746 | -0.504122 |
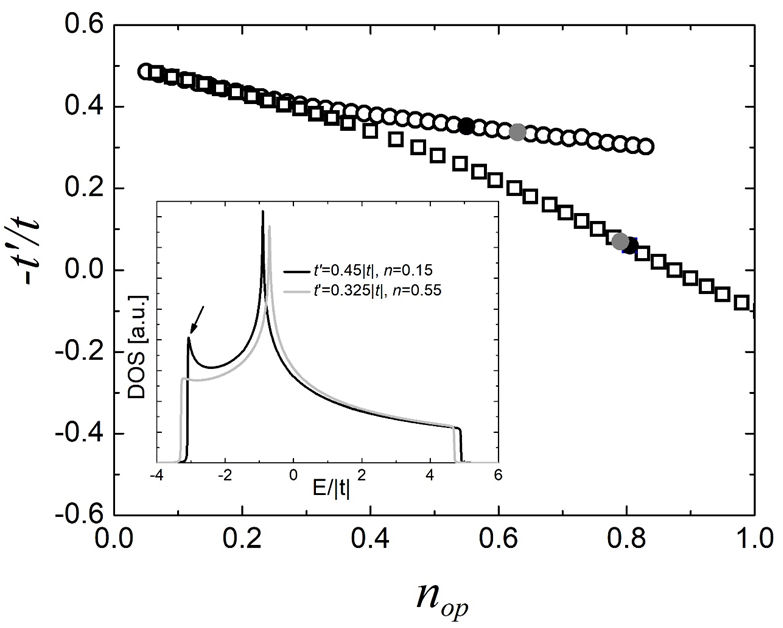
FIGURE 4 Optimal doping as a function of the next-nearestneighbor hopping (n op(t’)) for s *- (open circles) and d-wave (open squares) superconducting states, for the same systems shown in Fig. 2. The solid black and gray circles correspond to the minimum T c,max and Eg,α, respectively. Inset: Single-particle electronic densities of states for systems with two different second-neighbor hoppings t’ and optimal densities n op.
Figure 5 (a) depicts the Fermi surface (FS) for a system with n = 0.55, U = 2.0 eV, V = 0, ∆t = 0.5 eV and ∆t 3 = 0.05 eV which correspond to the minimum of T c,max . Notice that the FS consists of two disconnected parts, one electron-like (circle at the center of the first Brillouin zone) and another one with branches as hole-like FS. Figure 5 (b) shows the single-particle excitation energy gap (∆0) for this s *-wave superconducting state as a function of polar angle φ = tan−1(k y /k x ), which is defined as the minimum value of E s ∗(k) (Eq. 6) along the direction in kspace given by ϕ [10,11]. Observe that, although the superconducting gap has an extended s-wave symmetry given by ∆ s ∗(k) = ∆ s + ∆ s ∗[cos(k x α) + cos(k y α)], ∆0(ϕ) has a very complex pattern with two types of antinodes with different values, the larger ones at ϕ = 0◦, 90◦, 180◦, 270◦, and the lower ones at ϕ = 45, 135◦, 225◦, 315◦, and four nodal lines at ϕ = 30, 60◦, 120◦, 150◦. This complex pattern comes from the interplay between the dispersion relation ε MF (k) (Eq. 7) and ∆ s ∗(k) which appear in E s ∗(k).
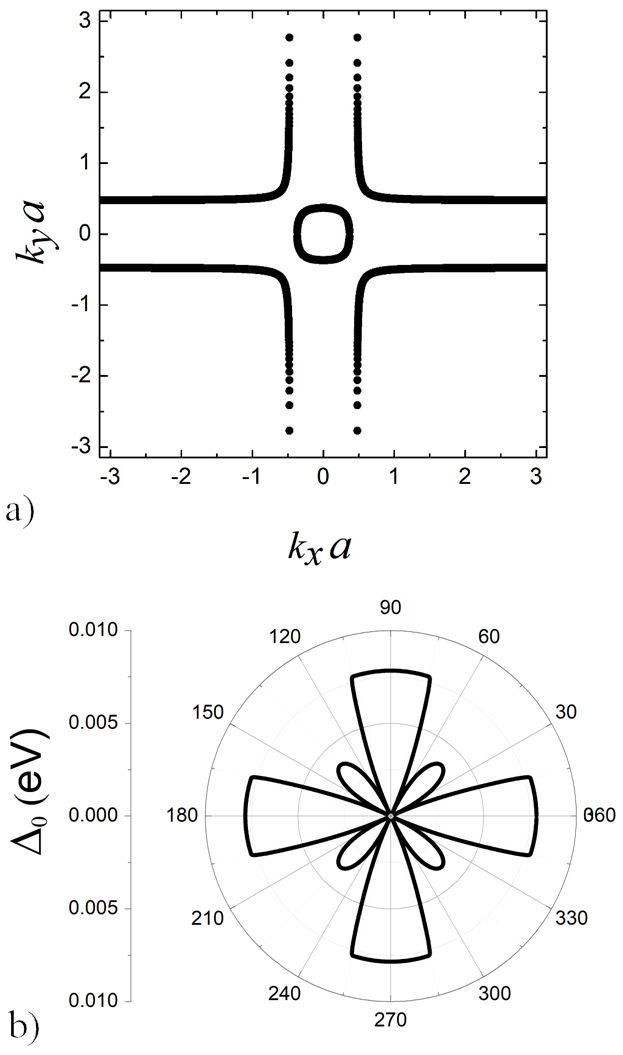
FIGURE 5 a). Fermi surface for a square lattice with n = 0.55, t’ = 0.352|t|, V = 0, ∆t = 0.5 eV, ∆t 3 = 0.05 eV and U = 2 eV. For this case the Fermi energy is E F = −0.734 eV. b). Single particle excitation energy gap (∆0(ϕ)) for an s *-wave superconductor with the same parameters as in Fig. 5. The polar angle (ϕ) is given by ϕ = tan−1(k y /k x ).
4. Conclusions
In summary, within the generalized Hubbard model, we have comparatively studied how the critical temperature and the the ground-state energy of d- and s *-wave superconducting states depend on the electron density n and the first- and second-neighbor hopping parameters t and t’. Within the BCS formalism, the d-wave superconducting properties are calculated by solving the coupled integral Eqs. (5) and (11), whereas the s *-wave superconducting properties are obtained by means of Eq. (5) together with Eqs. (12) and (13). The ground state energy (E g ) was obtained for all the optimal electron concentrations (n op) where T c is maximum for each value of t’. For t’ ∈ [0.4|t|,0.5|t|], n op is located close to the bottom of the band and it is the same for d- and s * -wave systems, since for these values of t’ the van Hove singularity at the bottom of the band is enhanced. Also, at low electron densities, the behavior of s *-wave superconducting states differ from that observed in d-wave superconductors where the minimum of the set of maximum critical temperatures (the supremum of T c,max ) is attained at the same parameter space point (n,t’) where the ground state energy is minimum. This does not occur for s *-wave superconductors where the supremum of T c, max is not attained at the same (n,t’) where the minimum of the ground-state energy is located and, then, a supremum of n op (n op,sup) for s *-wave can’t be defined. For high electron densities close to n = 2, similarly to the d-wave case, the superconducting chemical potential lies outside of the single-particle electronic band and the Fermi surface disappears, which could be related to pseudo gap zone experimentally found for high-T c superconductors [13]. The fact that a n op,sup can be properly defined for d-wave superconductors, and not for s *-wave ones, deserve a further investigation in relation with other symmetries different from d and s *-wave, such as p-wave symmetry, to elucidate if this fact is only a peculiarity of d-wave superconducting states or if it could have more profound implications.
In a future work, we will study the possible superconducting symmetries that can be found in a cubic or tetragonal lattice within the generalized Hubbard model.











 nueva página del texto (beta)
nueva página del texto (beta)


