1. Introduction
In the past few decades, the topic of the fractional differential equations has been the attention of many studies and scientists. This is because many models related to the real world can not be modeled with classical differential equations. Therefore, the fractional differential equations can be used in simulation and modeling of many problems. For example, in electrical, electronic, mechanical, biological and other areas of application related to the real world. For more details see [1,2]. Unfortunately, it is difficult to find an exact solution for most of these models. As a result, the numerical and approximate methods have won the interest of many researchers. Using these methods, researchers were able to study and analyze the dynamic systems that govern these models. There are many such methods including He's variational iteration method [3,4], homotopy analysis [5-7], Fourier spectral methods [8], Adomian's decomposition method [9,10], collocation methods [11-13,15], finite difference schemes [16] and spectral methods [17,18]. Also, there are various other methods that have been applied to many applied models, see for example [19-22]. The model with three types of isothermal chemical reactions is an extension of the model that Scott [23] and colleagues studied. The triple model includes three types of isothermal chemical reactions which incorporate the thermal response capable of supporting complex periodic reactions as well as non-cyclical responses. The relatively stable reactant P is converted into a final product D through the chemical reaction of this model that contains three intermediate chemical species, U, V and W. These chemical reactions are
The governing rate equations for these reactions can be obtained by applying a mass action analysis to (1)-(6),
In dimensionless form, these equations are
Where
are the dimensionless concentrations of the four chemical species and
The importance and novelty of this work is to establish numerical approximate formulas in order to obtain numerical solutions for the proposed model of main importance in chemical applications. These formulas enable many researchers in applied sciences to benefit from them in studying the behavior and characteristics of these systems. After studying the accuracy of these numerical methods presented in this paper, a strong correlation can be made for the numerical results as well as the laboratory results. Also, the strong impetus for this study is due to the fact that many fractional systems do not have exact solutions, so that the behavior of the solutions can be studied, and then the need to create schemes and iterative solutions is required.
In this section, we present the definitions and properties that will be used in this work, [24,25].
Definition 1. For λ > 0, and
Definition 2. For λ> 0, the Liouville-Caputo fractional derivative of order λ, denoted by
Replacing the derivatives d/dt in the dimensionless chemical reaction Eqs. (11)-(14) by the fractional derivatives
In this paper, the numerical scheme and solutions for the fractional isothermal chemical model in the Liouville-Caputo sense are constructed in the second and third sections. For the numerical results presented in the fourth section. The conclusion is presented in the fifth section.
2. Legendre spectral collocation method
Orthogonal functions play a very important role in the development of many numerical methods to address many real-world problems, where the solutions are approximated. By converting fractional differential models into a set of algebraic equations, one of the known numerical methods is used to find an approximate solution to the resulting set of algebraic equations. By using well-known mathematical software, such as Mathematica or Matlab, we can easily find the Legendre coefficients, thereby creating numerical solutions of the fractional model presented in this paper (see [?]).
2.1. Numerical scheme and convergence analysis
We begin by defining the shifted Legendre polynomials on the interval [0,1] with the variable z = 2t - 1. These polynomials have the following property:
where the set {Gk (z) : k = 0,1, 2, …} forms a family of orthogonal Legendre polynomials on the interval [-1,1] (see, for details [30]). The analytic form of the shifted Legendre polynomials of degree s is given by
The function
where the coefficients are given by
Now, we state the following useful theorem.
Theorem 1. [31] Let β(t) be approximated by the shifted Legendre polynomials in Eq. (22). Suppose also that λ > 0. Then
where
2.2. Construction the LSCM
We will now implement the Legendre spectral collocation method to solve numerically the FICEs are given by (17)-(20) as follows [32]
Substituting these expansions into the FICEs (17)-(20) and using (23), we obtain
The Eqs. (25)-(28) are collocated at m nodes tp, p = 0,1,..., m - 1, as follows
In addition, the associated initial conditions can be obtained by using the expansions Eqs. (24). We thus have
Finally, using the Newton-Raphson iteration method, we can solve this system of algebraic equations and get the unknowns
3. Newton polynomial interpolation
In this section, the numerical solutions of the proposed fractional system will be investigated by establishing the iterative formulas and employing them to find the numerical solutions [33]. We apply the fundamental theorem of fractional calculus on (17)-(20) to obtain the following iterative formulas
These Eqs. (37)-(40) can be reformulated as
Using Newton polynomial interpolation as in Ref. [33], we obtain
The integrals in these Newton interpolation formulae are evaluated directly. The numerical solutions of (17)-(20) involving the LC derivative are then given by
where
4. Numerical results and discussion
In this section, the numerical results of the FICEs will be compared through the propped methods in this work. It will be illustrated the comparison of numerical solutions through the figures and tables for different values of λ. Figures 1a)-d) show the comparison of the numerical solutions of FICEs by two proposed methods for λ = 1, m = 21, h = 0.003, L = 10, α = 0.5, ϑ = 0.1, γ = 0.05 and θ = 2. It can be seen from Fig. 1 that the two numerical solutions of FICEs agree in terms of behavior and they are close to each other. In Fig. 2, the absolute errors between the two solutions are shown for the same parameter values as in Fig. 1. It is evident from this figure that the absolute error is very small and the error between the two solutions decreases with the use of more terms in the first method and the use of more iterations in the second method. In Figs. 3 and 4 the calculations are repeated for the same values as in Figs. 1 and 2 but in this case λ = 0.8 was set. This case is very important since the goal of this work is to compare the two different methods of the numerical solutions of FICEs. Also, we notice in these figures that the numerical solutions for the two methods are very close to each other and exhibit the same behavior. Additionally, in Tables I-VIII, the numerical solutions are calculated using the two methods presented in this work, where the calculations of the absolute error in the cases of integer and noninteger order for FICEs were done. From these Tables we also note the accuracy and efficacy of numerical solutions, given the order of the absolute error, where, it ranges between 10-3 and 10-7. The numerical results obtained in this paper agree with the numerical results obtained in Ref. [35].
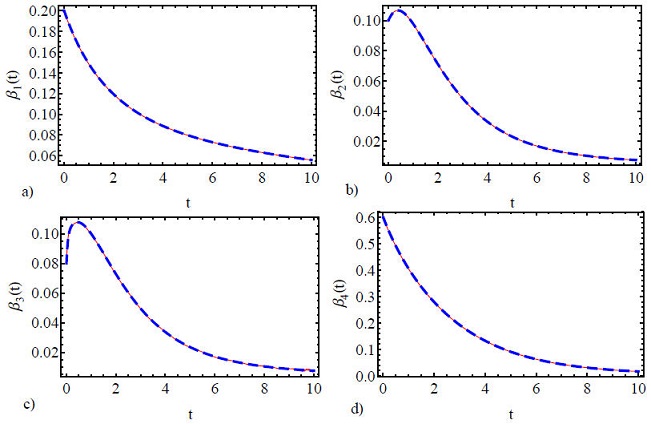
Figure 1 Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0-05, θ = 2, m = 21, h = 0.003, L = 10, λ = 1.

Figure 2 Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0.05, θ = 2, m = 21, h = 0.003, L = 10, λ = 1.

Figure 3 Comparison between the numerical solutions for α = 0.05, ϑ = 2, γ = 0.05, θ = 0.2, m = 21, h = 0.003, L = 10, λ = 0.8. (Blue dashed line: NPI; Red solid line: SCM).

Figure 4 Absolute error between the numerical solutions for α = 0.5, ϑ = 2, γ = 0.05, θ = 0.2, m = 21, h = 0.003, L = 10, λ = 0.8.
Table I Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0.05, θ = 2, m = 21, h = 0.003, L = 10, λ = 1.
| n | β1, SCM(t) | β1, NPI | |β1, SCM(t)-β1, NPI(t)| |
|---|---|---|---|
| 0 | 0.2 | 0.2 | 3.19162 × 10-18 |
| 200 | 0.162359 | 0.162662 | 3.03478×10-4 |
| 400 | 0.137154 | 0.137364 | 2.09480×10-4 |
| 600 | 0.119369 | 0.11952 | 1.51060×10-4 |
| 800 | 0.106315 | 0.106428 | 1.12920×10-4 |
| 1000 | 0.0964151 | 0.096502 | 8.69248×10-5 |
| 1200 | 0.0886838 | 0.0887527 | 6.88986×10-5 |
| 1400 | 0.0824808 | 0.0825367 | 5.59788×10-5 |
| 1600 | 0.0773756 | 0.0774223 | 4.66744×10-5 |
| 1800 | 0.073073 | 0.0731128 | 3.97719×10-5 |
| 2000 | 0.0693664 | 0.0694011 | 3.46306×10-5 |
| 2200 | 0.0661096 | 0.0661403 | 3.07003×10-5 |
| 2400 | 0.0631978 | 0.0632255 | 2.76781×10-5 |
| 2600 | 0.0605554 | 0.0605807 | 2.52558×10-5 |
| 2800 | 0.0581273 | 0.0581506 | 2.33462×10-5 |
| 3000 | 0.0558729 | 0.0558947 | 2.17804×10-5 |
Table II Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0.05, θ = 2, m = 21, h = 0.003, L = 10, λ = 1.
| n | Β2, SCM(t) | Β2, NPI | |β2, SCM(t)-β2, NPI(t)| |
|---|---|---|---|
| 0 | 0.1 | 0.1 | 6.64074 × 10-19 |
| 200 | 0.104424 | 0.104521 | 9.68429 × 10-5 |
| 400 | 0.0891975 | 0.0893786 | 1.81056 × 10-4 |
| 600 | 0.0710369 | 0.0712117 | 1.74852 × 10-4 |
| 800 | 0.0550999 | 0.0552427 | 1.42801 × 10-4 |
| 1000 | 0.0424772 | 0.0425876 | 1.1044 × 10-4 |
| 1200 | 0.0329242 | 0.0330062 | 8.20209 × 10-4 |
| 1400 | 0.0258433 | 0.025904 | 6.07221 × 10-4 |
| 1600 | 0.02064 | 0.0206844 | 4.44039 × 10-5 |
| 1800 | 0.0168194 | 0.0168521 | 3.26876 × 10-5 |
| 2000 | 0.014003 | 0.0140272 | 2.42145 × 10-5 |
| 2200 | 0.0119112 | 0.0119292 | 1.80192 × 10-5 |
| 2400 | 0.0103409 | 0.0103545 | 1.36329 × 10-5 |
| 2600 | 0.00914671 | 0.00915729 | 1.05799 × 10-5 |
| 2800 | 0.00822487 | 0.00823305 | 8.1831 × 10-6 |
| 3000 | 0.00750075 | 0.00750716 | 6.41186 × 10-6 |
Table III Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0.05, θ = 2, m = 21, h = 0.003, L = 10, λ = 1.
| n | Β3, SCM(t) | Β3, NPI | |β3, SCM(t)-β3, NPI(t)| |
|---|---|---|---|
| 0 | 0.08 | 0.08 | 6.93889 × 10-18 |
| 200 | 0.106587 | 0.106335 | 2.51509 × 10-4 |
| 400 | 0.0915829 | 0.0915039 | 7.90304 × 10-5 |
| 600 | 0.0724219 | 0.0729348 | 5.12911 × 10-4 |
| 800 | 0.0566815 | 0.0565243 | 1.57174 × 10-4 |
| 1000 | 0.0431098 | 0.0435182 | 4.08387 × 10-4 |
| 1200 | 0.033895 | 0.0336778 | 2.17171 × 10-4 |
| 1400 | 0.0260243 | 0.026389 | 3.64716 × 10-4 |
| 1600 | 0.0212759 | 0.0210359 | 2.3997 × 10-4 |
| 1800 | 0.0168213 | 0.0171086 | 2.87229 × 10-4 |
| 2000 | 0.0144162 | 0.014216 | 2.00189 × 10-4 |
| 2200 | 0.0118207 | 0.0120696 | 2.48862 × 10-4 |
| 2400 | 0.0107311 | 0.0104603 | 2.7080 × 10-4 |
| 2600 | 0.00881768 | 0.00923811 | 420430 × 10-4 |
| 2800 | 0.00813945 | 0.00829586 | 1.56405 × 10-4 |
| 3000 | 0.00759008 | 0.00755687 | 3.32133 × 10-5 |
Table IV Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0.05, θ = 2, m = 21, h = 0.003, L = 10, λ = 1.
| n | Β4, SCM(t) | Β4, NPI | |β4, SCM(t)-β4, NPI(t)| |
|---|---|---|---|
| 0 | 0.6 | 0.6 | 7.24247 × 10-17 |
| 200 | 0.459588 | 0.460777 | 1.18848 × 10-3 |
| 400 | 0.357414 | 0.358309 | 8.94975 × 10-4 |
| 600 | 0.279207 | 0.279887 | 6.80213 × 10-4 |
| 800 | 0.218143 | 0.218691 | 5.47852 × 10-4 |
| 1000 | 0.17028 | 0.170696 | 4.15683 × 10-4 |
| 1200 | 0.132766 | 0.133105 | 3.38834 × 10-4 |
| 1400 | 0.103528 | 0.103778 | 2.49804 × 10-4 |
| 1600 | 0.0807937 | 0.0810007 | 2.06965 × 10-4 |
| 1800 | 0.063239 | 0.0633866 | 1.47547 × 10-4 |
| 2000 | 0.0496907 | 0.0498149 | 1.2425 × 10-4 |
| 2200 | 0.0393028 | 0.0393879 | 8.50452 × 10-5 |
| 2400 | 0.0313156 | 0.0313926 | 7.6974 × 10-5 |
| 2600 | 0.0252256 | 0.0252684 | 4.27996 × 10-5 |
| 2800 | 0.0205407 | 0.0205778 | 3.70776 × 10-5 |
| 3000 | 0.0169492 | 0.0169816 | 3.24183 × 10-5 |
Table V Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0.05, θ = 2, m = 21, h = 0.003, L = 10, λ = 0.8.
| n | Β1, SCM(t) | Β1, NPI | |β1, SCM(t)-β1, NPI(t)| |
|---|---|---|---|
| 0 | 0.2 | 0.2 | 6.071532×10-18 |
| 200 | 0.159387 | 0.159618 | 2.30538×10-4 |
| 400 | 0.140645 | 0.140746 | 1.00463×10-4 |
| 600 | 0.128397 | 0.128448 | 5.08711×10-5 |
| 800 | 0.119538 | 0.119614 | 7.53509×10-5 |
| 1000 | 0.112869 | 0.112891 | 2.21489×10-5 |
| 1200 | 0.107517 | 0.107565 | 4.81515×10-5 |
| 1400 | 0.103194 | 0.103212 | 1.81214×10-5 |
| 1600 | 0.0995369 | 0.0995646 | 2.77116×10-5 |
| 1800 | 0.0964235 | 0.0964438 | 2.03372×10-5 |
| 2000 | 0.093711 | 0.0937263 | 1.52962×10-5 |
| 2200 | 0.0913054 | 0.091324 | 1.85645×10-5 |
| 2400 | 0.0891566 | 0.0891726 | 1.59665×10-5 |
| 2600 | 0.0872193 | 0.0872242 | 4.89773×10-6 |
| 2800 | 0.0854236 | 0.0854423 | 1.86806×10-5 |
| 3000 | 0.0837683 | 0.0837989 | 3.06043×10-5 |
Table VI Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0.05, θ = 2, m = 21, h = 0.003, L = 10, λ = 0.8.
| n | Β2, SCM(t) | Β2, NPI | |β2, SCM(t)-β2, NPI(t)| |
|---|---|---|---|
| 0 | 0.1 | 0.1 | 2.168404 × 10-18 |
| 200 | 0.100177 | 0.10021 | 3.34464 × 10-5 |
| 400 | 0.0862051 | 0.0862899 | 8.48489 × 10-5 |
| 600 | 0.0734054 | 0.0735147 | 1.09363 × 10-5 |
| 800 | 0.0630386 | 0.0630745 | 3.59705 × 10-5 |
| 1000 | 0.0546495 | 0.0547271 | 7.75792 × 10-5 |
| 1200 | 0.0480308 | 0.0480499 | 1.91111 × 10-5 |
| 1400 | 0.0426172 | 0.0426683 | 5.1118 × 10-5 |
| 1600 | 0.0382718 | 0.0382874 | 1.56726 × 10-5 |
| 1800 | 0.0346542 | 0.0346832 | 2.90497 × 10-5 |
| 2000 | 0.0316701 | 0.0316866 | 1.64846 × 10-5 |
| 2200 | 0.029152 | 0.0291699 | 1.7855 × 10-5 |
| 2400 | 0.0270286 | 0.0270359 | 7.23923 × 10-6 |
| 2600 | 0.0251817 | 0.02521 | 2.82558 × 10-5 |
| 2800 | 0.0236307 | 0.0236344 | 3.72900 × 10-6 |
| 3000 | 0.0222676 | 0.0222641 | 3.52774 × 10-6 |
Table VII Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0.05, θ = 2, m = 21, h = 0.003, L = 10, λ = 0.8.
| n | Β3, SCM(t) | Β3, NPI | |β3, SCM(t)-β3, NPI(t)| |
|---|---|---|---|
| 0 | 0.08 | 0.08 | 3.469447 × 10-18 |
| 200 | 0.102461 | 0.101539 | 9.22728 × 10-4 |
| 400 | 0.088632 | 0.0878293 | 8.02756 × 10-4 |
| 600 | 0.0737625 | 0.0748701 | 1.10762 × 10-3 |
| 800 | 0.0650606 | 0.0642195 | 8.41055 × 10-4 |
| 1000 | 0.0547668 | 0.0556929 | 926154 × 10-4 |
| 1200 | 0.0497238 | 0.0488716 | 8.52278 × 10-4 |
| 1400 | 0.0424371 | 0.0433749 | 9.37781 × 10-4 |
| 1600 | 0.0397346 | 0.0389017 | 8.32905 × 10-4 |
| 1800 | 0.0344243 | 0.0352226 | 7.9836 × 10-4 |
| 2000 | 0.0328434 | 0.0321648 | 6.78616 × 10-4 |
| 2200 | 0.0288634 | 0.0295975 | 7.34043 × 10-4 |
| 2400 | 0.0282892 | 0.0274212 | 8.68008 × 10-4 |
| 2600 | 0.0243502 | 0.0255596 | 1.20941 × 10-3 |
| 2800 | 0.0234221 | 0.0239537 | 5.31656 × 10-4 |
| 3000 | 0.0237056 | 0.0225574 | 1.14814 × 10-3 |
Table VIII Absolute error between the numerical solutions for α = 0.5, ϑ = 0.1, γ = 0.05, θ = 2, m = 21, h = 0.003, L = 10, λ = 0.8.
| n | Β4, SCM(t) | Β4, NPI | |β4, SCM(t)-β4, NPI(t)| |
|---|---|---|---|
| 0 | 0.6 | 0.6 | 7.806256×10-18 |
| 200 | 0.445779 | 0.446702 | 922925×10-4 |
| 400 | 0.365854 | 0.366332 | 4.77962×10-4 |
| 600 | 0.309166 | 0.309406 | 2.39652×10-4 |
| 800 | 0.265732 | 0.2661 | 3.68341×10-4 |
| 1000 | 0.231844 | 0.231963 | 1.18446×10-4 |
| 1200 | 0.204193 | 0.204444 | 2.51442×10-4 |
| 1400 | 0.181822 | 0.181901 | 7.94219×10-4 |
| 1600 | 0.163035 | 0.163197 | 1.61688×10-4 |
| 1800 | 0.147437 | 0.147512 | 7.43729×10-5 |
| 2000 | 0.134137 | 0.134236 | 9.88674×10-5 |
| 2200 | 0.122846 | 0.122905 | 5.93385×10-5 |
| 2400 | 0.113066 | 0.113162 | 9.57111×10-5 |
| 2600 | 0.104737 | 0.104725 | 1.24414×10-5 |
| 2800 | 0.0973151 | 0.0973716 | 5.65149×10-5 |
| 3000 | 0.0907919 | 0.0909248 | 1.32908×10-4 |
5. Conclusion
In this paper, two numerical methods are presented to evaluate the numerical solutions of the fractional isothermal chemical equations. The first method is based on the use of the properties of Legrendre polynomials and collocation method, whereas the second method is constructed with Newton polynomial interpolation and the fundamental theorem of fractional calculus. These two methods are employed to find numerical solutions of the fractional isothermal chemical equations. The numerical solutions were compared by combining the solutions together, as well as calculating the amount of absolute error between the numerical solutions. We found a good compatibility and a very small error order. In future works, we will focus on the use of Newton interpolating polynomial, several special functions (Chebyshev, Bernstein, etc), and the spectral collocation method, besides studying the effects of the fractal-fractional order on the dynamics of isothermal chemical equations. We will also repeat all the above discussions and calculations via to the new operators with nonsingular kernels (see [36-41]).











 nueva página del texto (beta)
nueva página del texto (beta)


