A comprehensive analysis of 19F + 9Be, 12C, 16O, 19F, 27Al, 28,30Si, 40Ca, 54,56Fe, 208Pb, 232Th fusion reactions

Aygun, M.; Cin, H.; Aygun, M.; Cin, H.

doi:10.31349/revmexfis.68.031202

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista mexicana de física

versión impresa ISSN 0035-001X

Rev. mex. fis. vol.68 no.3 México may./jun. 2022 Epub 14-Abr-2023

https://doi.org/10.31349/revmexfis.68.031202

Research

Nuclear Physics

A comprehensive analysis of ¹⁹F + ⁹Be, ¹²C, ¹⁶O, ¹⁹F, ²⁷Al, ^28,30Si, ⁴⁰Ca, ^54,56Fe, ²⁰⁸Pb, ²³²Th fusion reactions

M. Aygun^a

H. Cin^a

^{^a} Department of Physics, Bitlis Eren University, Bitlis, Turkey.

Abstract

We theoretically analyze many fusion experimental data by using ten different density distributions of the ¹⁹F nucleus. The real potentials are obtained by means of the double folding model while the imaginary potentials are established as the Woods-Saxon potential. The theoretical results are compared with the results calculated over one-dimensional Wong formula as well as the experimental data. Thus, alternative density distributions are proposed for the analysis of the experimental data of the ¹⁹F fusion reactions. Additionally, the barrier positions and heights of all the analyzed fusion reactions are calculated for all the density distributions and new analytical expressions for these results are derived. Finally, new pocket formulas giving the imaginary potential depths for fusion cross-section calculations with ¹⁹F are obtained for the first time.

Keywords: Fusion reaction reaction; density distribution; optical model; double folding model

1 Introduction

The fusion reaction is a reaction where light nuclei can form a heavier nucleus. If the two interacting nuclei cross the Coulomb barrier, the fusion reaction can occur. The fusion reaction is one of the reactions studied to obtain information about the structure and properties of interacting nuclei. Thus, a lot of experimental and theoretical studies have been carried out ^[1, ^2]. However, fusion reactions still deserve to be studied in the field of nuclear physics.

¹⁹F is an important nucleus that has been extensively studied both experimentally and theoretically in the context of fusion reactions. In this context, the ¹⁹F + ⁹Be fusion cross section was reported at energies above the Coulomb barrier ^[3]. The experimental data of 1⁹F + ¹²C fusion reaction was measured by Ref. ^[3]. They also investigated the effect of breakup on the fusion reaction, and reported that breakup has not an important influence. Anjos et al.^[4] reported the fusion cross-section of ¹⁹F + ¹⁶O system. They showed that the light heavy-ion fusion cross-sections depended on the entrance channel mass asymmetry. The fusion data of ¹⁹F + ¹⁹F reaction was measured by Ref. ^[4]. The ¹⁹F + ²⁷Al fusion experimental data was presented by Ref. ^[3]. Chiou et al. ^[5] recorded the cross-sections of ¹⁹F + ^28,30Si fusion reactions, and compared the data with the theoretical results obtained using different models. The fusion data of ¹⁹F + ⁴⁰Ca reaction was reported by Ref. ^[4]. The experimental data of ¹⁹F + ^54,56Fe fusion reactions were measured by Ref. ^[6]. They observed that the one-dimensional barrier penetration model did not successfully explain the data. Then, they performed the coupled channel calculations, and obtained agreement results with the experimental data. The fusion experimental data of ¹⁹F + ²⁰⁸Pb was reported by Ref. ^[7]. Finally, the fusion data of ¹⁹F + ²³²Th system was measured ^[8]. We have noticed from these studies that the effect of different density distributions on the ¹⁹F fusion cross-sections has not yet been examined simultaneously.

The nuclear potential is one of the parameters required to explain fusion reactions. With the help of this potential, an accurate analysis of the system can be performed. The double folding model (DFM) is one of the widely used models for this purpose ^[9, ^10, ^11]. It uses the density distributions of the projectile and target nuclei. Therefore, the density distribution is of particular importance in generating the nuclear potential. Recently, Aygun ^[12] examined the effect of different density distributions of ¹⁹F on the elastic scattering cross-sections, and obtained good agreement results with the experimental data. We believe that it would be important and useful to see the effectiveness of these density distributions on the ¹⁹F fusion cross-sections.

In the present study, we first calculate the cross-sections of ¹⁹F + ⁹Be, ¹⁹F + ¹²C, ¹⁹F + ¹⁶O, ¹⁹F + ¹⁹F, ¹⁹F + ²⁷Al, ¹⁹F + ²⁸Si, ¹⁹F + ³⁰Si, ¹⁹F + ⁴⁰Ca, ¹⁹F + ⁵⁴Fe, ¹⁹F + ⁵⁶Fe, ¹⁹F + ²⁰⁸Pb and ¹⁹F + ²³²Th fusion reactions by using ten different density distributions of ¹⁹F. Then, we obtain the fusion cross-sections based on the one-dimensional Wong formula in order to make a comparative study. We compare our results with the one-dimensional Wong results as well as the experimental data. Then, we calculate the barrier positions (R _B) and heights (V_B) for all the analyzed fusion reactions and the density distributions, and derive new analytical expressions for these results. Finally, we acquire for the first time global potential equations that provide the imaginary potential depths for all the analyzed density distributions.

Section 2 presents the calculation procedure which consists of the models and densities. Section 3 states the results and discussion. Section 4 gives the summary and conclusions.

2 Calculation procedure

2.1 Optical model

The optical model possesses two potentials: one real and one imaginary. The DFM produces the real part of the optical model by means of the following equation

V(r→)=∫‍dr→1∫‍dr→2ρP(r→1)ρT(r→2)νNN(r→-r→1+r→2), (1)

where ρP(T)(r←1(2)), respectively are the densities of projectile and target, and νNN is nucleon-nucleon interaction accepted as ^[13]

νNN(r)=7999 exp(-4r)4r-2134 exp(-2.5r)2.5r- 276 1-0.005ELabAp δ(r) MeV. (2)

The imaginary part of the optical model is taken in the Woods-Saxon type

W(r)=-W01+expr-Rwaw, Rw=rw (AP1/3+AT1/3), (3)

where W ₀ is the depth, r _w is the radius, and a _w is diffuseness parameter. The code DFPOT ^[14] is applied in the DFM calculations.

2.2 Fusion cross-sections

In this study, the fusion cross-sections are calculated by using the code FRESCO ^[15] based on the barrier penetration model (BPM). Within the framework of the BPM, the fusion cross-section can be written in the following form

σFus(E)=πk2∑l=0∞‍(2l+1)Tl(E). (4)

Tl(E) is the transmission coefficient, and is given as

Tl(E)=1-Sl2 (5)

where Sl is S-matrix. Tl(E) value is acquired over numerical integration of the following Schrödinger equation ^[2]

d2ul(r)dr2+2μℏ2E-Vtotal(r)ul(r)=0. (6)

2.3 Densities of ¹⁹F projectile

2.3.1 São Paulo (SP), Fermi (2pF), Schechter (S), Moszkowski (M), Jager (J)

SP ^[16], 2pF ^[17], S ^[18], M ^[19] and J ^[20] densities can be taken as the two parameter Fermi

ρ i(r)=ρ0i1+expr-Riai, (i=n,p), (7)

where ρ0i, R_i and a_i parameters are listed in Table I.

Table I The ρ0, R₀ and a values of SP, 2pF, S, M and J densities.

Density	(₀ (fm^-3)	R₀ (fm)	a (fm)	Ref.
SP	(_0n =0.1220860	R_n =2.42011	a_n =0.47460	[16]
	(_0p =0.0891972	R_p =2.64495	a_p =0.46253
pF	(_0n =0.0700497	R_n =2.96218	a_n =0.526	[17]
	(_0p =0.0708402	R_p =2.84187	a_p =0.5129
S	0.154342	2.77514	0.54	[18]
M	0.16	3.06866	0.50	[19]
J	0.17784	2.59	0.564	[20]

2.3.2 Ngô (Ngo)

Ngo density can be formulated as ^[21, ^22]

ρ npr=34πNZA1r0n0p31+expr-C0.55, C=R(1-1R2), (8)

where

R=Nr0nA1/3+Zr0pA1/3A, r0n=1.1375+1.875×10-4A, r0p=1.128 fm (9)

2.3.3 Gupta 1 (G1)

G1 density ^[23, ^24] is given by

ρ ir=ρ0i1+expr-R0iai, ρ0i=3Ai4πR0i31+π2ai2R0i2-1, (10)

where

R0i=0.90106+0.10957Ai-0.0013Ai2+7.71458×10-6Ai3-1.62164×10-8Ai4, (11)

ai=0.34175+0.01234Ai-2.1864×10-4Ai2+1.46388×10-6Ai3-3.24263×10-9Ai4. (12)

2.3.4 Gupta 2 (G2)

G2 density ^[25] based on Eq. (10) is accepted as

R0i=0.9543+0.0994Ai-9.8851×10-4Ai2+4.8399×10-6Ai3-8.4366×10-9Ai4, (13)

ai=0.3719+0.0086Ai-1.1898×10-4Ai2+6.1678×10-7Ai3-1.0721×10-9Ai4. (14)

2.3.5 Wesolowski (W)

W density ^[26] is in the following form ^[27]

ρ0=34πR031+π2a2R02-1, a=0.39 fm, (15)

R0=R'1-(bR')2+13(bR')6+..., (16)

R'=1.2-0.96A1/3N-ZAA1/3, b=π3a. (17)

2.3.6 Hartree-Fock-Bogolubov (HFB)

Neutron and proton densities are obtained over the HFB model considering the BSk2 Skyrme force calculations ^[28]. In this respect, detailed information about the BSk2 force and the HFB model can be found from Refs. ^[29] and ^[30], respectively.

2.4 Densities of target nuclei

In our study, the ⁹Be density is taken as ^[31]

ρ(r)=(A+BC2r2)exp(-C2r2)+(D+EF2r2)exp(-F2r2), (18)

where, A = 0.0651, B = 0.0398, C = 0.5580, D = 0.0544, E = 0.0332 and F = 0.4878.

The densities of ¹²C and ¹⁶O targets are produced by

ρ(r)=(ξ+γr2)exp (-βr2), (19)

where ξ = 0.1644, γ = 0.082003, β = 0.3741 for ¹²C ^[32], and ξ = 0.13173, γ = 0.085058, β = 0.3228 for ¹⁶O ^[33, ^34, ^35].

The density distributions of ²⁷Al, ²⁸Si, ³⁰Si, ⁴⁰Ca, ⁵⁴Fe, ⁵⁶Fe, ²⁰⁸Pb and ²³²Th targets are accepted as the 2pF density shown by

ρ(r)=ρ01+expr-cz, (20)

where ρ0, c and z parameters are given in Table II.

Table II The 2pF density parameters for ²⁷Al, ²⁸Si, ³⁰Si, ⁴⁰Ca, ⁵⁴Fe, ⁵⁶Fe, ²⁰⁸Pb and ²³²Th targets.

Nucleus	(₀ (fm^-3)	c (fm)	z (fm)	Ref.
²⁷Al	0.2015	2.84	0.569	[36]
²⁸Si	0.175	3.15	0.475	[32]
³⁰Si	0.174908	3.17048	0.538603	[25]
⁴⁰Ca	0.169	3.60	0.523	[32]
⁵⁴Fe	0.1699279	4.012	0.5339	[20]
⁵⁶Fe	0.174934	3.971	0.5935	[20]
²⁰⁸Pb	0.1600	6.62	0.551	[36]
²³²Th	0.16477	6.80516	0.559058	[25]

3 Results and Discussion

3.1 Fusion cross-sections

The fusion cross-sections have been calculated for ten different densities of the ¹⁹F nucleus that includes SP, 2pF, Ngo, G1, G2, W, S, M, J and HFB. The changes with the distance of the density distributions can be found in our previous work ^[12]. While the real parts of the optical model potential are obtained using these density distributions, the imaginary parts are assumed as the Woods-Saxon potential. In order to acquire good agreement results with the experimental data, the depth (W₀), radius (r_w) and diffussenes (a_w) parameters of the Woods-Saxon potential are researched at 0.1 and 0.01 step intervals. Additionally, the same potential geometry for all reactions is applied to obtain general expressions of the imaginary potentials. Thus, the r_w and a_w values are accepted as 1.07 fm and 0.75 fm, respectively. Finally, the W₀ values which are determined at the values of r_w and a_w are given in Table III.

Table III The imaginary potential depths (W₀) obtained from the analysis of the fusion reactions. The geometrical parameters are fixed as follows: r_w = 1.07 fm and a_w = 0.75 fm.

Reaction	SP	2pF	Ngo	G1	G2	W	S	M	J	HFB
¹⁹F + ⁹Be	2.60	2.20	2.20	2.50	2.60	2.50	2.20	2.15	2.25	2.45
¹⁹F + ¹²C	16.5	7.50	7.50	12.5	14.0	11.2	8.20	7.50	8.90	11.0
¹⁹F + ¹⁶O	4.80	3.30	3.30	4.00	4.10	4.30	3.30	3.10	3.30	3.90
¹⁹F + ¹⁹F	7.50	3.20	3.50	5.50	6.20	6.50	3.20	3.20	3.40	4.80
¹⁹F + ²⁷Al	4.20	2.70	2.80	3.50	3.55	3.70	2.80	2.70	2.80	3.20
¹⁹F + ²⁸Si	4.00	2.60	2.70	3.60	3.80	3.60	2.70	2.60	2.70	3.20
¹⁹F + ³⁰Si	3.70	2.70	2.70	3.50	3.80	3.60	3.20	2.70	2.70	3.30
¹⁹F + ⁴⁰Ca	8.50	3.70	4.50	7.60	7.00	7.30	4.00	3.60	4.00	5.00
¹⁹F + ⁵⁴Fe	2.80	1.40	1.45	2.10	2.30	2.20	1.40	1.35	1.50	2.10
¹⁹F + ⁵⁶Fe	2.20	1.10	1.10	1.60	1.90	2.10	1.10	1.10	1.20	1.50
¹⁹F + ²⁰⁸Pb	9.00	6.00	6.00	7.60	8.00	9.00	6.00	6.00	7.00	8.00
¹⁹F + ²³²Th	17.5	9.50	9.50	17.0	17.0	16.5	9.50	8.50	9.50	15.5

The cross-section calculations have been carried out for light, medium and heavy mass targets. For light mass targets, we have analyzed the ¹⁹F + ⁹Be, ¹⁹F + ¹²C, ¹⁹F + ¹⁶O, ¹⁹F + ¹⁹F, ¹⁹F + ²⁷Al, ¹⁹F + ²⁸Si and ¹⁹F + ³⁰Si fusion reactions. We have presented the theoretical results for ¹⁹F + ⁹Be in Fig. 1, ¹⁹F + ¹²C in Fig. 2, for ¹⁹F + ¹⁶O in Fig. 3, for ¹⁹F + ¹⁹F in Fig. 4, for ¹⁹F + ²⁷Al in Fig. 5, for ¹⁹F + ²⁸Si in Fig. 6 and for ¹⁹F + ³⁰Si in Fig. 7. In the ¹⁹F + ⁹Be, the results of the density distributions show similar results with each other, and agree with the data. We have observed that the density results of ¹⁹F + ¹²C exhibit similar results with each other, and are in good agreement with the experimental data (within the error limits). For ¹⁹F + ¹⁶O reaction, we have noticed that the density distributions are coherent with the data. We have observed that the results of the ¹⁹F + ¹⁹F and ¹⁹F + ²⁷Al reactions are in good agreement with the experimental data. At the same time, it has been observed that there is a slight difference in the results at small energies. In the ¹⁹F + ²⁸Si reaction, it has been seen that the density distributions fit well the experimental data, and the SP and W densities are slightly better than the other densities. In the ¹⁹F + ³⁰Si reaction, it has been observed that the SP, G1, G2, and HFB results match the experimental data very well. Additionally, it can be said that low energy results, which cannot define the data, have very high experimental error values. Consequently, it can be expressed that the results obtained using the density distributions can explain well the experimental data of ¹⁹F + ⁹Be, ¹⁹F + ¹²C, ¹⁹F + ¹⁶O, ¹⁹F + ¹⁹F, ¹⁹F + ²⁷Al, ¹⁹F + ²⁸Si and ¹⁹F + ³⁰Si fusion reactions, and these density distributions can be evaluated for the theoretical analysis of ¹⁹F fusion reactions.

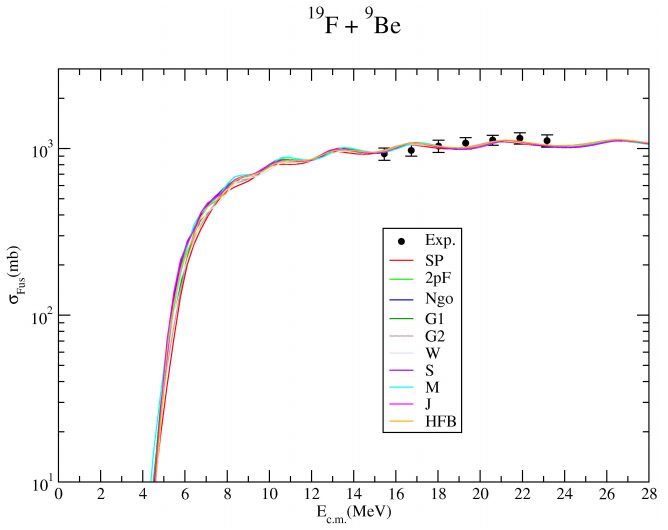
Figure 1 The fusion cross-sections ¹⁹F + ⁹Be system calculated by using different densities of the ¹⁹F nucleus in comparison with the experimental data ^[37].

Figure 2 Same as Fig. 1, but for ¹⁹F + ¹²C reaction. The data are from Ref. ^[37].

Figure 3 Same as Fig. 1, but for ¹⁹F + ¹⁶O reaction. The data are from Ref. ^[37].

Figure 4 Same as Fig. 1, but for ¹⁹F + ¹⁹F reaction. The data are from Ref. ^[37].

Figure 5 Same as Fig. 1, but for ¹⁹F + ²⁷Al reaction. The data are from Ref. ^[37].

Figure 6 Same as Fig. 1, but for ¹⁹F + ²⁸Si reaction. The data are from Ref. ^[37].

Figure 7 Same as Fig. 1, but for ¹⁹F + ³⁰Si reaction. The data are from Ref. ^[37].

We have investigated the ¹⁹F + ⁴⁰Ca, ¹⁹F + ⁵⁴Fe and ¹⁹F + ⁵⁶Fe systems as fusion reactions with medium mass targets. We have compared our results together with the experimental data of ¹⁹F + ⁴⁰Ca in Fig. 8, ¹⁹F + ⁵⁴Fe in Fig. 9 and ¹⁹F + ⁵⁶Fe in Fig. 10. For the ¹⁹F + ⁴⁰Ca reaction, we have observed that the agreement between the theoretical results and the experimental data is good. In the ¹⁹F + ⁵⁴Fe reaction, we have noticed that the theoretical results are in good agreement with the data. For the ¹⁹F + ⁵⁶Fe reaction, we have observed that 2pF, Ngo, S, M and J densities are slightly better than the other densities although the densities fit the data well.

Figure 8 Same as Fig. 1, but for ¹⁹F + ⁴⁰Ca reaction. The data are from Ref. ^[37].

Figure 9 Same as Fig. 1, but for ¹⁹F + ⁵⁴Fe reaction. The data are from Ref. ^[37].

Figure 10 Same as Fig. 1, but for ¹⁹F + ⁵⁶Fe reaction. The data are from Ref. ^[37].

As the fusion reacts with heavy mass targets, we have analyzed the ¹⁹F + ²⁰⁸Pb and ¹⁹F + ²³²Th systems. We have presented the theoretical results of ¹⁹F + ²⁰⁸Pb in Fig. 11 and ¹⁹F + ²³²Th in Fig. 12. For the ¹⁹F + ²⁰⁸Pb and ¹⁹F + ²³²Th reactions, we have observed that the density distributions show an average behavior with the experimental data. It has been seen that the densities for ¹⁹F + ²⁰⁸Pb reaction behave close to each other. Additionally, it has been realized that the HFB density for ¹⁹F + ²³²Th reaction is slightly more compatible with the experimental data compared to the other densities.

Figure 11 Same as Fig. 1, but for ¹⁹F + ²⁰⁸Pb reaction. The data are from Ref. ^[37].

Figure 12 Same as Fig. 1, but for ¹⁹F + ²³²Th reaction. The data are from Ref. ^[37].

3.2 One-dimensional Wong formula

To make a comparative study, we have calculated the fusion cross-sections within the scope of one-dimensional Wong formula. In order to obtain the results, we have applied the Wong formula ^[38] in the following form

σ(E)=ℏωRb22Elog1+exp2πℏωE-Vb, (21)

where V_b , R_b and ℏω, respectively are the barrier height, radius and curvature ^[39] which are listed in Table IV. In order to make a comparative study, we have obtained the Wong formula results for ¹⁹F + ¹²C, ¹⁹F + ¹⁶O, ¹⁹F + ²⁸Si, ¹⁹F + ³⁰Si, ¹⁹F + ⁴⁰Ca, ¹⁹F + ⁵⁶Fe, ¹⁹F + ⁵⁶Fe, ¹⁹F + ²⁰⁸Pb and ¹⁹F + ²³²Th fusion reactions. Then, we have compared the Wong with some density distributions which provides good agreement results with the experimental data in Fig. 13. We have noticed that the results are better than the Wong results in general.

Table IV The R_B (in fm), V_B (in MeV) and hω (in MeV) values evaluated in calculating the ¹⁹F + ¹²C, ¹⁹F + ¹⁶O, ¹⁹F + ²⁸Si, ¹⁹F + ³⁰Si, ¹⁹F + ⁴⁰Ca, ¹⁹F + ⁵⁴Fe, ¹⁹F + ⁵⁶Fe, ¹⁹F + ²⁰⁸Pb and ¹⁹F + ²³²Th fusion cross-sections by using one-dimensional Wong formula.

Reaction	R_B (fm)	V_B (MeV)	hω (MeV)	Ref.
¹⁹F + ¹²C	8.79	8.51	7.50	[4, 40]
¹⁹F + ¹⁶O	8.23	11.21	7.50	[4, 40]
¹⁹F + ²⁸Si	8.72	20.33	7.50	[40]
¹⁹F + ³⁰Si	8.91	20.41	7.50	[40]
¹⁹F + ⁴⁰Ca	8.41	24.09	7.50	[4, 40]
¹⁹F + ⁵⁴Fe	9.43	33.20	3.70	[6]
¹⁹F + ⁵⁶Fe	9.48	33.00	3.66	[6]
¹⁹F + ²⁰⁸Pb	11.8	84.50	4.50	[41]
¹⁹F + ²³²Th	11.92	91.07	4.25	[42]

Figure 13 A comparison of the ¹⁹F + ¹²C, ¹⁹F + ¹⁶O, ¹⁹F + ²⁸Si, ¹⁹F + ³⁰Si, ¹⁹F + ⁴⁰Ca, ¹⁹F + ⁵⁴Fe, ¹⁹F + ⁵⁶Fe, ¹⁹F + ²⁰⁸Pb and ¹⁹F + ²³²Th fusion cross-sections calculated by means of SP, 2pF and Ngo densities and one-dimensional Wong formula.

3.3 Barrier position (R_B) and height (V_B) values

The R_B and V_B are among the desired parameters to be known by the analysis of fusion reactions. For this purpose, we have calculated the R_B and V_B values for all the density distributions and all the fusion reactions investigated with this study. The R_B and V_B values can be determined from the analytical form of the total interaction potential. From this point of view, we obtain the R_B and V_B parameters from the total potential based on the potential parameters used in the theoretical calculations. We have listed our results together with experimental and literature values in Table V. We have observed that our results are consistent with the literature.

Table V The R_B (in fm) and V_B (in MeV) values calculated for SP, 2pF, Ngo, G1, G2, W, S, M, J and HFB densities together with the literature and experimental values for various fusion reactions.

Target	Parameter	SP	2pF	Ngo	G1	G2	W	S	M	J	HFB	Lit.	Exp.
⁹Be	R_B	5.62	5.38	5.38	5.52	5.56	5.60	5.38	5.37	5.38	5.50
	V_B	8.54	8.90	8.88	8.68	8.62	8.60	8.90	8.94	8.88	8.72
¹²C	R_B	8.06	8.44	8.42	8.20	8.14	8.12	8.44	8.48	8.42	8.26	8.79[4]
	V_B	8.93	8.51	8.51	8.76	8.82	8.91	8.51	8.49	8.51	8.73	8.51 [4]
¹⁶O	R_B	8.30	8.68	8.64	8.44	8.38	8.36	8.66	8.71	8.64	8.48	8.23 [4]
	V_B	11.57	11.06	11.06	11.37	11.45	11.55	11.06	11.03	11.07	11.33	11.21 [4]
¹⁹F	R_B	8.34	9.06	9.02	8.62	8.50	8.46	9.04	9.14	9.00	8.70	8.30 [4]
	V_B	12.92	11.86	11.88	12.48	12.65	12.86	11.87	11.80	11.90	12.40	12.44 [4]
²⁷Al	R_B	8.82	9.16	9.14	8.94	8.88	8.88	9.14	9.20	9.12	8.98	8.40 [4]	9.06 [47]
	V_B	17.59	16.92	16.94	17.32	17.43	17.52	16.93	16.87	16.95	17.26	17.54 [4]	17.95 [47]
²⁸Si	R_B	8.68	9.04	9.02	8.82	8.76	8.74	9.02	9.08	9.00	8.86	8.72 [40]	9.05 [47]
	V_B	19.33	18.55	18.56	19.02	19.15	19.26	18.55	18.50	18.57	18.95	20.33 [40]	19.31 [47]
³⁰Si	R_B	8.94	9.28	9.26	9.06	9.02	9.00	9.28	9.32	9.24	9.10	8.91 [40]	9.18 [47]
	V_B	18.74	18.03	18.05	18.46	18.57	18.67	18.04	17.98	18.05	18.40	20.41 [40]	19.05 [47]
⁴⁰Ca	R_B	9.10	9.44	9.42	9.22	9.16	9.18	9.42	9.48	9.40	9.26	8.41 [4]
	V_B	26.33	25.36	25.39	25.96	26.11	26.22	25.38	25.29	25.41	25.86	24.09 [4]
⁵⁴Fe	R_B	9.44	9.78	9.74	9.56	9.50	9.52	9.76	9.82	9.72	9.60	9.43 [6]
	V_B	33.06	31.90	31.94	32.61	32.80	32.92	31.92	31.81	31.96	32.49	33.2 [6]
⁵⁶Fe	R_B	9.62	9.94	9.92	9.74	9.68	9.70	9.92	9.98	9.90	9.78	9.48 [6]
	V_B	32.36	31.28	31.33	91.95	32.12	32.22	31.31	31.20	31.35	31.84	33.0 [6]
²⁰⁸Pb	R_B	11.60	11.90	11.88	11.70	11.66	11.68	11.88	11.96	11.86	11.76	11.80 [41]	11.25 [48]
	V_B	85.74	83.41	83.54	84.87	85.24	85.35	83.49	83.19	83.61	84.59	84.50 [41]	87.44 [48]
²³²Th	R_B	11.80	12.10	12.06	11.90	11.84	11.88	12.08	12.14	12.04	11.94	11.92 [42]	11.46 [49]
	V_B	92.68	90.22	92.36	91.76	92.15	92.26	90.30	89.98	90.44	91.46	91.07 [42]	89.50 [49]

It is helpful to formulate the R _B and V _B parameters calculated in the theoretical analysis of fusion reactions. As known from the literature ^[38, ^3, ^43, ^44, ^45, ^46], the R _B depends on the size of the colliding systems. Thus, the Eq. (22) can be obtained when the R _B is fitted in the context of (AP1/3+AT1/3) terms. Additionally, V _B parameter is linearly dependent on the (ZP+ZT)/(AP1/3+AT1/3) term, and Eq. (23) can be acquired for the V _B . Thus, new analytical expressions of the R_B and V_B parameters can be written in the following form

RB=1.14093AP13+AT13+2.0083 fm (22)

VB=1.02636ZPZTAP1/3+AT1/3-2.85701 MeV (23)

3.4 New pocket formulas of the imaginary potential

It is useful to determine the potential parameters used in the theoretical analysis of fusion reactions. A pocket formula giving the imaginary potential depth would be helpful in describing the fusion cross-sections by using the DFM. We have realized that such an equation is absent for these densities when we have examined the fusion reactions with the ¹⁹F nucleus. To obtain a pocket formula for the W ₀ values determined using the density distributions, we have used the same potential geometry accepted for all the reaction and the densities as well as the W ₀ values given in . In this context, the equations should depend on the W ₀ values together with the charge (Z _T) and the mass (A_T) numbers of the target. So the Eqs. (24)-(33) can be obtained by fitting the W ₀ values given in at r_w = 1.07 fm and a_w = 0.75 fm values. We would like to point out here that we do not get precise expressions. We simply propose new equations that give their imaginary potential depths by taking a different approach to the analysis of fusion reactions. Thus, we have acquired for the first time ten different potential equations for ten different densities by using the potential parameters that are determined in the cross-section calculations. These equations are formulated as

SP density⇒WSP=3.61+0.55ZTAT1/3, (24)

2pF density⇒W2pF=1.75+0.34ZTAT1/3 (25)

Ngo density⇒WNgo=1.90+0.34ZTAT1/3 (26)

G1 density⇒WG1=2.34+0.59ZTAT1/3 (27)

G2 density⇒WG2=2.77+0.57ZTAT1/3 (28)

W density⇒WW=2.22+0.63ZTAT1/3, (29)

S density⇒WS=2.00+0.32ZTAT1/3, (30)

M density⇒WM=1.88+0.30ZTAT1/3 (31)

J density⇒WJ=1.96+0.35ZTAT1/3 (32)

HFB density⇒WHFB=1.76+0.59ZTAT1/3 (33)

where Z_T and A_T are atomic and mass numbers of target, respectively. We would like to point out that these equations are approximate expressions.

4 Summary and Conclusions

We have analyzed the cross-sections of ¹⁹F + ⁹Be, ¹⁹F + ¹²C, ¹⁹F + ¹⁶O, ¹⁹F + ¹⁹F, ¹⁹F + ²⁷Al, ¹⁹F + ²⁸Si, ¹⁹F + ³⁰Si,¹⁹F + ⁴⁰Ca, ¹⁹F + ⁵⁴Fe, ¹⁹F + ⁵⁶Fe, ¹⁹F + ²⁰⁸Pb and ¹⁹F + ²³²Th fusion reactions by using ten type densities of the ¹⁹F nucleus. We have obtained good agreement with the experimental data. Thus, we have proposed alternative density distributions for the theoretical analysis of the ¹⁹F fusion reactions.

In the present study, we have also calculated the R_B and V_B values for all the density distributions and all the fusion reactions. Additionally, we have derived new equations which give the R_B and V_B parameters.

Finally, we have produced new and practical pocket formulas of imaginary potentials for ten different densities of the ¹⁹F nucleus. We believe that the formulas would be helpful in understanding the mechanism of fusion reactions induced by the ¹⁹F nucleus.

Acknowledgements

The authors would like to thank the referee for useful comments.

References

[1] M. Aygun and Z. Aygun, A comprehensive analysis of 9Li +70 Zn fu- sion cross section by using proximity potentials, temperature dependent density distributions and nuclear potentials, Rev. Mex. Fis. 65 (2019) 573, https://doi.org/10.31349/revmexfis.65.573. [ Links ]

[2] G. Kocak, M. Aygun, A theoretical analysis of the cross sections of 18;19;20O +12 C fusion reactions by using different density distributions, Nucl. Phys. A 1003 (2020) 122015, https://doi.org/10.1016/j.nuclphysa.2020.122015. [ Links ]

[3] R. M. Anjos et al., No evidence of break-up effects on the fusion of 9Be with medium-light nuclei, Phys. Lett. B 534 (2002) 45, https://doi.org/10.1016/S0370-2693(02)01554-X. [ Links ]

[4] R. M. Anjos et al., Effect of the entrance channel mass asymmetry on the limitation of light heavy-ion fusion cross sections, Phys. Rev. C 42 (1990) 354, https://doi.org/10.1103/PhysRevC.42.354. [ Links ]

[5] M. S. Chiou, M. W. Wu, N. Easwar and J. V. Maher, Complete fusion of 19F with Al and Si isotopes, Phys. Rev. C 24 (1981) 2507, https://doi.org/10.1103/PhysRevC.24.2507. [ Links ]

[6] H. Funaki and E. Arai, Anomaly in the 15N, 16O, 19F +54;56 Fe fusion cross sections around the Coulomb barrier energy, Nucl. Phys. A 556 (1993) 307, https://doi.org/10.1016/0375-9474(93)90353-Y. [ Links ]

[7] D. J. Hinde, A. C. Berriman, M. Dasgupta, J. R. Leigh, J. C. Mein, C. R. Morton and J. O. Newton, Limiting angular momentum for statistical model de- scription of fission, Phys. Rev. C 60 (1999) 054602, https://doi.org/10.1103/ PhysRevC.60.054602. [ Links ]

[8] S. Kailas et al., Fission fragment angular distributions for the system 19F+232Th, Phys. Rev. C 43 (1991) 1466, https://doi.org/10.1103/PhysRevC.43.1466. [ Links ]

[9] Z. Gao-Long and L. Xiao-Yun, Double folding model calculation applied to fusion reactions, Chin. Phys. C 32 (2008) 812, https://doi.org/10.1088/1674- 1137/32/10/009. [ Links ]

[10] I. I. Gontchar, D. J. Hinde, M. Dasgupta and J. O. Newton, Double fold- ing nucleus-nucleus potential applied to heavy-ion fusion reactions, Phys. Rev. C 69 (2004) 024610, https://doi.org/10.1103/PhysRevC.69.024610. [ Links ]

[11] M. Rashdan, Folding model description of 16O+154Sm fusion reaction, J. Phys. G: Nucl. Part. Phys. 22 (1996) 139, https://doi.org/10.1088/0954- 3899/22/1/013. [ Links ]

[12] M. Aygun, A Comprehensive Description of 19F Elastic Scattering by 12C, 16O, 66Zn, 159Tb, and 208Pb Target Nuclei, Braz. J. Phys. 49 (2019) 760, https://doi.org/10.1007/s13538-019-00680-7. [ Links ]

[13] G. R. Satchler and W.G. Love, Folding model potentials from realistic interactions for heavy-ion scattering, Phys. Rep. 55 (1979) 183, https://doi.org/10.1016/0370-1573(79)90081-4. [ Links ]

[14] J. Cook, DFPOT-a program for the calculation of double folded potentials, Commun. Comput. Phys. 25 (1982) 125. [ Links ]

[15] I.J. Thompson, Coupled reaction channels calculations in nuclear physics, Comput. Phys. Rep. 7 (1988) 167. [ Links ]

[16] L. C. Chamon et al., Toward a global description of the nucleus-nucleus interaction, Phys. Rev. C 66 (2002) 014610, https://doi.org/10.1103/PhysRevC.66.014610. [ Links ]

[17] W. M. Seif and H. Mansour, Systematics of nucleon density distributions and neutron skin of nuclei, Int. J. Mod. Phys. E 24 (2015) 1550083, https://doi.org/10.1142/S0218301315500834. [ Links ]

[18] H. Schechter and L. F. Canto, Proximity formulae for folding potentials, Nucl. Phys. A 315 (1979) 470, https://doi.org/10.1016/0375-9474(79)90623-7. [ Links ]

[19] S. A. Moszkowski, Energy dependence of the ion-ion potential with a simplified energy density method, Nucl. Phys. A 309 (1978) 273, https://doi.org/10.1016/0375-9474(78)90548-1. [ Links ]

[20] C. W. De Jager, H. De Vries and C. De Vries, Nuclear charge- and magnetization-density-distribution parameters from elastic electron scattering, At. Data Nucl. Data Tables 14 (1974) 479, https://doi.org/10.1016/S0092-640X(74)80002-1. [ Links ]

[21] C. Ngô et al., Properties of heavy ion interaction potentials calculated in the energy density formalism, Nucl. Phys. A 252 (1975) 237, https://doi.org/10.1016/0375-9474(75)90614-4. [ Links ]

[22] H. Ngô and C. Ngô, Calculation of the real part of the interaction potential between two heavy ions in the sudden approximation,Nucl. Phys. A 348 (1980) 140. https://doi.org/10.1016/0375-9474(80)90550-3. [ Links ]

[23] R. K. Gupta, D. Singh and W. Greiner, Semiclassical and microscopic calculations of the spin-orbit density part of the Skyrme nucleus-nucleus interac- tion potential with temperature effects included, Phys. Rev. C 75 (2007) 024603, https://doi.org/10.1103/PhysRevC.75.024603. [ Links ]

[24] O. N. Ghodsi and F. Torabi, Comparative study of fusion barriers using Skyrme interactions and the energy density functional, Phys. Rev. C 92 (2015) 064612, https://doi.org/10.1103/PhysRevC.92.064612. [ Links ]

[25] R. K. Gupta, D. Singh, R. Kumar and W. Greiner, Universal functions of nuclear proximity potential for Skyrme nucleus-nucleus interaction in a semiclassical approach, J. Phys. G: Nucl. Part. Phys. 36 (2009) 075104, https://doi.org/10.1088/0954-3899/36/7/075104. [ Links ]

[26] E. Wesolowski, The RMS radii of the charge distribution in nuclei, J. Phys. G: Nucl. Part. Phys. 11 (1985) 1401, https://doi.org/10.1088/0305- 4616/11/8/008. [ Links ]

[27] N. K. Dhiman, Role of Different Model Ingredients in the Exotic Cluster- Decay of 56Ni, Ukr. J. Phys. 57 (2012) 796, https://doi.org/10.15407/ujpe57.8.796. [ Links ]

[28] http://www-nds.iaea.org/ripl-2.html. [ Links ]

[29] S. Goriely, M. Samyn, P.-H. Heenen, J. M. Pearson and F. Tondeur, Hartree-Fock mass formulas and extrapolation to new mass data, Phys. Rev. C 66 (2002) 024326, https://doi.org/10.1103/PhysRevC.66.024326. [ Links ]

[30] M. Samyn, S. Goriely , P.-H. Heenen, J. M. Pearson and F. Tondeur, A Hartree-Fock-Bogoliubov mass formula, Nucl. Phys. A 700 (2002) 142, https://doi.org/10.1016/S0375-9474(01)01316-1. [ Links ]

[31] V. Hnizdo, J. Szymakowski, K. W. Kemper, and J. D. Fox, Folding-model description of elastic and inelastic scattering of 9Be by 40;44Ca and 39K at 40 MeV, Phys. Rev. C 24 (1981) 1495, https://doi.org/10.1103/PhysRevC.24.1495. [ Links ]

[32] M. El-Azab Farid and M. A. Hassanain, Density-independent folding anal- ysis of the 6;7Li elastic scattering at intermediate energies, Nucl. Phys. A 678 (2000) 39, https://doi.org/10.1016/S0375-9474(00)00313-4. [ Links ]

[33] G. Kocak, M. Karakoc, I. Boztosun and A. B. Balantekin, Effects of ff-cluster potentials for the 16O +16 O fusion reaction and S factor, Phys. Rev. C 81 (2010) 024615, https://doi.org/10.1103/PhysRevC.81.024615. [ Links ]

[34] S. Qing-biao, F. Da-chun and Z. Yi-zhong, Neutron relativistic phe- nomenological and microscopic optical potential, Phys. Rev. C 43 (1991) 2773, https://doi.org/10.1103/PhysRevC.43.2773. [ Links ]

[35] H. F. Ehrenberg, R. Hofstadter, U. Meyer-Berkhout, D.G. Ravenhall and S. E. Sobottka, High-Energy Electron Scattering and the Charge Distribution of Carbon-12 and Oxygen-16, Phys. Rev. 113 (1959) 666, https://doi.org/10.1103/PhysRev.113.666. [ Links ]

[36] S. Hossain, M. N. A. Abdullah, Md. Z. Rahman, A. K. Basak and F. B. Malik, Non-monotonic potentials for 6Li elastic scattering at 88 MeV, Phys. Scr. 87 (2013) 015201, https://doi.org/10.1088/0031-8949/87/01/015201. [ Links ]

[37] http://nrv.jinr.ru/nrv/ [ Links ]

[38] C. Y. Wong, Interaction Barrier in Charged-Particle Nuclear Reactions, Phys. Rev. Lett. 31 (1973) 766, https://doi.org/10.1103/PhysRevLett.31.766. [ Links ]

[39] A. B. Balantekin and N. Takigawa, Quantum tunneling in nuclear fusion, Rev. Mod. Phys. 70 (1998) 77, https://doi.org/10.1103/RevModPhys.70.77. [ Links ]

[40] Q. Haider and F. B. Malik, Barrier penetration calculation of heavy-ion fusion cross sections in the above- and sub-barrier regions, J. Phys. G: Nucl. Phys. 12 (1986) 537, https://doi.org/10.1088/0305-4616/12/6/012. [ Links ]

[41] L. F. Canto, P. R. S. Gomes, J. Lubian, L. C. Chamon and E. Crema, Dynamic effects of breakup on fusion reactions of weakly bound nuclei, Nucl. Phys. A 821 (2009) 51, https://doi.org/10.1016/j.nuclphysa.2009.02.001. [ Links ]

[42] H. C. Manjunatha and K. N. Sridhar, Fusion barrier characteristics of actinides, Nucl. Phys. A 971 (2018) 83, https://doi.org/10.1016/j.nuclphysa.2018.01.016. [ Links ]

[43] P. R. Christensen and A. Winther, The evidence of the ion-ion potentials from heavy ion elastic scattering, Phys. Lett. B 65 (1976) 19, https://doi.org/10.1016/0370-2693(76)90524-4. [ Links ]

[44] D. G. Kovar et al., Systematics of carbon- and oxygen-induced fusion on nuclei with 12 ≤ A ≤ 19, Phys. Rev. C 20 (1979) 1305, https://doi.org/10.1103/PhysRevC.20.1305. [ Links ]

[45] M. Ismail and M. M. Osman, Real part of the ion-ion interaction potential by use of the Negele realistic nucleon-nucleon force, Phys. Rev. C 24 (1981) 458, https://doi.org/10.1103/PhysRevC.24.458. [ Links ]

[46] H. C. Manjunatha and K. N. Sridhar, Semi empirical formula for fusion barriers of nuclei with 1 ≤ Z ≤ 20, Indian J. Phys. 95 (2021) 935, https://doi.org/10.1007/s12648-020-01756-w. [ Links ]

[47] S. K. Gupta and S. Kailas, Rapid Communication Fusion barriers for heavy-ion systems, Phys. Rev. C 26 (1982) 747, https://doi.org/10.1103/PhysRevC.26.747. [ Links ]

[48] M. Liu et al., Applications of Skyrme energy-density functional to fu- sion reactions spanning the fusion barriers, Nucl. Phys. A 768 (2006) 80, https://doi.org/10.1016/j.nuclphysa.2006.01.011. [ Links ]

[49] A. K. Mohanty, S. V. S. Sastry, S. K. Kataria and V. S. Ramamurthy, Experimental determination of energy-dependent barriers for fusion, Phys. Rev. C 46 (1992) 2012, https://doi.org/10.1103/PhysRevC.46.2012. [ Links ]

Received: July 05, 2021; Accepted: October 30, 2021

This is an open-access article distributed under the terms of the Creative Commons Attribution License