1. Introduction
Semiconductors are used in the vast majority of modern electronic devices. As a result, plenty of research is being conducted to improve their electronic and optical properties with this ever-increasing number of available materials; it is becoming increasingly important to predict the optical properties of new materials in order to determine their usability in optoelectronic devices such as semiconductor lasers or solar cells [1]. III — N compounds are direct band gap energy (Eg) ranging from 0.7 eV for InN, 3.42 eV for GaN, and 6.2 eV for AlN. They can be used at high-temperature, high-frequency, and high-power microelectronic devices. In particular, the GaN is an excellent compound, due to its thermal stability, high thermal conductivity, strong bonding, and distinguished structural, physic-chemical properties [2]. Of particular importance from theoretical and experimental viewpoints, BBiN and Gd doped III — N have been studied in detail by Sam et al., and Amiri et al., respectively [3, 4]. These materials hold enormous promise in optoelectronic and spintronic applications. The electronic configuration of each lanthanide RE element is often denoted as [Xe]4f n, where [Xe] is the electronic configuration of xenon and n is the number of electrons in the inner 4f shell. When incorporated into a host material, the RE atom tends to form a trivalent ion (RE3+). An interesting aspect of these compounds is the occurrence of localized strongly correlated 4f electrons, the treatment of which presents a challenge to band-structure theory [5]. The incorporation of rare-earth elements into III — N is of significant interest for different industrial applications because of their temperature independence and stable emission together with the possibility of optical or electrical excitation [6, 7]. Rare-Earth elements doped III — V are arguably among of the most studied in optical-electronic devices using principles of band gap engineering and quantum confinement. Their applications spanning from a laser, light-emitting diode (LED), vertical-cavity surface-emitting lasers (VCSELs), and quantum-confined Stark effect (QCSE) [8]. The cause of energy loss by transmission or thermalization of photons is related to the shift between the incident solar spectrum and the band gap of most solar cells. The photon conversion strategies such as downconversion, upconversion, and downshifting are possible technologies to increase the efficiency of solar cells. In this regard, trivalent lanthanide ion-doped luminescent materials have attracted great interest due to their promising application as spectral converters [9, 10, 11]. Er-doped III — N materials have been investigated using different growth methods such as ion implantation; Steckl et al. [12] have reported on the fabrication of GaN-based display materials doped with various high concentrations of rare-earth ions and have fabricated electroluminescent devices by molecular beam epitaxy (MBE). Altahtamouni et al.[13], have synthesized Er-doped GaN quantum well structures by metal organic chemical vapor deposition (MOCVD) [13]. This was the motivation for the theoretical study of electronic, optic, and transport properties of both bulk materials heterostructure ErGaN/ErN where the barrier and well crystallize in wurtzite and zinc-blind structure, respectively. Our calculations are based on the GGA+U method with a spin-orbit coupling effect. The structural band, optical parameters, and transport properties are calculated. The rest of the paper is organized as follows: Section 2 provides a brief overview of the computational method used. The detailed electronic properties are discussed in Sec. 3.1. Section 3.2 goes over the optical properties and 3.3 discusses transport properties. Finally, Sec. 4 concludes the paper.
2 Computational details
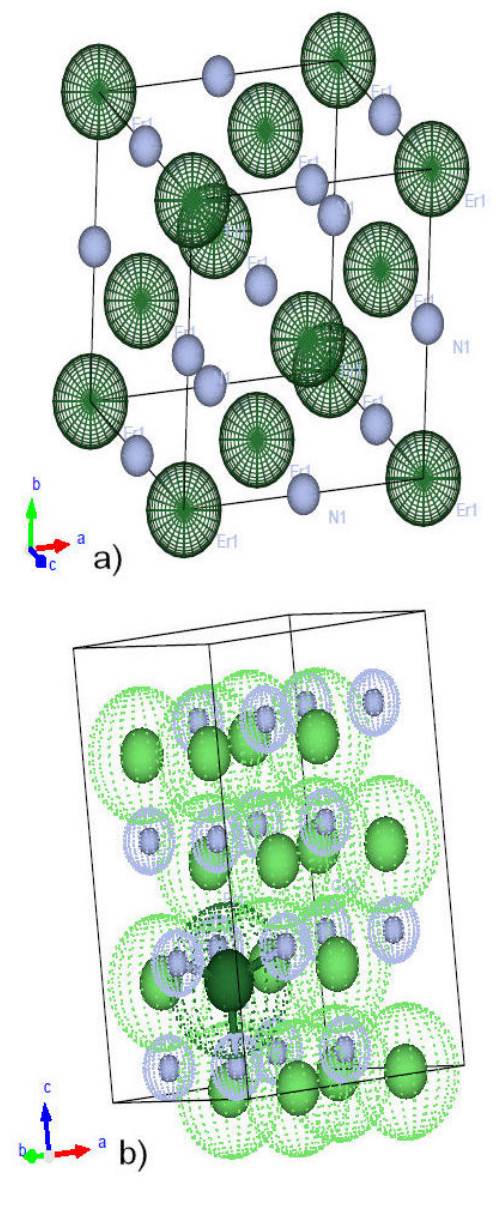
We have investigated the electronic, optical and transport properties of ErN and ErGaN bulk materials shown in Fig. 1, based on DFT [14, 15] using the FP-LAPW method [16, 17] as implemented in the Wien2k code [18]. To calculate the exchange correlation potential, the GGA+U approach wasutilized with a spin-orbit coupling effect, we have used the Hubbard potential U = 8 eV and J = 0 eV for 4f electrons of Er as already reported by Harmon et al. [19], and modified Becke-Jonson approximation (mBJ) [20]. The wurtzite structure of GaN contains 16 atoms, 8 atoms of Ga and 8 atoms of N, one atom of Ga was substituted by one Er atom, to obtain the ErGaN corresponding to a doping concentration 0.125 % of Er. The wave functions are expanded into planes waves in the interstitial region with a cut-off K max = 8 / RMT where RMT has the smallest of all MT sphere radii and K ma is the plane wave cut-off structures ErN and ErGaN we used 2000 and 200 K-points, respectively, in the irreducible Brillouin Zone (IBZ) for our calculation. The BoltzTraP code [21] was used to calculate thermoelectric (TE) properties from ab-initio data using the semi-classical Boltzmann transport theory within the constant relaxation time and rigid band approximations.
3 Results and discussion
3.1 Electronic properties
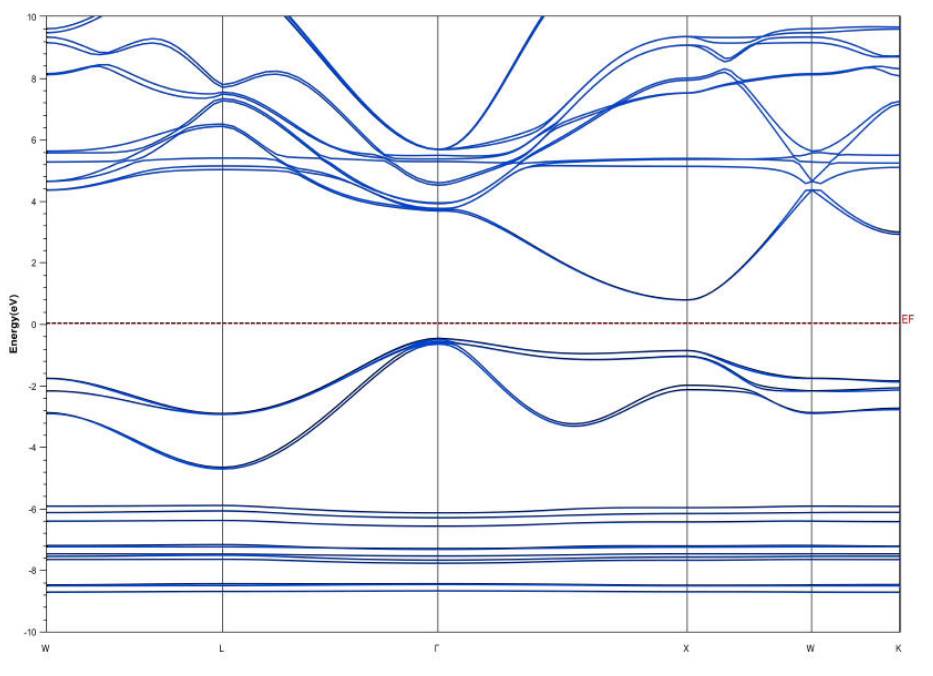
It is interesting to note that ErN turns out to be a semiconductor for the majority spin based on the band structure shown Fig. 2. An indirect band gap at 0.79 eV, with the valence band maximum (VBM) can be seen at point
Total and partial spin polarized density of states of ErN are shown in Fig. 4. The valence bands are dominated by the 4f shell of Er states in the region ranging from -9 to -7.5 eV and by the 5p shell of N states from -.35 to -1.5 eV. The bottom of the conduction band is dominated by 4f in range 4.5 to 5.5 eV. For the total DOS, the valence band is dominated by majority spin; in contrast, the conduction band is dominated by minority spin. The DOS of Er0.125 Ga0.875N is shown in Fig. 5, with the 4f shell of Er being dominant and the Ga 4p shell overlapping with the N 5p shell in the valence band. Conversely, the 4p, 5p and 4f shell overlap in the conduction band.
3.2 Optical properties
The dielectric function describes the linear response of a material to a certain electromagnetic radiation wavelength or photon energy, which relates to the interaction of photons with electrons. Other optical properties can be derived from the complex dielectric function [26]. The following study is carried out using the formalism of Ehrenreich and Cohen, where the complex dielectric function can be written as
where
and
The absorption coefficient α (E) is given by
where
The most important property of a quantum well (QW) is the absorption coefficient, which can be written as
where
where i and j are the initial and final states and f FD is the Fermi-Dirac distribution function. For two consecutive states, Eq. (9) may be written as:
and Eq. (10) can be put into the from
Here n s is sheet charge density and f 21 defines oscillator strength from the first to the second state. The total absorption coefficient of QW is the sum of confined states α w and free states continuum α b approximated by the barrier absorption coefficient given as follows [27, 28]:
This parameter is calculated by combining two numerical techniques; the first describes the optical properties for both materials (ErN, Er0.125Ga0.875N) using the Wien2k package with GGAmBj+ U including a spin-orbit coupling effect, and the second consists in optical properties of QW [29, 27]. Figure 6a) shows the results of the absorbtion coefficient; we noted increasing absorption trends of ErN and Er0.125Ga0.875N while changes in absorption during energy range 0-14 eV. For ErN, the absorption begins at a slightly lower energy, 0.8 eV (1550 nm). It is worth noting that absorption for Er0.125Ga0.875N begins at 3.4 eV (365 nm), which covers a large portion of the solar spectrum. The variation of the optical conductivity is shown in Fig. 6d), where begins to increase and arrives at a maximum of at 2 eV for ErN and 8 eV in Er0.125Ga0.875N for both (xx) and (zz) directions. The evolution of the refractive index and extinction coefficient are shown in Fig. 7. We note that the static refractive index of ErN is 2.3; it begins to increase until reaches its maximum at 2.8 and for Er0.125Ga0.875N, the static refractive indices are 2.9 and 2.4, it shows an increase until it reaches its maximum at 4 and 3.4 for (xx) and (zz) directions. Thus, the extinction coefficient starts to increase from a threshold equal to 2.6 eV for ErN and 3.0 eV for ErGaN in (xx) and (zz) directions.
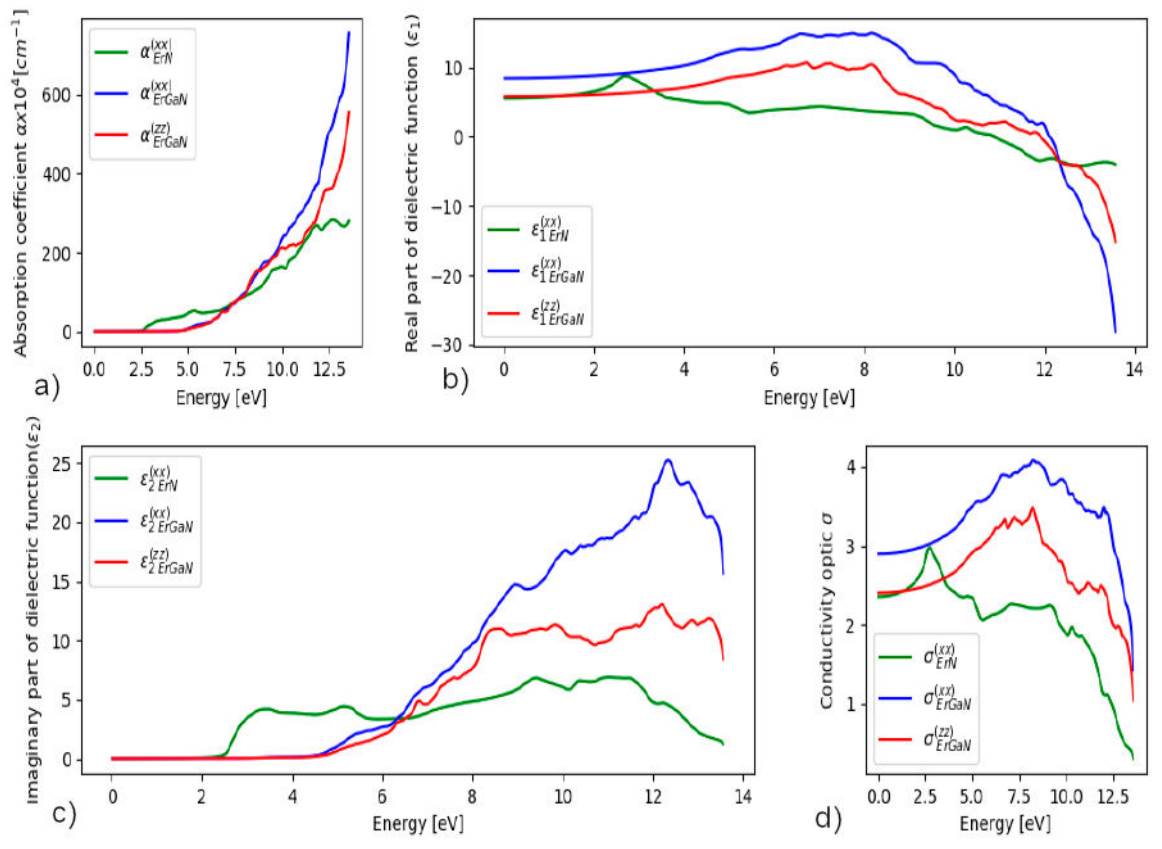
Figure 6 Optical properties: a) absorption coefficient, b) Real part(
3.3 Transport properties
The effectiveness of a material for TE applications is determined by the dimensionless figure of merit,
The electrical conductivity as a function of chemical potential at three constant temperatures (250,300,350) K is shown in Fig. 8, where it is clear that
4 Conclusion
We have studied materials involved in constructing QW of Er0.125Ga0.875N/ErN by ab-initio calculation using DFT theory. The obtained results of the electronic properties show clearly ErN to be a semiconductor with an indirect band gap at 0.79 eV and that Er0.125Ga0.875N presents an indirect band gap at 3.38 eV, using GGA+U approaches, which is in good agreement with other calculations. This indirect band gap was found to improve carrier extractions and lead to improved performance of these properties. The real and imaginary parts of the dielectric function and the optical coefficients were determined. Transport properties of Er0.125Ga0.875N and ErN have been investigated by employing the Boltzman theory implemented in the BoltzTrap code, the electrical conductivity, Seebek coefficient, electronic thermal conductivity, and electronic power factor have been determined; their values show that these materials could be potential candidates for energy conversion. The quantized energy levels present in a quantum well, which can be tuned, provide an opportunity to increase the limited efficiency of solar cells.











 nueva página del texto (beta)
nueva página del texto (beta)