1. Introduction
In broad terms, soft matter exists as a junction between liquid and solid phases of matter. Enhanced sensitivity to weak external stimuli has paved the way in applying soft materials to the development of new technologies and devices, as well as in uncovering functional design behaviors. For instance, the presence of competing interactions between different components prompts a sharp response in material susceptibilities [1] even when system conditions change only subtlety. Common examples of these types of materials include colloids, polymers, surfactants, liquid crystals (LCs), and dispersions [2]. A remarkable property resulting from the interplay of repulsive and attractive interactions is the ability of soft matter to self-organize, with structural order persisting to relatively large length scales (from angstroms to microns) [3,4]. Micelles, vesicles, fibers, gels, microemulsions, and membranes are a few examples illustrating the attainable spectrum of materials and length scales.
A special class of soft matter systems is found in LCs: these molecular systems possess an underlying anisotropic molecular core which allows for fluidity of the liquid phase to exist in concert with long-range order characteristic of solid materials. This gives LCs the ability to display a variety of mesophases tunable via thermodynamic state points or solvent conditions. More importantly, LCs are highly sensitive to changes in their local environment, a trait which has been the inspiration behind a host of sensors and optoelectronic technologies.
The ability of LCs to straddle solid and liquid properties provides a fertile ground for molecular organization. In general, a pure mesogenic sample will orient along a preferred direction given an appropriate thermodynamic state point. This behavior leads to a so-called bulk nematic director: this order will persist, subject to small thermal fluctuations, provided a compatible thermodynamic state point is maintained. However, this directional tendency is disrupted in the presence of molecular inclusions, a confining boundary (which imposes a local field), or an externally applied field. This break in symmetry is manifested in the LC sample through disclinations or topological defects. A variety of topological defects can be produced depending on the nature of the LC, the type of inclusions, and the thermodynamic state point.
Topological defects brought on by colloidal inclusions will manifest themselves by surrounding the guest particles. These defects, in turn, can mutually “communicate” in a way that they can “escort” colloidal particles into arrangements yielding self-organized structures. This approach has led the way into a shift in paradigm, where the solvent is directly involved in the self-assembly process [5-9]. Hence, the solvent provides an added layer of control that can widen the gamut of attainable targets [10-13]. For instance, colloid-induced disclinations can mutually couple with one another to yield dimers [14-25], wires (i.e., chains) [8,15,22,26-31], and arrays [8,18-21,23-25,30,32,33]. The variety of metamaterials can be extended by recruiting solvents to function as active contributors in the self-assembly process.
In this review, we highlight research from our group involving computer simulations of LCs, with an eye on mixtures. Because our studies make use primarily of Molecular Dynamics (MD) simulations (in both canonical NVT or isothermal-isobaric NPT ensembles), it is possible to probe not only the time evolution of the mesogenic solvent, but also to capture the relaxation timescales associated with molecular events leading to symmetry-breaking phenomena. Both calamitic and discotic mesogens are considered in this work. After reviewing some essential features of LC phenomenology, we summarize the formalism of the coarse-grained representation of the Gay-Berne model. We then discuss extensions of the model when treating binary (symmetric) mixtures, nematic colloids, nanodroplets, and confined systems. The ability of these systems to convey structural information to other units through pattern formation highlights their relevance in hierarchical molecular self-organization.
2. Liquid crystal classification
The discovery of LCs [34] has ushered an important facet of soft matter systems: the volume of experimental and theoretical work is nothing short of impressive [1]. LCs have stimulated a wide range of device applications. Liquid crystal displays (LCDs) represent one of the many tangible applications of liquid crystalline phases. Due to their ability to “bridge” solid and liquid phases, LCs exhibit intermediate phases not accessible in ordinary, bulk systems. Although LCs flow like liquids, they also possess some characteristic properties of a crystalline solid within certain thermodynamic state points. The molecules making up these materials with unusual phase behavior are denoted mesogens: the various phases they present are called mesophases.
For a fruitful discussion on the properties of LCs, it is important to have a basic understanding of their classification and mesophase stability. A simplified classification scheme is provided in Fig. 1. The stability of mesophases can be outlined according to an underlying parameter describing the system: for example, the mesophases identified in thermotropic systems are differentiated through temperature. The mesophases observed in lyotropic systems are differentiated through concentration and temperature. These latter systems encompass a large class of solutions, including aqueous solutions of the tobacco mosaic virus [35-37]. A variety of mesophases exist, including nematic, cholesteric, smectic, and ferroelectric [38], each with specific physical properties.
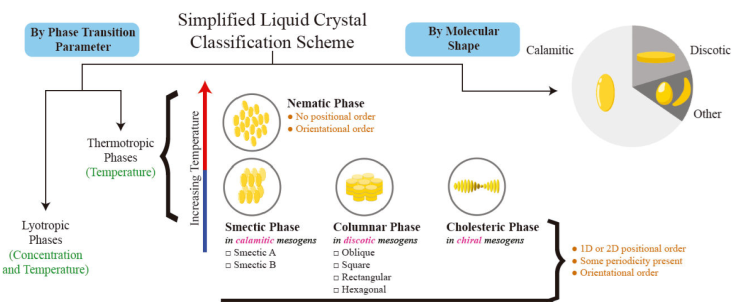
Figure 1 A simplified classification scheme of liquid crystal systems, based on phase transition parameter and molecular shape. The thermotropic case is further illustrated in the diagram, outlining features for the ordered phases and the type of mesogen that produces them. The classification by molecular shape qualitatively highlights the research that has been devoted to each class by means of a pie chart: the most extensively studied molecular shape is the calamitic mesogen.
The physics of LCs depends on the structure and chemical composition of the mesogenic molecule. Most LCs are derived from benzene, and include aromatic rings in their chemical structure, such as saturated cyclohexane or unsaturated phenyl, biphenyl, and terphenyl in various combinations [38]. According to their molecular form, mesogens are classified broadly as being calamitic (prolate) or discotic (oblate). Calamitic mesogens tend to form smectic mesophases, while discotic mesogens self-organize into columnar mesophases. The smectic phase exhibits two-dimensional charge transport while the columns of discotic mesogens exhibit one-dimensional charge transport [39].
Other mesophases are attainable with molecules possessing a more complex shape, such as bent- or pear-like mesogens [40]. A feature common to all these systems is their underlying anisotropic shape, which promotes the spontaneous ordering of molecules [41] through entropic constraints. Molecular self-organization occurring in LC mesophases exemplifies a phase transition of entropic origin. As shown by Onsager [35,36], the isotropicnematic transition in infinitely long and thin rods can be explained as the competition between translational and rotational entropy.
Mesophases are classified according to the distribution of orientations ê (i.e., the set of unit molecular vectors e) and positions r of the LC molecules. For instance, the nematic phase presents long-range orientational order [37] in which LC molecules are oriented along a preferred direction denoted the nematic director
where ⊗ denotes the tensor product, I is the identity matrix, and N is the number of mesogens contained in the ensemble. The diagonalization yields S
2 = λmax as the largest eigen-value and the associated normalized eigenvector corresponds to
3. Computer simulations of liquid crystals
3.1. The Gay-Berne mesogenic model
Computer simulations have played a key role in understanding the way molecular features give rise to the complex phase behavior of LC systems, in part due to the amount of detail attainable from the data. Even on a coarse-grain level, computational models provide unique insight into phase order and stability which help inform the development of new experiments or theories. When it comes to mesogenic models, the Gay-Berne (GB) interaction potential is used widely to study thermotropic phase transitions in LCs [42,43], and because of its continuous (as opposed to discrete) representation, it can be implemented in conventional MD routines.
The GB interaction potential, coupled with computer simulations, describes the origin of short- and long-range order, phase stability, interfacial properties, and dynamic behavior arising from the microscopic structure of a mesogen. A key feature of the GB potential is the ability to account for the anisotropy in attractive and repulsive interactions by generalizing the Lennard-Jones (LJ) potential: the attractive and repulsive contributions scale as r ij -6 and r ij -12 , respectively, where r ij is the magnitude of the center-to-center vector r ij . More specifically, r ij = ǀr ij ǀ, and r ij = r i - r j , in which r i and r j are the position vectors of the ith and jth mesogens, respectively. The interaction further depends on ê i and ê j , which are the molecular orientations of the ith and jth mesogens, respectively. Each mesogen is represented by either a prolate or an oblate ellipsoid. The orientation of each mesogen at any instant in time is defined by a unit vector: in prolate mesogens, the unit vector ê coincides with the molecular (major) axis, whereas for oblate mesogens, ê is normal to the oblate face. The mesogen-mesogen potential is given by
where the energy scale is tempered by 𝜖(ê i , ê j , ȓ ij ) and the length scale of interaction is captured through Ξ(ê i , ê j , r ij ). Two types of anisotropy are present in U mm(ê i , ê j , r ij ): one is related to molecular shape and the other arises from chemical signatures (i.e., the energy of interaction varies according to different spatial arrangements). Both types of anisotropy are accounted for via 𝜖(ê i , ê j , ȓ ij ) and Ξ( ê i , ê j , r ij ).
To define the anisotropic terms, a fully specified function of a general variable ω is introduced,
where c i = ê i · ȓ ij , c j = ê j · ȓ ij , c ij = ê i · ê j and ȓ ij = r ij /ǀr ij ǀ is the unit (center-to-center) separation vector. Now,
where σ min is the shortest contact distance between two mesogens. Specializing this to calamitic LCs, σ min is the side-side [width, thickness] diameter σ s, whereas the end-end [length] diameter is σ e. For discotic LCs, σ min is the face-face [width, thickness] diameter σ f, whereas the end-end [length] diameter is σ e. Moreover,
where σ 0 is the length scale corresponding to the separation between mesogens when their molecular orientations are orthogonal to the intermolecular vector r ij (i.e., c i = c j = 0). Outside of this limit configuration, the relative spatial arrangement of mesogens tempers the value of σ 0 via Eq. (3) and
which accounts for molecular anisotropy through the aspect ratio κ. For calamitic systems, κ = σ e =σ s > 1, whereas for discotic systems, κ = σ f =σ e < 1.
The anisotropy in energy scales due to chemical features is introduced effectively through
where 𝜖0 is the potential energy well depth for two mesogens orthogonal to one another (i.e., cross configuration) and to the center-to-center vector (i.e., c i = c j = c ij = 0). In addition, 𝜈 and 𝜇 control the contribution of the two dimensionless energy factors, 𝜖1(ê i , ê j ) and 𝜖1(ê i , ê j , ȓ ij ). In particular,
controls the parallel alignment of mesogens. The second term,
is defined in terms of Eq. (3), where
depends on the energy anisotropy parameter 𝜅 ’ . In an analogous manner to the molecular aspect ratio, for calamitic systems, 𝜅 ’ = 𝜖 s =𝜖 e > 1 favors the formation of smectic phases (𝜖 s being the energy well depth for the side-side configuration and 𝜖 e the well depth for the end-end configuration). For discotics, κ’ = 𝜖f/𝜖e < 1 favors the formation of columnar phases (𝜖f being the energy well depth for the face-face configuration and 𝜖e the well depth for the end-end configuration). Physically, κ’ describes the anisotropy in charge distribution on the mesogenic molecule. When κ’ = 1, the charge distribution is homogeneous and there is no preferred interaction. For cases where κ’ ≠ 1, a nonuniform charge distribution leads to the characteristic mesophases previously discussed.
By convention, different parameterizations are summarized by listing them in the form GB(κ, κ’, µ, ν), each parameter defining anisotropic contributions to the interaction energy. Although many GB parameterizations are possible, only a limited number has been studied [44-47]. Computer simulations [43,46,48-50] and theoretical studies [51,52] have focused on several aspects of LC phase behavior using the GB representation, which reproduces with sufficient accuracy much of the associated phenomenology [53]. A frequently cited parameterization for a thermotropic calamitic is GB(3.0, 5.0, 2, 1), originally constructed to mimic anisotropic interactions in an equivalent linear-site LJ potential [53], though this system is not unique [46,47].
The GB(4.4, 20.0, 1.0, 1.0) parameterization is inspired by a real chemical system to model the mesogenic domain of p-terphenyl. Studies have focused on phase behavior [46], pair distribution functions [46], rotational dynamics [54], structure of various phases, and calculations of X-ray scattering patterns [55] for this parameterization. On the other hand, many experimental studies have focused on characterizing the general behavior of the 4-cyano-40-pentylbiphenyl (5CB) mesogen. The parameterization most studied and most similar to the 5CB mesogen is GB(3.0, 5.0, 2, 1): the interaction potential is shown in Fig. 2.
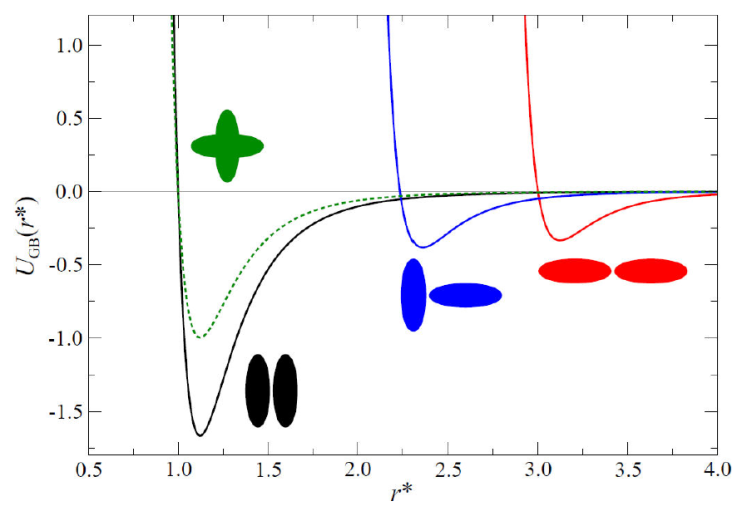
Figure 2 The Gay-Berne interaction potential U GB (r) for characteristic configurations of the calamitic (prolate) mesogen system, GB(3.0, 5.0, 2, 1). Shown are side-side (black line), cross (green dotted line), tee (blue line), and end-end (red line) arrangements. In practice, the potential takes all configurations between the side side and end-end limiting cases. Molecular schematics are shown near each well (by color) for easy identification. The intermesogen separation has been normalized such that r * = r / σ 0.
In this review, the GB(3.0, 5.0, 2, 1) and GB(4.4, 20.0, 1, 1) mesogens were selected to model calamitics: not only are these models the basis of previous work, but they capture LC phases to varying extents. For example, the GB(3.0, 5.0, 2, 1) parameterization cannot describe a smectic A phase, while the smectic B phase obtained with this model is purportedly a solid phase [50]. Prior simulation studies suggest that the smectic B phase is not very sensitive to GB parameterizations, but the formation of the smectic A phase requires a sufficiently large aspect ratio κ [44,46,56,57]. As κ increases, so does the smectic A region of the phase diagram; however, the region is bounded at high and low temperatures [56]. The GB(4.4, 20.0, 1, 1) parameterization was employed to study translational self-diffusion in nematic, smectic A, and smectic B phases [46,58].
A generalization of the GB potential proposed by Cleaver and coworkers [59] considers interactions between molecular units with different aspect ratio: this approach is equivalent to taking two identical ellipsoidal units of cylindrical symmetry, scaled by length and width factors. These extra factors have no restrictions and enable the modeling of interactions between calamitic mesogens with small or large variations in length, between calamitic and discotic LCs, or between mesogenic and spherical particles. This construct allows one to model a variety of LC mixtures via computer simulations.
3.2. Liquid crystal mixtures
Current technological applications of LCs primarily involve multi-component mixtures [60,61]. When it comes to formulating LC mixtures with specific characteristics, the task is more a black-box process rather than a science at all. In many cases, devices that use LC-based properties are mixtures of at least twenty components. Despite this highly involved approach, desired features are achieved only with great difficulty. If equivalent features can be obtained with a mixture of only a few components, it would be consequential in terms of chemical synthesis and technological implementation. To this end, a good understanding of the relationship between molecular characteristics and macroscopic properties (e.g., phase stability, elastic constants, dielectric constants, viscosity, etc.) becomes necessary. Many pure LCs have a narrow temperature region in which the nematic phase is stable. For instance, the nematic region is sought after in practical applications for temperature ranges as wide as possible so that optoelectronic devices remain stable, even under extreme operating conditions. Therefore, it is desirable to have a platform whereby combining different materials still preserves the properties of their corresponding pure states. When compared to their pure counterparts, mixtures have richer phase behavior.
Until recently, simulations with the GB potential had been restricted to single-component systems. The main reason for this limitation lies in the original form of the GB potential, which can only describe interactions between molecules of the same type. As noted earlier in the literature [62,63], using the GB potential with Lorentz-Berthelot combination rules as a first approximation is not entirely appropriate for anisotropic molecules. More specifically, the so-called “mixing rules” do not differentiate between tee configurations involving different mesogenic cores, i.e., AB interactions are not the same as BA interactions. This discrepancy is not too problematic for molecules of similar size, where parallel molecular configurations are dominant over the tee configuration. Therefore, the GB potential must be modified to consider interactions between molecules of different geometric shapes (e.g., prolate versus oblate) in multicomponent systems. Such a formulation was carried out by Cleaver [59], in which the interactions between particles of different geometry were taken into account. The interaction potential for a binary LC system is shown in Fig. 3.
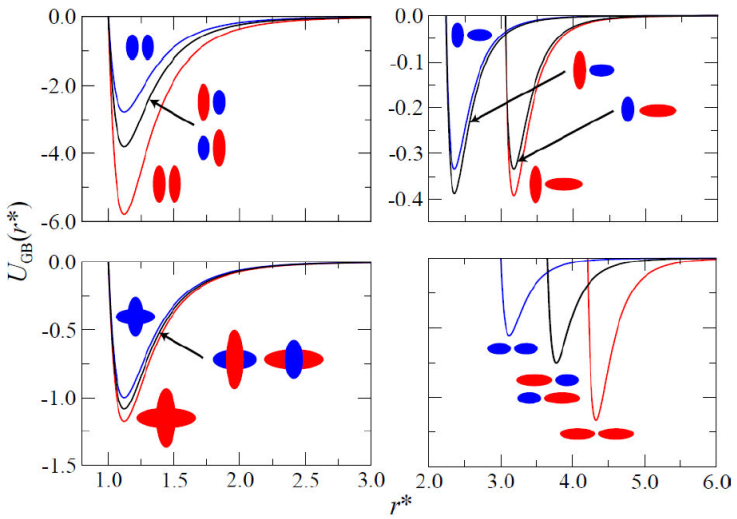
Figure 3 The interaction potential for a symmetric binary mixture. Curves are colored to match molecular schematics, except that black curves correspond to mixed (i.e., AB and BA) cases. The intermesogen separation has been normalized as in Fig. 2.
We report here unpublished results from our group obtained for an equimolar binary mixture using the generalized GB potential. Two cases of the aspect ratio κ were considered in this study: 4.2:1.0 and 3.0:1.0 for A and B species, respectively. Studies were carried out in the NPT ensemble using MD simulations. Moreover, the modified exponents μ = 1 and ν = 2 were used in the generalized GB potential. In Fig. 4, we present the behavior of the nematic order parameter S 2 as a function of temperature for the mixture and the corresponding pure components. Temperature ranges in which different orientational phases are stable in the system can be easily identified by inspecting the response in S 2. We invite the reader to review our prior work [14,64-68] for examples illustrating the use of reduced variables to map mesogenic models to experimental systems; additionally, the reader can take note of typical simulation run parameters and the MD methodology used to obtain equilibrium data.
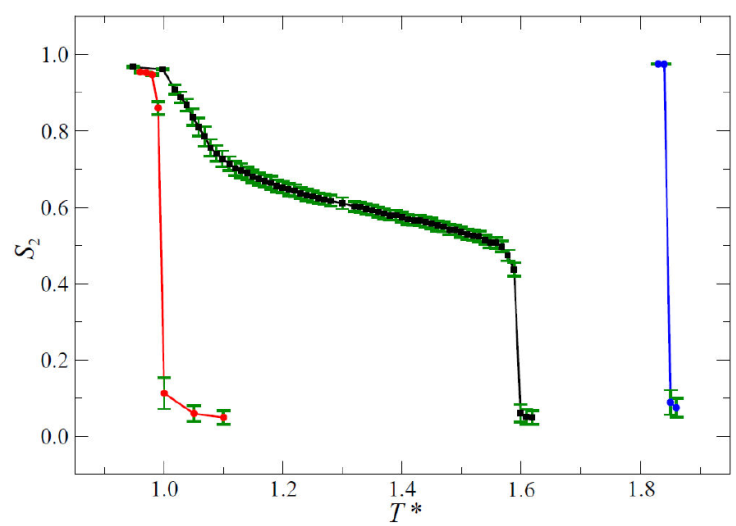
Figure 4 Temperature dependence of the Maier-Saupe S 2 order parameter for a 50:50 (symmetrical) mixture of calamitic mesogens (black squares). The mixture consists of mesogens with 𝜅 = 4.2 (blue circles, pure A sample) and 𝜅 = 3.0 (red circles, pure B sample). Lines through the symbols serve as a guide to the eye. Error bars are shown as green riser lines.
As 𝜅 of a pure sample increases, so does the transition temperature associated with ordered phases, a feature gleaned from Fig. 4. This is a well-known observation [56] rationalized by the fact that the attractive part of the GB potential deepens (becoming more favorable energetically) as 𝜅 increases. Because we study equimolar mixtures, the temperature range in which ordered phases appear is located between those of the pure species. The most interesting behavior in mixtures, however, is that the temperature range in which ordered phases are stable is significantly widened when compared to the temperature range of the pure components, in agreement with experiments [69]. This potentially broadens LC-based applications by alleviating the need for stringent temperature requirements to attain desirable mesophases.
3.3. Nematic colloids
Nematic colloids are systems in which guest colloids are suspended or immersed in an oriented host mesogenic solvent. Due to the anisotropy of elastic interactions, these systems produce topological defects with captivating self-organizing properties [13,70-72]. A topological defect will emerge in a region where a discontinuity occurs in the bulk orientation of the mesogenic fluid [1,73]. Experimental techniques, such as optical tweezers, have enabled the observation of self-assembled structures in these systems [8,74,75]. Topological defects and their associated thermodynamic state points are relevant in many technologies, such as flexible screens [76], photonic displays [77], and bistable cholesteric screens [78]. Increased interest in the ability to control defects within LC media lies in advancing strategies for molecular self-organization and designed materials. Topological defects cooperatively provide a patterning platform to direct colloidal assembly into specific geometries through elastic interactions [6,79-83].
Structural scaffolds are possible using nematic colloids through the colloid-mesogen (CM) interaction. Although the energy contribution can be attractive or repulsive, elastic defects appear in either scenario. The colloid acts as an obstacle that interrupts the orientational order of the nematic fluid when the CM interaction is repulsive. On the other hand, two limiting anchoring modes (planar and homeotropic) are possible when the CM interaction is attractive, thus generating a characteristic defect. As a result, the dynamical properties of this complex system depend on the type of anchoring.
The orientational order in a nematic fluid corresponds to a vector field of mesogens making up the LC medium. More specifically, the ensemble of molecular orientations in the mesogenic fluid creates the nematic field. Simulations and experiments show that the attractive CM interaction in the vicinity and on the surface of a colloid has a stronger effect than the local energy of the nematic field. This causes the mesogenic cores to change their orientation near the colloid and break the rotational invariance of the medium. It is important to note that, unlike a conventional vector field, the pointing direction of the nematic director is indistinguishable, i.e.,
Both system temperature and size of colloidal particles affect the type of topological defects observed. For instance, homeotropic anchoring can lead to a hyperbolic hedgehog-like defect or a Saturn ring around the colloid [74,84]. On the other hand, planar anchoring leads to the distortion of the nematic phase at two points on the colloidal surface, along the direction of the nematic field: this defect is commonly known as boojums. These cases are summarized in Fig. 5. Interactions between colloids and mesogenic particles leads to the formation of defects in the vicinity of each colloid. The self-assembly of guest colloidal particles in a host mesogenic solvent results from energy minimization of the system by reducing the volume in which orientational disruptions (i.e., defects) occur. Studies of suspended particles in nematic LCs show that the interaction energy involved in the assembly of micrometer-sized particles is of the order of several hundred k B T, where k B is the Boltzmann constant and T is the absolute temperature. Consequently, self-assembled structures formed through the interaction between topological defects are highly stable [8,85,86].
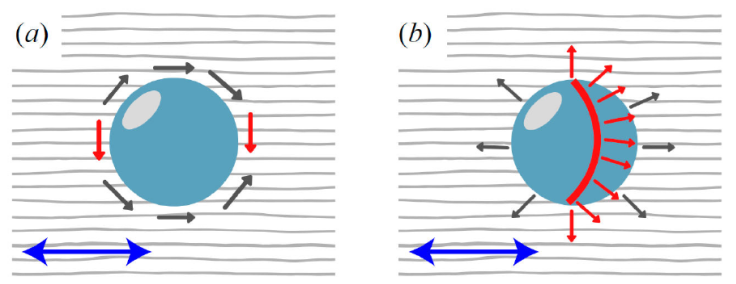
Figure 5 Colloidal inclusions immersed in a liquid-crystalline solvent
induce topological defects. The defect observed (red) depends on how
the mesogens (represented by their molecular orientation vectors as
single-headed arrows) anchor onto the colloid surface. a) Planar
anchoring leads to coupled point defects known as
boojums. b) Homeotropic anchoring leads to an
annular defect known as the Saturn ring. Bulk
orientational order is shown by the gray streaks in the background.
The blue double-headed arrow highlights the equivalence of the
system for the nematic director, i.e.,
3.4. Modeling colloidal inclusions in a mesogenic solvent
To describe the interaction between colloidal inclusions and mesogenic units, we use a modification of the LJ potential developed by Cleaver and Antypov [87]. Molecular anisotropy is introduced via contributions analogous to those described by Eqs. (5) and (7). As before, the shape anisotropy takes into account the shape and size of interacting particles, the orientations of mesogenic units, and the interparticle distances. The energy anisotropy is responsible for favoring certain configurations by promoting different anchoring types through differences in potential well depths.
The evolution of solid, rigid colloids immersed in a fluid of n mesogens with coordinates {r} 1,n = {r1(t), r2(t),…,r n (t)} and orientations {ê} 1;n = {ê 1(t), ê 2(t),…, ê n (t)} is captured by the total interaction energy,
where mesogen-mesogen contributions are accounted for by U mm, colloid-mesogen contributions by U cm, and colloid-colloid contributions by U cc. Note that U mm is a function of all positions and orientations of the n mesogens. On the other hand, U cm depends on the positions and orientations of the mesogens, as well as the positions of the colloidal inclusions.
To represent this system mathematically, we use Eq. (2) for U mm. For U cm, the extended LJ representation for spherical and anisotropic particles is used [88]:
and d ij = r ij - R is the relative separation between the surface of the colloid of radius R located at position r i and the center of mass of a mesogen at position r j with orientation ê j . Now, r ij = ǀr i - r j ǀ is the relative distance between the centers of mass of the two interacting particles. The distance ζ(ê j , ȓ ij ) is analogous to Ξ(ê i , ê j , r ij ) in Eq. (4).
Anisotropic contributions are taken into account through energy and length scale functions defined as
and
with
and
where
is the ratio of well depths between homeotropic (𝜖 h) and planar (𝜖 p) anchoring. The effect of varying 𝜅’’ is as follows: if 𝜅’’ = 1, both planar and homeotropic arrangements are equally favored. Homeotropic anchoring is favored when 𝜅’’ > 1, whereas planar anchoring is favored when 𝜅’’ < 1. The latter case is depicted in Fig. 6; the potential varies as the mesogen changes its orientation relative to the colloid.
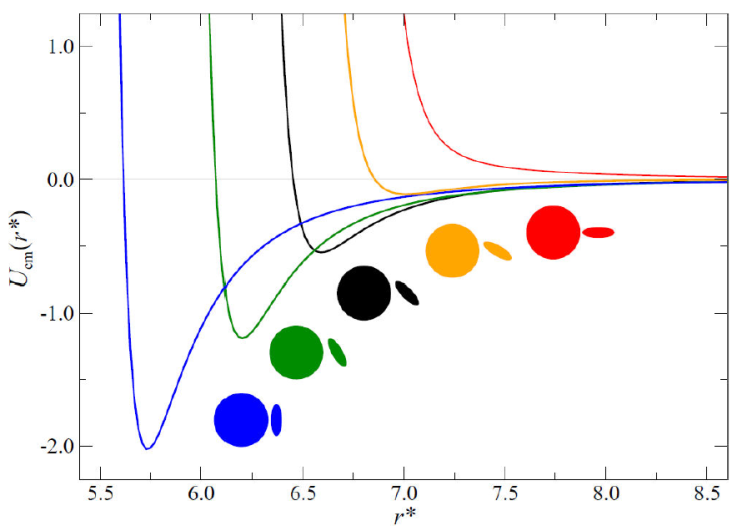
Figure 6 The colloid-mesogen interaction potential U cm (r) when planar anchoring is favored (𝜅’’ < 1). Highlighted are a few cases of the relative orientation between the mesogen and the colloid. In practice, the interaction is accounted for through a continuous sweep based on the instantaneous colloid-mesogen orientation. Length scales have been normalized as in Fig. 2.
The contribution for U cc is accounted for in our model through a soft, repulsive contribution (refer to our previously published study for details on the mathematical form of this term [14]). By suppressing attractions from a colloid-colloid potential well, it becomes possible to uncover effective interactions mediated solely by topological defects.
3.5. Topological defects due to colloidal inclusions
Many nematic colloidal systems have been investigated with the model presented in Sec. 3.4. The most studied example consists of a colloid with homeotropic anchoring in a matrix of calamitic mesogens. Experimental studies have characterized the general behavior of the 5CB mesogen, and most computational work has resorted to the GB(3.0, 5.0, 2, 1) parameterization for this purpose (as previously discussed in Sec. 3.1).
Topological defects on colloidal inclusions are illustrated in Figs. 7 and 8, where a cross-section of a simulation snap-shot is shown alongside a color map of the local order parameter in the same plane, for homeotropic and planar anchoring. The calamitic GB(3.0, 5.0, 2, 1) and discotic GB(0.345, 0.2, 1, 2) systems [14,64] are shown for the two limiting anchoring cases: planar (top panels) and homeotropic (bottom panels). The radius of the colloid was chosen to span two to three mesogenic units (along the longest mesoden dimension). In both cases, mesogens adopt an orientation consistent with the bulk immediately beyond the mesogen shell on the colloid surface. The local order parameter S 2;loc in the bulk ranges between 0.5 to 0.8, corresponding to the nematic phase. The defects observed near the colloid surface depend on the type of anchoring: planar anchoring leads to boojums and homeotropic anchoring leads to a Saturn ring. The qualitative equivalence of defects for each type of anchoring stems from the fact that similar orientational distortions of the medium arise on the colloid surface.
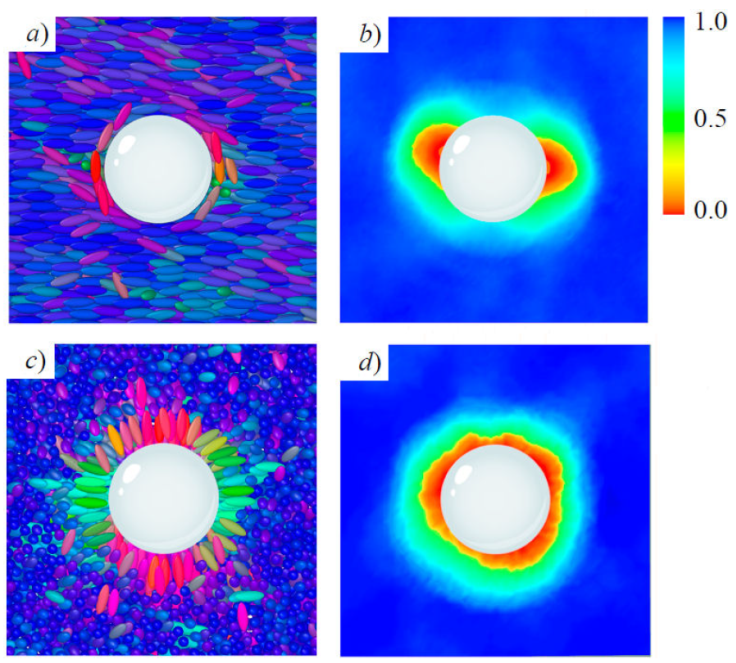
Figure 7 Equilibrium configurations of a colloidal inclusion (white sphere) immersed in the GB(3.0, 5.0, 2, 1) calamitic solvent. Mesogen colors denote orientation. Planar anchoring leads to a boojum: a) cross-section snapshot, and b) color map of the local S 2 parameter. Homeotropic anchoring leads to a Saturn ring: c) as in a) and d) as in b), respectively. Note that in c), the major axis of most mesogens in bulk regions points at the reader. The color bar characterizes S 2 within a local region on the color map.
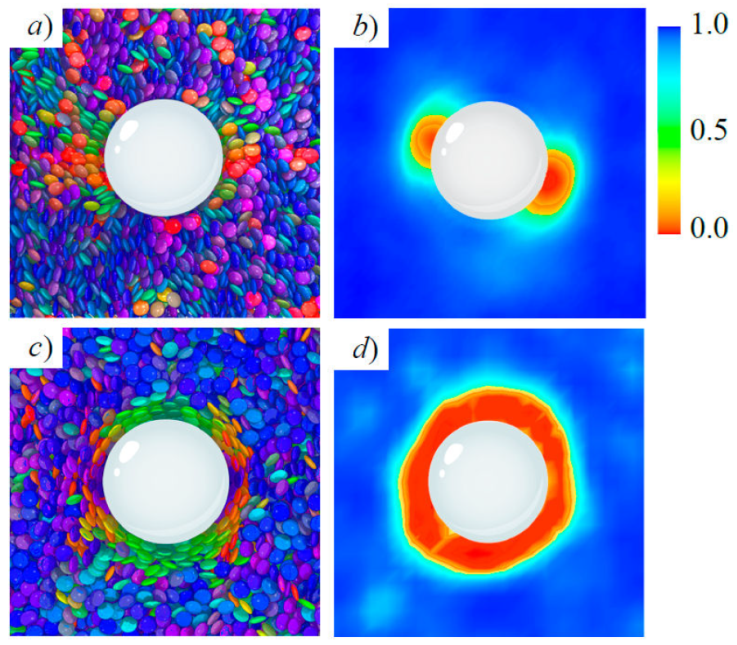
Figure 8 As in Fig. 7, but for the GB(0.345, 0.2, 2, 1) discotic solvent. Planar anchoring leads to a boojum [Panels a) and b)], whereas homeotropic anchoring leads to a Saturn ring [Panels c) and d)].
Computational studies show that colloidal diffusion has a marked dependence on anchoring. For example, homeotropic anchoring produces a larger hydrodynamic radius (i.e., the mesogens extend further out from the colloid surface), which in turn reduces the diffusion of colloids when compared to parallel or no anchoring [64]. Thus, “programmed anchoring” can modulate system dynamics without requiring a change in colloidal particle size. This avenue is of particular interest in cases where spatial requirements must be satisfied in confined systems, such as those encountered in LC-based devices.
3.6. Interactions mediated by topological defects
This section focuses on the interaction between topological defects on guest colloidal inclusions immersed in a host mesogenic solvent. Specifically, we probe how topological defects “communicate” within the medium to induce colloidal arrangements. We previously reported results for a variety of system conditions [14]. Here, we focus on the system in which the distance between colloidal surfaces R 12 is approximately 1.7(±0.2)σ e.
The ability of defects to interact with one another leads to solvent-mediated
self-organization of an ensemble of colloids. Several factors influence the
defect type observed between colloids in the nematic solvent. One of these
factors is the relative arrangement of colloids within the nematic field. Let
R12 be the vector joining the centers of mass of two
colloids. The defects observed will depend on the angle between the nematic
director
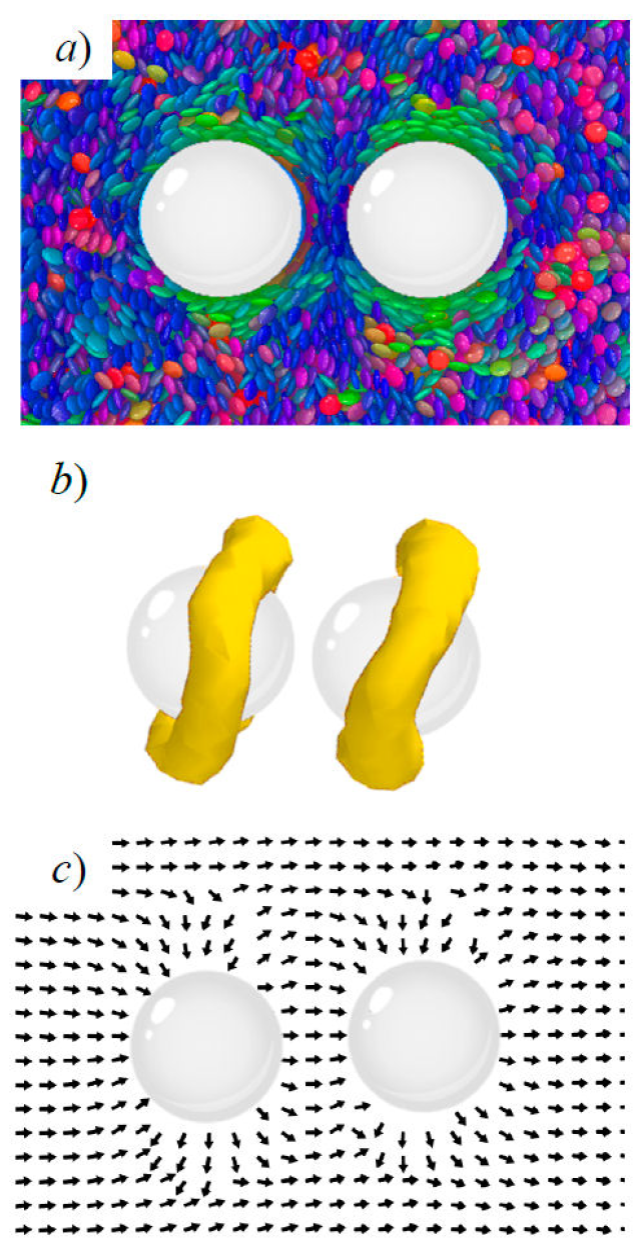
Figure 9 A pair of colloids immersed in the GB(0.345, 0.2, 2, 1) discotic solvent. Mesogens are colored according to orientation. Shown is homeotropic anchoring, with the intercolloid vector parallel to the nematic director: a) a simulation snapshot, b) surface view of the topological defect, and c) the local nematic director field.
As mentioned previously, LC solvent-mediated colloidal structures are driven to minimize
energy penalties in the system. The Saturn ring formation for the parallel
arrangement between
When
The previous discussion on the interaction of topological defects underscores the importance that MD simulations have in clarifying their stability and temporal evolution in LC systems. For example, the ability to distinguish features which are dynamically stable (albeit fluctuating) from those that have a short relaxation time is useful in strategically choosing LC systems destined for assembled superstructures. The elastic interactions can be measured and then used to identify candidate systems with adequate chemical interactions that satisfy required spatial and strength thresholds.
3.7. Topological Defects Under Flow
The study of rheological properties and the effects of flow on mesophase structure and morphology is involved because such properties not only depend on molecular form and size, but also on temperature and direction relative to the phase director. These properties are of prime interest because many LC states of matter are coupled with rheological and optical properties characteristic of liquid and/or crystalline phases. Thus, although they possess the ability to flow like ordinary liquids, LCs remain sufficiently structured while doing so, to the extent that X-ray diffraction and polarized light transmission are attainable experimental probes. Polarized optical microscopy enables the identification of mesophases present in an LC sample [100-110].
To address systems under flow, we envision a colloidal particle subjected to a fluidic stream of the mesogenic solvent moving at a flow speed v. A colloidal particle of radius R is submerged in a rectangular stream with a square cross-section. This configuration allows to trace how topological defects respond as flow speed varies. The extent to which the director field is distorted under flow is commonly quantified by the dimensionless Ericksen number, E r = γvR/K, which defines the ratio of the viscous force prompted by the rotational viscosity γ of the LC medium (as γv/R 2) to the static force arising from the medium through the Frank elastic constant K (as K/R 3) [111-113].
Qualitatively, there are three regimes for E r that can be used to classify the extent of defect distortions. Consider a colloidal particle and its associated topological defect. For sufficiently low values of E r (i.e., those arising from low v), defects will preserve their position and shape. As E r increases, defects will be displaced from their average position on colloidal particles. Now, if E r is sufficiently large, defects will detach completely from colloidal particles and vanish altogether [114]. Computational and theoretical studies on calamitic systems show that for sufficiently large E r, defects are displaced downstream of solvent flow [115-120], although this does not appear to apply in all cases [85,111,121].
In this review, we focus on exploring the behavior of topological defects under flow but for a discotic solvent, and more specifically, the GB(0.345, 0.2, 1, 2) discogen. We summarize our new findings in Fig. 11 for planar and homeotropic anchoring for moderate E r. Consistent with previous results for calamitic systems [21,115,116,118,121-125], topological defects are displaced downstream. At first glance, such a displacement is physically intuitive. However, upstream defect displacements have also been observed under specific conditions [85,111,121], suggesting that such phenomenology is more involved. A striking observation for our discotic system is that the boojum defect (which would be colinear with solvent flow) distorts into a trailing stomal defect [refer to Panel (a) in Fig. 11]. This is a stark departure from the conventional lobal displacement of boojum defects observed in calamitic systems [115,116]. The downstream displacement of the Saturn ring is consistent with prior findings [115,116]. A future publication by the authors of this review will focus on a study of similar discotic systems under flow.

Figure 11 The displacement of a topological defect under flow for a colloidal particle (white sphere) immersed in the GB(0.345, 0.2, 1, 2) discotic solvent. Mesogen colors denote orientation. Shown is a snapshot (left panels) and the corresponding visual highlight of the distorted topological defect (right panels) for a) planar and b) homeotropic anchoring. The direction of solvent flow is indicated by the arrow.
Observing the response of anchored LCs and the evolution of topological defects under flow, as pursued in this preliminary study, establishes an important connection between experimental phenomenology and theoretical predictions. However, the quantification of the anchoring force a mesogenic unit experiences on the surface of a colloidal particle remains a challenging experimental feat. Difficulties aside, such force measurements are crucial to the prediction of defect types and aggregate structures in mesogenic suspensions. Additional model systems and flow conditions using MD simulations will be pursued in our group to characterize non-equilibrium forces for shear-induced molecular assembly.
3.8. Liquid crystals and confining substrates
The next area of focus lies in the spatial confinement of LC samples. Under these conditions, the ordering of mesogens is highly sensitive to the interactions at a confining boundary or an interface. For instance, a local disruption in LC order can be driven by a molecular-level perturbation (i.e., a transient temperature change), by the interaction of mesogens with surface molecules, or in response to an externally applied field. A nanoscopic disruption can be magnified via “transmission” of orientational disorder to an observable macroscopic scale. For this reason, changes in LC orientational order caused by the presence of lipids, surfactants, proteins, and viruses [126,127] can be readily detected. Sensors and detectors with nanoscale resolution have been designed using LC-based platforms [128].
Potentially useful mesophases that can “transmit” local orientational perturbations include the isotropic, nematic, smectic, cholesteric, and columnar phases [1]. The ability of LCs to achieve desirable mesophases depends on the shape and aspect ratio of the mesogens. For example, phase diagrams of two LC fluids with parameterizations GB(3.0, 5.0, 1, 2) and GB(2.0, 5.0, 1, 2) exhibit isotropic, nematic, and smectic B phases [65]. The 𝜅 = 3.0 mesogen also displays a smectic A phase: the physical basis for this last observation is that molecular elongation leads to more favorable interactions to support ordered phases at higher temperatures and lower densities when compared to the 𝜅 = 2.0 mesogen.
When confinement is reduced to nearly nanoscale arrangements, the resulting local perturbations are detectable by LC systems due to their high sensitivity. Considering a sample confined between walls, distortions arising at the interface can transmit structural information from the surface toward the bulk. The effectiveness of the transmission will depend on the thermodynamic state point, the type of mesogenic unit, the transmission length scale (i.e., bulk depth), and the strength of the wall-mesogen coupling [65].
In a previous report, we considered the ordering effect of a smooth, structureless wall [65] with planar anchoring only. When the wall-mesogen coupling strength exceeds a thresh-old, fluid stratification near the wall extends toward the bulk region of the slab, an effect that decays with distance for the 𝜅 = 2:0 mesogen [65]. Although stratification is not an important effect in the 𝜅 = 3:0 mesogen, if the wall coupling strength is sufficiently strong, smectization is observed [65]. Additionally, the isotropic-nematic transition shifts to lower temperatures when the wall-mesogen interaction is strong.
Although important insights from theoretical formalisms aid rationalizing certain LC phase behaviors [129-132], the need to suppress density fluctuations and spatial disorder for tractability can lead to difficulties in describing microscopic interactions [133] responsible for interfacial structures [134]. Interfacial forces from the confining wall can drive specific molecular assemblies. These possibilities may be explored directly with computer simulations by relaxing simplifications and using physically relevant interaction potentials.
We extended the confined calamitic model [65] to include microscopic detail for the confining walls. In this enhanced representation, the boundary consists of LJ particles tuned to prompt planar or homeotropic anchoring. An interesting variation is a wall made by mixing homeotropic- and planar-anchoring particles. Here, concentration is an additional parameter so we refer to this as the “concentration-dependent” scenario. All three scenarios are shown in Fig. 12. The concentration-dependent case is important because local domains within the boundary can be followed as the system minimizes its energy given competing anchoring types.
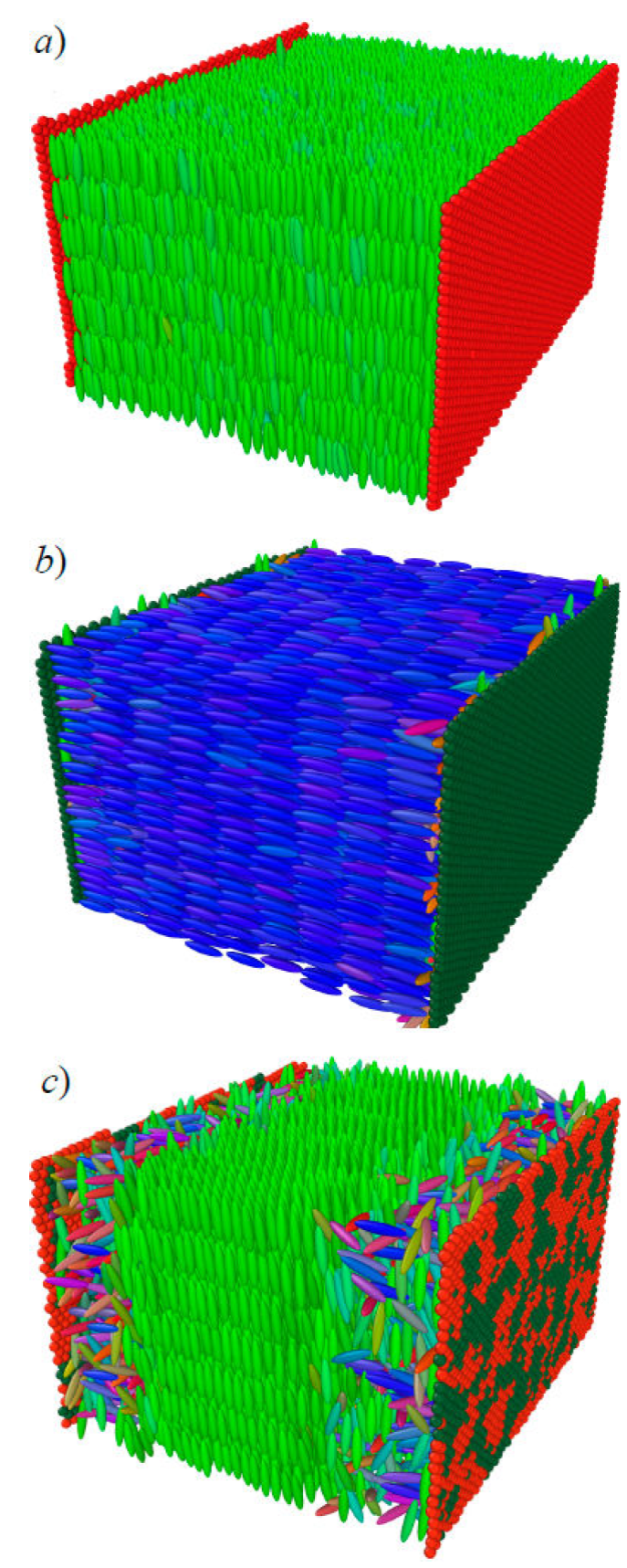
Figure 12 A calamitic sample confined between two substrates. The substrate wall exerts planar anchoring in a) and homeotropic anchoring in b). A concentration-dependent case c) leads to concentration fluctuations of wall particles and competing anchoring modes. Domains of wall particles in c) probe the local arrangement of the confined LC sample.
Our enhanced model for confined substrates makes it possible to explore how phase transitions shift when compared to the bulk, based on the type of anchoring used. This issue is of interest in thermotropic LC systems limited by extreme operating conditions. Equally important is a systematic study on how spatial ordering, with a detailed microscopic description of the boundary, is conveyed from the boundary to the bulk. An ongoing study in our group is centered on identifying optimal length scales for the transmission of orientational order from the boundary to the bulk region of the slab.
3.9. Liquid crystal droplets
Another paradigm for confinement consists of LC droplets. Here, the mesogenic fluid is contained in a spherical cavity defined by LJ particles. Confinement imposes spatial and orientational constraints on the LC sample. Boundaries used to confine samples not only induce surface effects, but they can also be recruited to transmit information into the bulk, far from the confining wall [135]. The rich response of the underlying mesophases is evident through changes involving temperature (thermotropic LCs), density (lyotropic LCs), external fields [136] (electric, magnetic, or hydrodynamic flux), and spatial constraints [137]. Confined LC samples experience a disruption of the underlying mesophase symmetry compared to the bulk. Examples of these systems include cells [86,138], spherical droplets [67], and cylindrical pores [67,139]. Studying the response of the nematic field to confinement, for example, is essential for developing a host of applications, such as those connected to screen [140] and sensor [141] technologies.
The interplay between long-range elastic energy and surface energy is an important contribution to consider in confined systems. Previous experimental, theoretical, and computational studies on confined systems include planar geometries [142-144] with blue phases [145], colloidal inclusions [10,23], spherical droplets [146,147], and cylindrical cavities [148,149]. Some LC configurations, such as the radially twisted-axial and axially-twisted planar bipolar have been reported [149]. These theoretical studies shed light on the conditions favoring specific phases in terms of spatial metrics and energy parameters (i.e., Frank elastic constants) [150,151]. On another front, Xu and Crooker [152] have focused on chiral nematic microdroplets with parallel surface anchoring using polarized microscopy: they report a phase stability diagram in radii and intrinsic pitch space, where twisted bipolar and Frank-Pryce structure regions emerge. Vanzo and coworkers [153] used MD simulations to study freely suspended GB nanodroplets, which exhibit chiral ordering and form ellipsoidal droplets. These authors also found that varying the size of the nanodroplets results in spontaneous symmetry-breaking of the surface bipolar director, yielding a twisted pattern.
Our LC nanodroplet system consists of a spherical droplet boundary formed from LJ particles taking the place of surfactant or solvent particles and an LC interior of calamitic mesogens, as shown in Fig. 13. The particles making up the droplet boundary are restricted to move only on the surface of the droplet of fixed radius R [154]. Mesogens interact via a modified GB potential [53,68,155,156]. This mixture gives rise to three types of interactions: LJ-LJ (surface-surface), GB-GB (bulk-bulk), and GB-LJ (bulk-surface anchoring) types. Shown in Fig. 14 are sample configurations when the droplet surface is purely water-based or surfactant-based from our previously published work [67]. Spatial constraints imposed by the geometry of the droplet prompt the formation of topological defects within the LC core driven by the anchoring mode: a bipolar defect is observed with planar anchoring (surfactant boundary), whereas a radial defect is evident with homeotropic anchoring (solvent boundary). Patterned surfaces are also possible by using water-surfactant mixtures for the droplet boundary, the results of which are reported elsewhere [67].
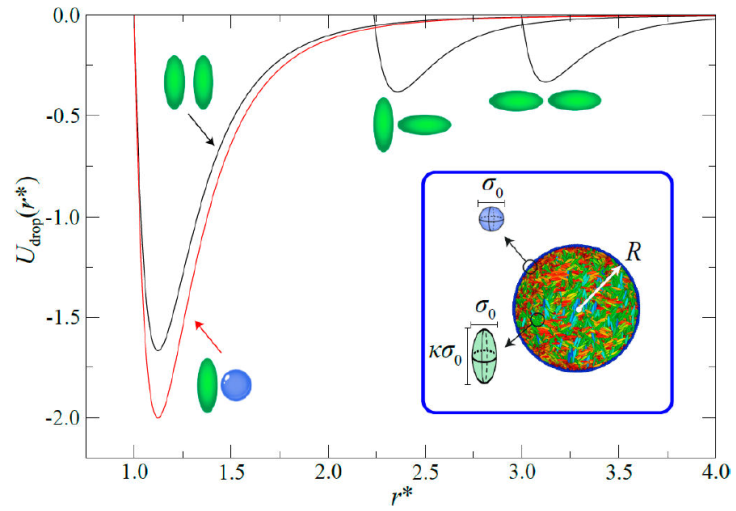
Figure 13 Contributions to the interaction potential for droplets, denoted U drop (r * ). Implicit are interactions between mesogens, droplet-boundary particles, and cross interactions. Shown are U GB (r * ) (black curves) and U cm (r * ) (red curve) with molecular schematics as a guide. Intermolecular length scales are normalized by σ 0. The inset shows the droplet model: calamitic mesogens have a width σ 0 and a length 𝜅σ 0. The droplet boundary consists of LJ particles of diameter σ 0. The droplets have a radius R.
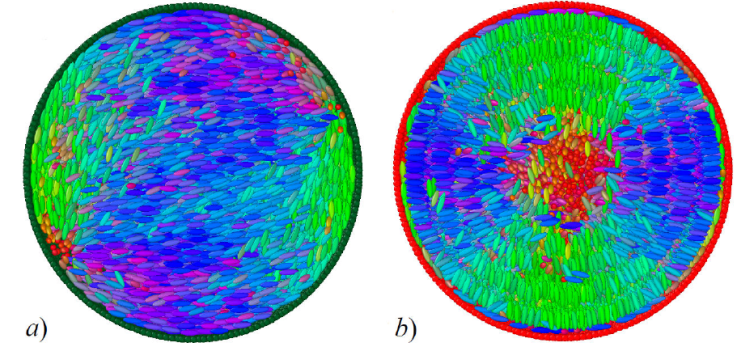
Figure 14 Snapshot cross-sections of LC droplets. Mesogen colors denote molecular orientation. Droplet surface color denotes composition: water (green spheres) or surfactant (red spheres). a) A bipolar defect emerges in the absence of surfactant. b) A radial defect appears when the droplet surface consists of surfactant only. Cases for different surfactant concentrations are reported in a previous study [66].
An application of these mixtures is the preparation of patterned surfaces by varying the ratio between solvent and surfactant comprising the nanodroplet wall. This approach has been studied by probing “interfacial templates” on a nanodroplet surface emerging from the underlying anisotropic fluid [67]. These templates can produce superstructures by adding multiple “building blocks” together [157]: once a set of nanodroplets have latched via nanodroplet interfacial events, this “block” can then add to another “block”, and so forth. Geometrical requirements can be programmed by functionalizing surfactant molecules comprising the nanodroplet interface. Fine-tuning structures attained by chemical functionalization is another tool available for synthesizing self-assembled structures via hierarchical self-assembly.
3.10. Dimensionality and confined liquid crystal samples
A host of applications in our everyday experience, including displays, biosensors, and electro-optical devices function via LC mesophases. Although much research has focused on mesophase appearance, stability, and behavior in three-dimensional (3D) samples, there is renewed interest in two-dimensional (2D) analogs. Not only are 2D platforms of interest in LC-sensitive films, but confinement (even quasi-confinement) in 2D induces phase changes due to large fluctuations in systems of reduced dimension [66,158,159]. These 2D systems allow access to features not easily extrapolated to or nonexistent in their 3D counterparts.
Applications of 2D systems are also relevant from a materials design perspective. For example, mixtures of mesophases with nanocrystals in 2D layers have been used to create structures [160-162]. For these and other applications, the mesophases present and the entropic forces acting on the anisotropic particles are issues to consider in their development [163-166]. Dynamical features are also often more pronounced, leading in some cases to the implementation of both switching technology and hierarchical (slab-based) synthesis of superstructures [66].
Recently, we reported our findings on the formation of topological defects in a 2D mesogenic system confined in different geometries [66]. Here, we focus on a circular boundary consisting of LJ particles. In our study, homeotropic or planar anchoring is possible by tuning the mesogen-wall interaction. We traced defect stability as a function of temperature using MD simulations. Analysis of system trajectories establishes that topological defects undergo fluctuations in position and intensity, diminishing at low temperatures as expected.
The behavior for planar and homeotropic anchoring of the circularly-confined LC system is summarized in Fig. 15. The ratio between the radial dimension of the boundary and the mesogens comprising the sample affect the structures observed [167,168]. In our case, the radial dimension of the boundary leads to a two-defect structure in either case but is distinct when considering the anchoring mode. For planar anchoring, defects are localized on opposite ends of the confining wall: the resulting state is a layered mesophase similar to a smectic arrangement save the thin surface shells on opposite ends, as seen in Fig. 15a). Under homeotropic anchoring, the defects remain separated from one another but localized away from the confining wall: the orientation induced by anchoring is overcome by internal thermal fluctuations of the system, as shown in Fig. 15b).
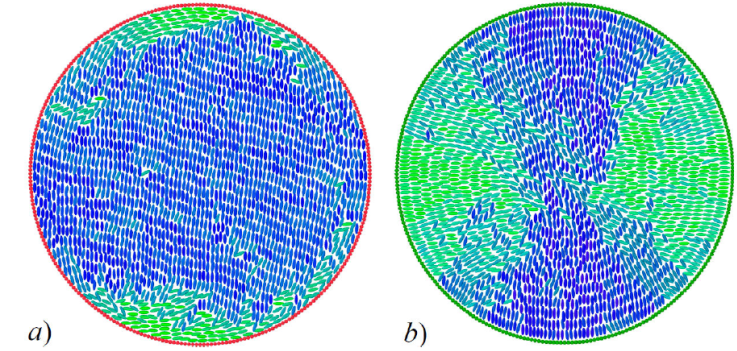
Figure 15 Snapshots for a 2D LC sample confined in circular geometry. Mesogen colors denote orientation. Boundary color denotes anchoring: a) planar, and b) homeotropic. A detailed comparison of spatial arrangements and underlying dynamics of these systems are reported in a previous study [65].
Molecular self-assembly and organization in 2D systems pave the way to prepare planar scaffolds to fix colloidal particles according to the arrangement of defects in the confined mesogenic sample [169-176]. The paradigm envisaged consists of preparing slabs of geometrically ordered colloidal substructures. In a subsequent step, 3D metamaterials form by stacking the slabs. Practicable layer-by-layer protocols [177-192] have the potential to broaden the gamut of materials attained by conventional 3D-based methods. Surfactant dispersions used to confine LC samples can be used to encode spatial information leading to specific arrangements [66,67]. Structured colloidal assemblies via topological defects can impart screw/twist symmetry in colloidal assemblies [193-196], thereby facilitating the production of chiral materials. Switching dynamics controllable through external fields (i.e., electric, magnetic, photonic, etc.) can be integrated into these materials as an additional feature [197-206]. Such an enhancement would be of particular interest in the design of LC-based devices [199,203,207-210].
4. Conclusions
This brief review focused on heterogeneous mesogenic systems. We considered mixtures under these scenarios: (1) binary mixtures consisting of mesogens with different aspect ratios, (2) colloidal inclusions immersed in a mesogenic solvent, and (3) LC samples confined by a boundary of Lennard-Jones particles. The Gay-Berne representation is used as a coarse-grained representation of mesogenic molecules in all cases.
One system of interest, particularly tied to the fabrication of metamaterials, is that of nematic colloids. Samples consist of colloidal inclusions immersed in a mesogenic solvent. Such inclusions disturb the orientational order of the nematic mesophase resulting in the formation of topological defects. On a physical basis, this effect materializes due to molecular anisotropy: we focused here on calamitic and discotic cases. The sensitive response of LC samples to topological defects has been exploited in many sensor-based technologies. The type of defects observed depends on the anchoring mode of a colloidal surface. Homeotropic anchoring leads to the formation of a Saturn ring around the colloidal inclusion. Planar anchoring yields boojums. The computational model used in this work involves extending the classical Lennard-Jones interaction to account for a mixture of spherical (colloids) and anisotropic (mesogenic) particles.
Topological defects arising from inclusions in a mesogenic solvent can couple with one another, providing an interesting platform to induce the self-organization of colloidal units into specific patterns. In our studies, we considered the simplest of cases: a nonbonded dyad of colloids. The orientation between the intercolloid vector and the mesophase director governs the coupling mode between topological defects. In this study, we highlighted the case for homeotropic anchoring in a discotic solvent. When the director and intercolloid vector are in a perpendicular arrangement, the system yields a triad of coupled Saturn rings: two parallel rings in which their planes contain the intercolloid vector and a third “bridging” ring perpendicular to the other two rings, appearing in the middle of the two colloidal inclusions. This arrangement has the ability to produce strongly-coupled colloidal assemblies.
The dynamical response of topological defects under flow was studied by leveraging the time evolution of ensemble trajectories from MD simulations. The Ericksen number E r serves as a metric that takes into account solvent flow rate. When E r is low, a topological defect remains unaffected. As E r increases and reaches a threshold value, the topological defect is displaced from the colloidal particle. At even higher values of E r, the defect detaches from the colloidal particle and eventually vanishes.
Finally, we considered confined systems in two cases: nanodroples and 2D cells. One important application connected to spatially restricted samples is extending the range of state points in which oriented mesophases are stable. An additional point is that most LC-based devices make use of a miniaturized implementation where finite-size effects are relevant. For our study, we confined mesogenic samples using Lennard-Jones particles. The type of anchoring at the boundary dictates the internal configuration of the mesogenic sample, resulting in characteristic defects. Planar anchoring leads to a bipolar defect in droplets similar to the arrangement observed in 2D samples. Homeotropic anchoring produces a radial defect in droplets and an analogous form is observed in the 2D system.
For each mixture explored in this review, we offered concluding remarks highlighting how it contributes to molecular organization, system dynamics, or self-assembly. Our primary goal was to highlight the rich mesophase behavior attainable with LC mixtures. For instance, specific topological defects can be tuned according to mesogen type, colloidal anchoring, or mode of confinement. In this way, desirable material properties can be scoped through computer simulations or via experiments after mapping a coarse-grained representation to a realizable chemical system. Many examples can be found in the literature in which theoretical and computational models have experimental counterparts [8,10,24,25,33,80,176,211-231]. Although protocols for self-assembly or molecular organization are beyond the scope of this review, we centered our discussion on mesophase behavior to pique the reader’s interest in LC-based metamaterials. The tools we developed for the systems highlighted in this review allow us to model and characterize LC systems of increasing complexity. The systems referenced here comprise a token of the range of possibilities for future work on LC materials.











 nueva página del texto (beta)
nueva página del texto (beta)



