1. Introduction
In order to search for renewable energy, researchers have recently been interested in thermoelectric materials that convert heat into electricity. Therefore, it is necessary to improve the conversion efficiency between thermal and electrical energy as much as possible. The efficiency of these materials is generally overseen by its figure of merit (ZT) specified as ZT = (S 2 .σ.T/k). In this equation, S, σ, T, and k are the mean Seebeck coefficient, the electrical conductivity, the absolute temperature, and the thermal conductivity, respectively [1].
The discovery of Heusler alloys has attracted the interest of many researchers due to their interesting properties in practical applications such as magneto-electronic and spintronics [2,3]. In addition to spintronic devices, Heusler alloys present several types of applications, particularly in the fields of thermodynamics [4], thermoelectric [5] and optoelectronics [6].
Very recently, a number of works have studied the thermoelectric response of a semiconducting quaternary Heusler alloy [7-9]. These works demonstrated that this type of compounds can be used as a thermoelectric material due to their high thermoelectric properties (e.g., Seebeck coefficient, thermal conductivity, electrical conductivity, power factor, and figure of merit).
Heusler compounds without transition metal elements, sp or d0 compounds have recently been subject of interest, because of their potential use in the production of thermoelectricity, spintronics, opto-electronics, etc. [10-16]. Due to the semiconducting behavior and tunable band gap properties, this type of Heusler compounds have received much attention. To our knowledge, up to now, no study on semiconducting and thermoelectric properties for our d0 quaternary Heusler compounds CaKNaZ (Z = Si, Ge, Sn) has been reported in the literature.
In this draft, the structural, mechanical, electronic and thermoelectric properties of new quaternary d0 Heusler compounds CaKNaZ (Z = Si, Ge, Sn) have been studied using the full potential linearized augmented plane wave method. The characteristics of energy bands and also the thermoelectric properties of CaKNaZ (Z = Si, Ge, Sn) compounds such as Seebeck coefficient, electrical and thermal conductivity in the large temperature range are discussed. This paper is systematized as follows. In Sec. 2, we define the theoretical back-ground. Results and discussion are contained in Sec. 3 and Sec. 4 is dedicated for the conclusions.
2. Computational method
In this study, various ground state results of CaKNaZ (Z = Si, Ge, Sn) were examined by a calculation procedure based on the density functional theory (DFT) [17]. The ground state structures, elastic and electronic properties were determined with full-potential linearized augmented plane wave method (FP-LAPW) implemented in the WIEN2k package [18]. The exchange-correlation potential was treated under the generalized gradient approximation (GGA) [19] and modified Becke-Johnson (mBJ) [20]. To achieve total energy convergence, the product of radius of muffin-tin spheres (Rmt) and cut-off for basis size (Kmax) that is, Rmt.Kmax = 8. The muffin-tin spheres radii for all atoms is taken to be 2.5 atomic units (a.u). To obtain well converged results, we used 8000 k-point, equivalent to a 20×20×20 k-point mesh, as base for the integration in the first Brillouin zone. The energy and charge convergence criteria during self-consistent cycles was selected as 10 -5 . The elastic constants were determined via IRelast package [21] implemented in the WIEN2K code. The thermoelectric properties were derived based on the semi classical Boltzmann transport theory using the BoltzTrap code [22] embedded in Wien2K code with a dense k-mesh of 50×50×50 to obtain accurate results. The electrons of Ca: 4s 2, K: 4s 1, Na: 3s 1, Si: 3s 2 3p 2, Ge: 4s 2 4p 2 and Sn: 5s 2 5p 2 are treated as valence electrons.
3. Results and discussion
3.1. Structural properties and formation energies
Our calculations begin by optimizing the cell volume in various atomic configurations. Generally, the quaternary Heusler compounds -LiMgPdSb- are represented by chemical formula X, X’, Y, and Z. From the structural point of view, these compounds are denoted as Y-type structures with F-43 m (space group 216) [23]. Depending upon the arrangement of atoms, one can arrange X, X’, Y, and Z atoms in three non-equivalent atomic configurations Y1, Y2, and Y3 as shown in Fig. 1, the Wyckoff positions [24]:
Type Y1: Ca(3/4, 3/4, 3/4), K(1/2, 1/2, 1/2), Na (1/4, 1/4, 1/4), Z(0, 0, 0).
Type Y2: Ca(3/4, 3/4, 3/4), K(0, 0, 0), Na(1/2, 1/2, 1/2), Z(1/4, 1/4, 1/4).
Type Y3: Ca(0, 0, 0), K(1/2, 1/2, 1/2), Na(1/4, 1/4, 1/4), Z(3/4, 3/4, 3/4).
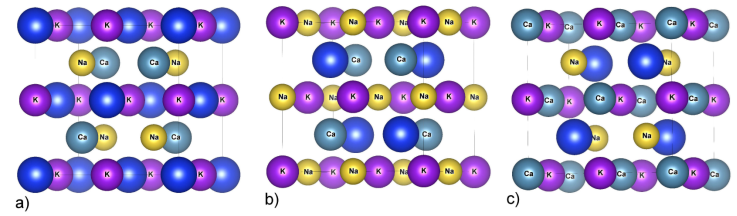
Figure 1 Atomic structures of a) type-Y1, b) type-Y2, and c) type-Y3 for the CaKNaZ (Z = Si, Ge, Sn) compounds.
We have checked the most stable structure by performing volume optimization in ferromagnetic (FM) and non-magnetic (NM) configurations states and the obtained curves are shown in Fig. 2. The results show that the NM-Y1 state is the ground state structure. However, the difference of energy between NM and FM state is found to be negligible. The calculations in the ferromagnetic phase show that the total magnetic moment is zero, which indicates the NM nature of the alloys. Thus, we conclude that both CaKNaZ (Z = Si, Ge, Sn) are NM in the stable Y1-type structure. After fitting the data by the Murnaghan equation [25], we determined the different values of the structural parameters at equilibrium for the three possible configurations of type: Y- (1), Y- (2) and Y- (3). All the results obtained are listed in Table I for all of the Heusler quaternary compounds CaKNaZ (Z = Si, Ge, Sn). As we have mentioned before, there are no experimental or theoretical data in the literature to compare with calculated structural parameters.
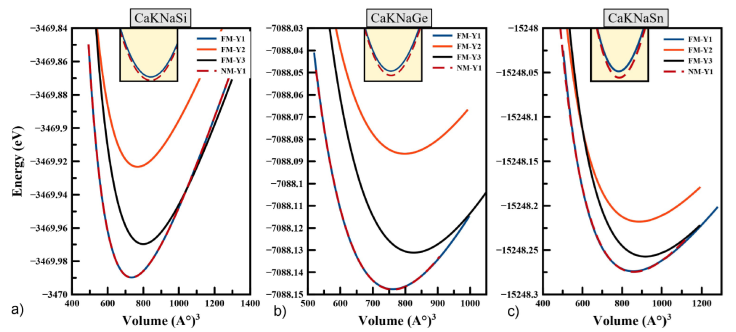
Figure 2 Total energy as a function of volume per formula unit (f.u.) in the type FM-Y1, FM-Y2, FM-Y3 and NM-Y1, NM-Y2, NM-Y3 for the CaKNaZ (Z = Si, Ge, Sn) compounds.
Table I Calculated total energies E tot (Ry) per formula unit, equilibrium lattice constant a 0 (Å), the bulk modulus B (GPa), the formation energy E form (eV) and band gap E g (eV) within GGA and GGA-mBJ for CaKNaZ (Z=Si, Ge, Sn) compounds in their different structures type and magnetic configurations.
| Alloy | Type | E tot | Favored | a0 | B | E form | E g | ||
|---|---|---|---|---|---|---|---|---|---|
| FM | NM | NM | NM | NM | GGA | mBJ | |||
| CaKNaSi | Y-1 | -3469.989778 | -3469.989805 | Y1(NM) | 7.58 | 22.4180 | -0.11 | 0.84 | 1.34 |
| Y-2 | -3469.923249 | -3469.924781 | 7.72 | 20.1310 | |||||
| Y-3 | -3469.969695 | -3469.972089 | 7.83 | 22.2739 | |||||
| CaKNaGe | Y-1 | -7088.147619 | -7088.147787 | Y1(NM) | 7.67 | 20.9814 | -0.73 | 0.44 | 1.33 |
| Y-2 | -7088.086561 | -7088.086849 | 7.80 | 17.9675 | |||||
| Y-3 | -7088.131147 | -7088.131958 | 7.88 | 20.6751 | |||||
| CaKNaSn | Y-1 | -15248.273885 | -15248.274613 | Y1(NM) | 7.98 | 20.2312 | -1.54 | 0.68 | 1.15 |
| Y-2 | -15248.217963 | -15248.218470 | 8.06 | 18.6790 | |||||
| Y-3s | -15248.257250 | -15248.257709 | 8.14 | 21.5119 | |||||
To ensure the thermodynamic stability of our compounds, we calculated the formation energy using [26]:
where E Ca, E K, E Na, E Z(Z= Si, Ge, Sn) represent the total energy per atom for Ca, K, Na, and Z (Z = Si, Ge, Sn) in the stable crystal, respectively. And E(CaKNaZ) represents the total energy of CaKNaSi, CaKNaGe and CaKNaSn alloys in the ground state. If the formation energy is negative, then the material can be said to be thermodynamically stable and can be considered in synthesis. As shown in Table I, we note that the formation energy of all compounds is negative. Which means all the alloys CaKNaZ (Z = Si, Ge, Sn) are thermodynamically stable and thus can be experimentally synthesized.
One of the fundamental criteria for stability is the cohesive energy, where defined as the energy necessary to separate a compound into its components. The expression of cohesive energy is written as [27]:
where
3.2. Mechanical stability and elastic properties
The mechanical properties of solids play a very important role in the choice of materials for a specific application. We calculated the elastic properties for a cubic structure to examine the mechanical stability of the compounds studied. The mechanical stability for a cubic material is determined by the following criteria:
C11 > 0; C11 > C22;
C11 - C12 > 0; C11 + 2C12 > 0 and C44 > 0.
In this work, using the generalized gradient approximation (GGA) we have calculated the elastic constants for CaK-NaZ (Z = Si, Ge, Sn) compounds, and are listed in Table II. It can be seen that the previous criteria are strictly followed by the observed lattice constants and thus their mechanical stability was confirmed.
Table II Calculated elastic constants Cij (GPa), Bulk modulus B (GPa), Voigt shear modulus Sv (GPa), Poisson ration V, Young modulus Y(GPa), (B/Sv) ratio and anisotropic factor A.
| Alloy | C 11 | C 12 | C 44 | B | S v | B/S v | Y | V | A |
|---|---|---|---|---|---|---|---|---|---|
| CaKNaSi | 43.7240 | 13.3681 | 25.3655 | 23.486 | 21.290 | 1.10 | 49.049 | 0.151 | 1.69 |
| CaKNaGe | 39.4850 | 11.3631 | 23.2304 | 20.737 | 19.562 | 1.06 | 44.646 | 0.141 | 1.65 |
| CaKNaSn | 35.1386 | 12.0832 | 21.7112 | 19.768 | 17.637 | 1.12 | 40.782 | 0.156 | 1.88 |
In addition, based on elastic constants, we further calculate various other parameters of mechanical property such as the Voigt bulk modulus (B), Voigt shear modulus (SV), Voigt Young’s modulus (Y), anisotropic factor (A), and Voigt Poisson’s ratio (V), which are presented in Table II. The brittle/ductile nature of a material can be guessed from the value of B/SV ratio. If B/SV ratio is superior to 1.75, then the material is said to be ductile in nature, if not, it is brittle [28]. Here, we noticed that B/SV ratio is less than 1.75 for the three compounds CaKNaZ (Z = Si, Ge, Sn), thereby, confirming that the three compounds have brittle nature. These results can also be further confirmed by calculating the Voigt Poisson ratio (V). Overall, brittle materials have V < 0.33 and ductile ones have V > 0.33[29]. The results shown in Table II explains that the three compounds are brittle. Also, for perfect isotropic material the anisotropic factor A should be equal to one, otherwise, the material is anisotropic. The calculated elastic anisotropic factor for CaKNaZ (Z = Si, Ge, Sn) compounds is different than 1, indicates these compounds are not elastically isotropic.
3.3. Electronic properties
In order to precisely understand and study the electronic state, the band structures of CaKNaZ (Z = Si, Ge, Sn) compounds were calculated using GGA-PBE and GGA-mBJ approximations, have been plotted in Fig. 3. In all cases, CaKNaZ (Z = Si, Ge, Sn) compounds are semiconductors. The GGA approximation typically underestimates the energy gap, while the mBJ approximation which is the most suitable for the calculation of the band gap because it gives results close to the experiment [30]. The GGA-PBE calculations display that CaKNaSi and CaKNaSn have an indirect band gap (the top of the valence band for CaKNaSi and CaKNaSn compounds lies at the Γ-point, while the bottom of the conduction band lies at the X-point) and CaKNaGe has a direct bandgap (the top of the valence band and the bottom of the conduction band for CaKNaGe lies at the Γ-point). While The GGA-mBJ calculations show that all our compounds have an indirect band gap with values of 1.34, 1.33, and 1.15 for CaKNaSi, CaK-NaGe and CaKNaSn respectively. The results are listed in Table I.
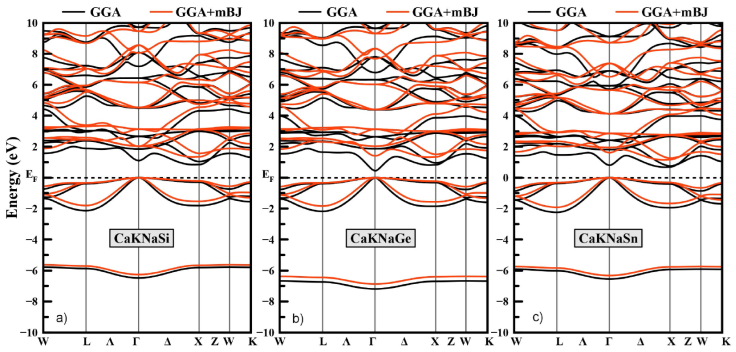
Figure 3 Electronic band structure for the CaKNaZ (Z = Si, Ge, Sn) compounds at their equilibrium lattice constant obtained by GGA-PBE and GGA-mBJ.
To better understand the electronic structure, we plotted the total and partial density of states (DOS) for the CaKNaZ (Z = Si, Ge, Sn) compounds in Fig. 4. As can be seen, the global appearance of TDOS and PDOS is similar for all three compounds and, consequently, can be grouped together. In all compounds, the valence band in the lower energy partition from -6.36 eV to -5.46 eV in CaKNaSi, from -6,8 eV to -6.3 eV in CaKNaGe and from -6.3 eV to -5.6 eV in CaKNaSn are dominated by the Si-s, Ge-s and Sn-s respectively. Additionally, the maximum of valence band from -1.9 eV is principally represented by the hybridization between Si-p and Ca-p states, Ge-p and Ca-p states, Sn-p and Ca-p states. while, the contribution of K states is nearly zero. In addition, the minimum conduction band is dominated mainly by the Ca state. In all cases, the DOS at the Fermi level is zero, which demonstrates the semiconducting nature of these compounds and confirms the results of the band structure.
3.4. Thermoelectric properties
Thermoelectric materials have the property of converting thermal energy into electrical energy or vice versa. Today, Heusler compounds have been highly regarded by industry and scientific research for their thermoelectric behavior. Thermoelectric materials are characterized by three parameters: the Seebeck coefficient (S), the electrical conductivity σ=τ, and the thermal conductivity k/τ. In this study and for the first time, the thermoelectric properties of CaKNaZ (Z= Si, Ge, Sn) compounds are calculated by the BoltzTrap code with a dense k-mesh of 50×50×50 mentioned earlier. The thermoelectric properties of the quaternary heusler semiconductors CaKNaZ (Z = Si, Ge, Sn) have been calculated in Fig. 5a) to 5 c). In Fig. 5a) we have reported variation of the Seebeck coefficient (S) as a function of temperatures. We notice that S for CaKNaSi (CaKNaGe) is increasing from 245.29 V/K at 100 K (246.66 μV/K at 200 K) and attains a maximum value of 257.04 μV/K at 500 K (257.19 μV/K at 600 K). Then it decreases again. As for CaKNaSn, it decreases from 255.94 μV/K at 100 K and attains a minimum value of 248.57 μV/K at 300 K, then increases until it reaches a maximum value 256.83 μV/K at 800 K (259.32 μV/K at 800 K) and decreases again. The positive value of S indicates the p-type character of the alloys.
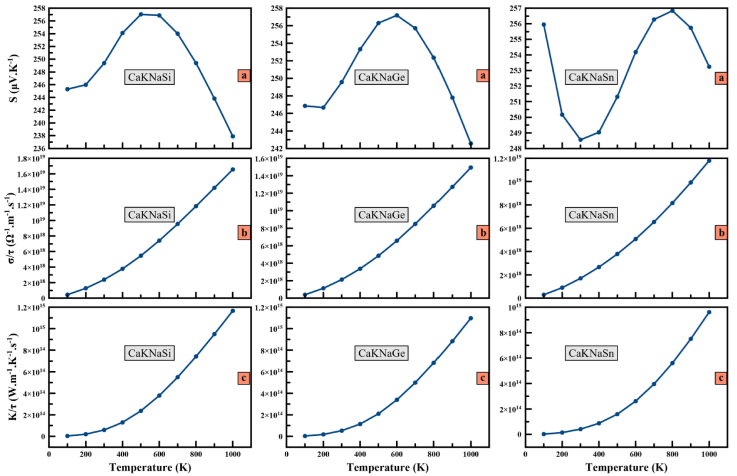
Figure 5 The variation of Seebeck coefficient S a), electrical conductivity σ/τ b) and thermal conductivity κ/τ c) versus temperature for CaKNaZ (Z = Si, Ge, Sn).
The electrical conductivity of CaKNaZ (Z = Si, Ge, Sn) compounds as a function of temperature is shown in Fig. 5b). We observe that σ/τ increases with rising temperature and attains a maximum value of 1.65 × 1019 and 1.49 × 1019 and 1.18 × 1019 Ω -1 .m -1 .s -1 for CaKNaSi, CaKNaGe, and CaKNaSn respectively. At 300 K, the electrical conductivity is 2.39 × 1018 Ω -1 .m -1 .s -1 , 2.13 × 1018 Ω -1 .m -1 .s -1 , and 1.70 × 1018 Ω -1 .m -1 .s -1 for CaKNaSi, CaKNaGe, and CaKNaSn, respectively.
In solids, electrons and phonons are responsible for heat transfer. In the present work, we present the results only for electronic thermal conductivity (k e /τ) of CaKNaZ(Z = Si, Ge, Sn) quaternary Heusler alloys. In the Fig. 5c), it can be seen that for CaKNaSi, CaKNaGe and CaKNaSn, the electronic thermal conductivity increases with temperature. The electronic thermal conductivity (k e /τ) calculated at room temperature has a values of 5.94 × 1013 W.K -1 .m -1 .s -1 for CaKNaSi, 5.29 × 1013 W.K -1 .m -1 .s -1 for CaKNaGe and 4.15 × 1013 W.K -1 .m -1 .s -1 for CaKNaSn.
The figure of merit ZT is a quantity determined to measure the overall thermoelectric performance of materials and compounds. The larger the ZT and therefore our material is more efficient from a thermoelectric point of view. The calculated the figure of merit for CaKNaZ (Z = Si, Ge, Sn) compounds as a function of temperatures is shown in Fig. 6. We note that the ZT values are almost stable at all temperatures, ranging between 0.750 to 0.803 for CaKNaSi, between 0.753 to 0.80 for CaKNaGe, and between 0.752 to 0.787 for CaKNaSn. The thermoelectric figure of merit is 0.750, 0.753, 0.761 at 300 K for CaKNaSi, CaKNaGe, CaKNaSn, respectively. The results of the figure of merit obtained suggest the good thermoelectric performance of our quaternary Heusler compounds and could be promising materials for applications in thermoelectric generators. The value of electrical conductivity, thermal conductivity, Seebeck coefficient and figure of merit ZT at room temperature are summarized in Table III.
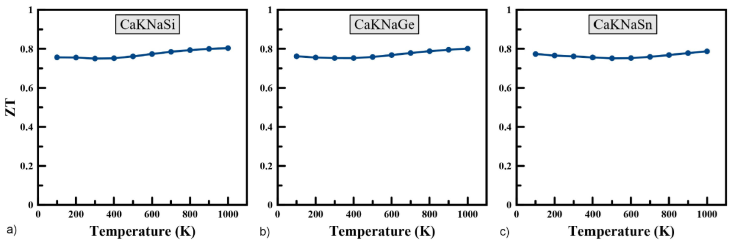
Figure 6 The variation of figure of merit ZT as a function of temperature for CaKNaZ (Z = Si, Ge, Sn).
Table III Values of electrical conductivity σ/τ (1018Ω -1.m -1.s -1), thermal conductivity κ/τ (1013 W.m -1.K -1.s -1) and Seebeck coefficient S ( μ V.K -1), and figure of merit ZT at 300 K for CaKNaZ (Z = Si, Ge, Sn) compounds.
| Compound | σ/τ | κ/τ | S | ZT |
|---|---|---|---|---|
| CaKNaSi | 2.39 | 5.94 | 249.37 | 0.750 |
| CaKNaGe | 2.13 | 5.29 | 249.56 | 0.753 |
| CaKNaSn | 1.70 | 4.15 | 248.56 | 0.761 |
4. Conclusion
Using an ab initio study based on the density functional theory and utilizing GGA-PBE and GGA-mBJ approximations, we have explored the structural, elastic, mechanical, electronic and thermoelectric properties of new quaternary Heusler CaKNaZ (Z = Si, Ge, Sn) compounds, for which we observed that the alloys are NM in the stable Y1-type structure. The obtained formation energy predicts that these alloys can be synthesized in experiments. Moreover, all compounds also fulfill the criteria of mechanical stability. The electronic properties computed indicate that the materials are semiconductors. In addition, the thermoelectric study of our compounds showed the Seebeck coefficient is found to have a positive value, thereby, declaring the p-type conductivity of the alloys. The values of ZT are noticed as 0.750, 0.753, 0.761 at 300 K for CaKNaSi, CaKNaGe, CaKNaSn, respectively. The overall properties observed confirm that the semi-conducting quaternary Heusler alloys, CaKNaZ (Z = Si, Ge, Sn), are promising candidates for thermoelectric applications at moderate temperatures. We expect our present theoretical estimation will pave a new direction to carry out the experimental research of the proposed alloys.











 nueva página del texto (beta)
nueva página del texto (beta)



