1. Introduction
The laser discovery, particularly the ruby pulsed one, allowed to P. A. Franken et al. in 1961 [1] the second harmonic generation (SHG) experimental observation, the authors reported the observation of the second harmonic at λ = 3472 Å, while a hight intensity monochromatic light of λ = 6943 Å hitting on a crystalline quartz sample. For the optical harmonic generation, even of higher orders, nonlinear dielectric coefficients are required, as it is clearly explained by Robert W. Boyd [2] in the traditional book of nonlinear optics. In fact, high intensity fields, as the ones involved in the intense laser physics field, can induce nonlinear dielectric coefficients. In fact, nonlinear optics is interesting and a widely studied topic, from its fundamental as well as from applied point of view. Although we are interested in the SHG, nonlinear optical properties are a rich field of possible effects. For instance, we can mention third order corrections to the absorption coefficient, relative changes in relative refractive index, nonlinear optical rectification, optical gain, third harmonic generations, among others.
In recent years, an important amount of nonlinear optical properties has been reported in the scientific literature, particularly those related with quantum confinement in which the potential profile asymmetry is present, because this is an important factor for the enhancement of nonlinear optical properties, because the dipole matrix element can be tuned and maximized. For instance, E. Rosencher and Ph. Bois [3], by means of compact density-matrix formalism, report important formulas for the second-order susceptibilities, specifically for the optical rectification and for the SHG and applied these to a step-like asymmetric Al x Ga 1-x As/GaAs quantum well (QW) and do the experiments as well, and report good agreement between theoretical model and experimental measurements, reporting an important optical rectification enhancement in comparison with GaAs bulk. P. Boucaud et al. [4] performed a detailed SHG analysis for an specific wavelength in Al x Ga 1-x As/GaAs asymmetric step-like QWs. E. Kasapoglu et al. [5] report the absorption coefficient as well as the refractive index change, considering third order nonlinear corrections, with expression obtained in the compact density-matrix, taking into account the effect of external applied electric field. We can give some other references discussing nonlinear optical properties enhancement [6-12].
Now, we would like to talk about the non-resonant intense laser field (ILF) effect, which is an important external factor that can modify the potential profile seen by the charge carriers, as reported by F.M.S. Lima et al. [13, 14]. In reference [14] the authors consider an ILF polarized perpendicularly to the heterostructure interfaces as well as at sufficiently high frequencies, in such a way that the potential is given by a laser-dressed one and concluded that a laser-dressing parameter α 0 > L/2, being L the single QW width, transition from single to double QW is predicted. E. Kasapoglu et al. [15] also report, that due to ILF effect, the transition from semi-parabolic QW to a kind of asymmetric double QW, affecting importantly the reported nonlinear optical properties, specifically the absorption coefficient and the relative refractive index change. Besides, C. A. Duque et al. [16] investigated the combined effects of ILF and externally applied electric field on GaAs exciton states as the ILF modify the potential profile from single to double QW. On the other hand, for the situation α 0 < L/2, the potential profile deformation, as reported by E. C. Niculescu et al. [17], is an analytical function of α 0, in fact an arccos(α 0) one, and they reported the binding energy as well as the density of states for an impurity in a rectangular QW, as a function of the laser-dresser parameter and on the donor impurity position. Also, in this same regime for the laser-dressing parameter (α 0 < L/2), E. Kasapoglu et al. [5] reported the effect of ILF, electric and magnetic fields on a step-like potential profile on the optical properties, reporting a red-shift in the absorption coefficient and in the relative refractive index change as the intense laser field effect increase. In general, the asymmetry is provided by different composition in each region of the heterostructure but it is also possible to induce this by external factors as electric and magnetic fields, and in this case also with the non-resonant ILF effect [18-21].
Finally, related with the SHG, as explained in the previous paragraphs, it is present in bulk materials as well as in systems with quantum confinement as reported in Refs. [1-3], as long as the second order susceptibly is different from zero or induced, for example by laser field effects. There exist several reports on this optical property in quantum confined systems. For instance, in 1995, A. Fiore et al. [22] carried out the experimental measurement of the SHG for symmetric AlGaAs/GaAs QW induced by an externally applied electric field (F) and report the SHG for a GaAs QW width of 50 Å between Al 0.4 Ga 0.6 As barriers with F = 50 kV/cm at λ = 1.66 μm. From the theoretical point of view, Imen Saidi [23] report the enhancement of SHG in asymmetric AlGaN/GaN/AlGaN heterostructure, and reported a significant intensity of the SHG signal. The SHG study as a function of external electromagnetic field for parabolic quantum dots is recently reported in [24]. The enhancement of the SHG for III-Nitride QW by means of metamaterials is studied by N. Nouri and M. Zavvari [25]. Some other recent reports on the SHG [26, 27], and references therein.
In this paper we systematically studied the combined effect of the ILF, in the α 0 < L/2 regime, here L represents the narrower potential profile region, being in this case the central barrier width L cb (see Fig. 1, where all the geometrical parameters are depicted), and an inplane (x-directed) magnetic field on double asymmetric Al x Ga 1-x As/GaAs QW with the aim to enhance the SHG response by identifying the the geometric parameters that generate the resonance condition and considering the effect of the external fields.
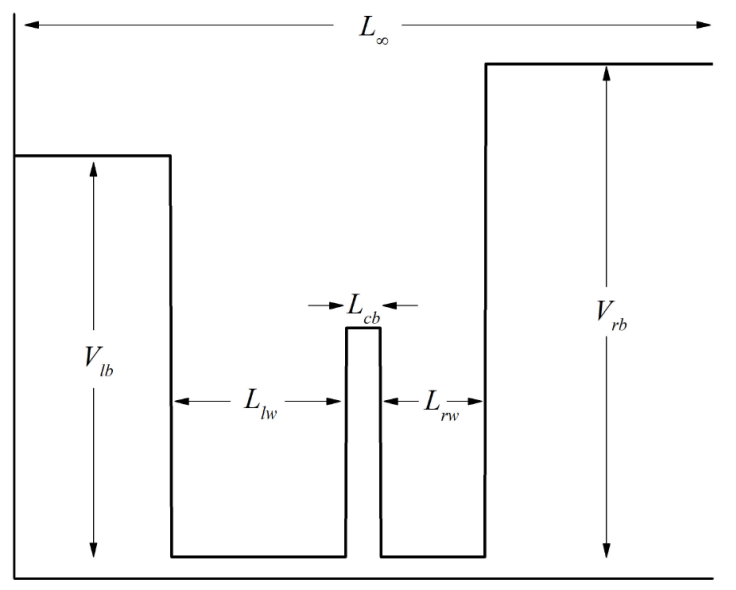
Figure 1 Potential profile schematic representation for the asymmetric double Al x Ga 1-x As/GaAs QW. Here we specified all the involved geometrical parameters used all along the manuscript, except for the central barrier potential height (V cb ).
The organization of the paper is the following: In Sec. 2 we introduce the implemented theoretical framework, then Sec. 3 shows the results and discussion, and finally the main conclusions are given in Sec. 4.
2. Theoretical Framework
In this paper we report the electronic structure as well as the SHG for asymmetric Al x Ga 1-x As/GaAs double quantum well (ADQW) considering a high frequency, non-resonant, ILF effect and an in-plane (x-directed) magnetic field. This was done within the effective mass approximation and the conduction band offsets are computed by using the solid model theory (SMT) [28, 29].
The time-independent Schrödinger equation of the system is given by:
Here ħ stands for the reduced Planck constant,
Table I Computed parameters in the model solid theory for the constituent materials using the Vegard’s law for Al x Ga 1-x As, except for the Eg where the bowing parameter is considered.
| Al 0.15 Ga 0.85 As | Al 0.25 Ga 0.75 As | Al 0.30 Ga 0.70 As | |
|---|---|---|---|
| ε r (e) | 12.474 | 12.190 | 12.048 |
| a (nm) | 0.565 | 0.565 | 0.565 |
| E g (eV) | 1.618 | 1.756 | 1.828 |
| Δ so (eV) | 0.332 | 0.326 | 0.323 |
| E v;av (eV) | -7.005 | -7.062 | -7.091 |
| V c (meV) | 105.17 | 184.54 | 227.00 |
As described in Table I caption, here we are taking into account the bowing parameter for the Al x Ga 1-x As energy band-gap, given as
Here b = -0.37 stands for the deviation of the well known Vegard’s law linear interpolation. The structural potential profile V c (z) is an ADQW, depicted in Fig. 2 with continuous black solid-lines, that will be affected by the considered external factors. In Fig. 2 we present the effect of the laser dressing-parameter a) and the magnetic field b) on the potential profile as well as on the probability amplitudes for the ground (black-lines), first excited (red-lines) and second excited (blue-lines) states, for the chosen values specified in the figure. When we consider the ILF effect in the high frequency limit the electron is subject to a time-averaged potential [13, 14]:
The laser-dressing parameter α 0 is defined as
where Ω and A 0 stands for the frequency and the amplitude of the potential vector of the laser field, respectively.
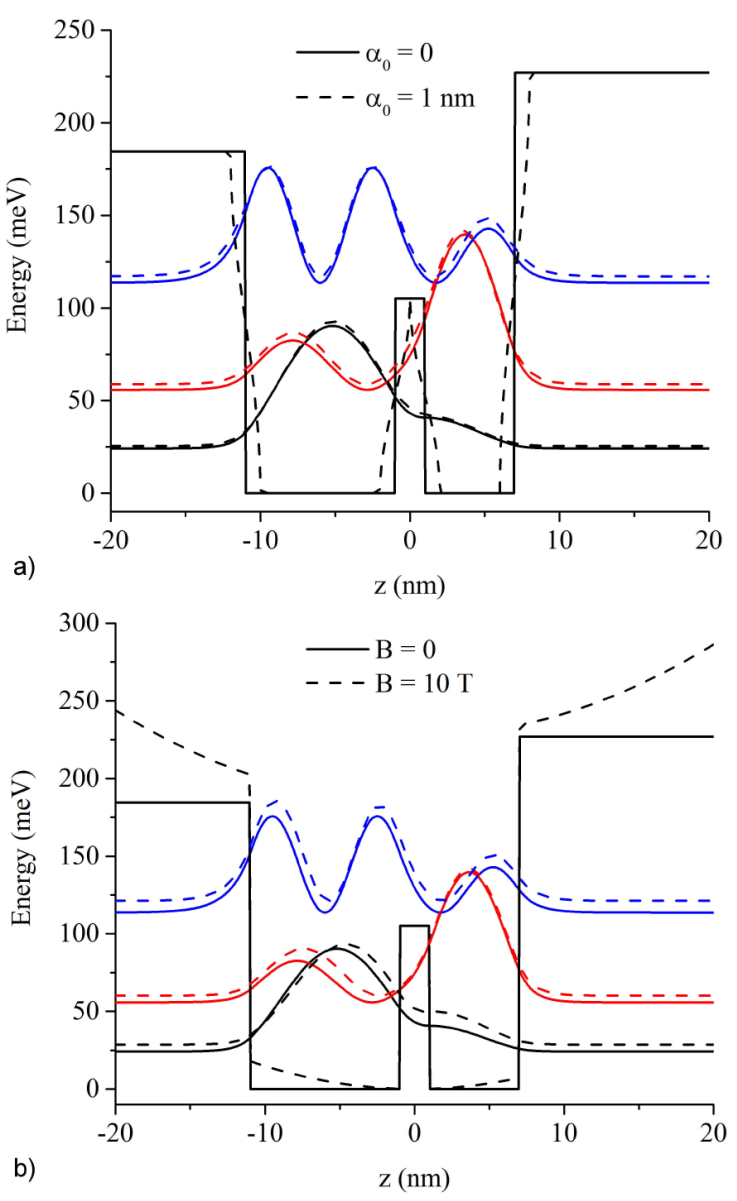
Figure 2 Potential profile and electronic structure for asymmetric double Al x Ga 1-x As/GaAs QW. In a) we depict the electronic structure for zero and α 0 = 1 nm ILF effect. In b) the B = 0, and B = 10 T electronic structure is presented. Ground, first and second excited states, are labeled with black-, red- and blue-lines, respectively.
The method that we use to solve the Eq. (1) is the well-known diagonalization procedure. So, by expanding the envelope function as follow,
we can compute the Hamiltonian matrix for the Hamiltonian in Eq. (1)H mn = 〈ψ mǀHǀψ n〉, that include the matrix elements for kinetic energy term, the quadratic potential profile due to the in-plane magnetic field as well as the laser dressing potential matrix elements that considers the double QW confinement potential, and after diagonalize this matrix we obtain the c m coefficients and the energies E n . Here L 1 stands for the infinite barrier rectangular QW width, of the complete orthonormal set for the envelope function expansion. Besides Eq. (5) has an infinite sum of terms, from the physical point of view is necessary just a matrix that ensures the energy convergency, that in this case is for n = 100.
Once computed the electronic structure for the system, the dipole matrix element is given by:
that allows to compute the coefficients corresponding to the susceptibility of second order that give the SHG, being ψ i (z) and ψ j (z) the initial and final states, following the lines of E. Rosencher and Ph. Bois [3]:
were ε 0 is the vacuum permittivity, ρ represent the system charge density, ω stands for the incident photon angular frequency and ħΓ j = ħ/T j are the damping terms associated with the mean lifetime due to intraband dispersion rate. Finally, the energy differences are given E ji = (E j - E i ). We must stress here that the SHG is generated by an extra laser, not the one that induces the laser-dressing potential, but a resonant one.
3. Results and discussion
Electronic properties as well as SHG results are presented and discussed in this section for Al x Ga 1-x As/GaAs ADQW. As mentioned in the previous section, we are working within the effective mass approximation and the band-offsets are determined by means of the model solid theory, with the parameters listed in Table I. The chosen aluminum concentration (x) for the left-, central- and right-hand barriers are: 0.25, 0.15 and 0.30, respectively. On the other hand, the right-hand well width is fixed to L rw = 6:0 nm with a central barrier of L cb = 2 nm. In the following, we will present the results as a function of L lw , ranging from 2 up to 16 nm, and as a function of the in-plane (x-directed) magnetic field of strength B, with and without intense laser field effect.
In Fig. 3a) is shown (E 1 - E 0) as well as the value of (E 2 - E 0)/2 for the system as a function of the left-hand side QW L lw , without any ILF (black solid lines) and with a laser-dressing parameter of α 0 = 1 nm (blue dashed lines). Figure 3b) shown the same energy differences, but in this case for B = 0 (black solid lines), B = 5 T (red dash-dot lines) and B = 10 T (blue dash-dot-dot lines). The aim of this study was to determine the intersection of both quantities that makes the SHG, given by Eq. (7), to be a sharp function. The first crossing in 3a) can be observed for L lw about 2.8 nm (at 72 meV) and 2.9 (at 71 meV) for α 0 = 0 and α 0 = 1 nm, respectively. Then, as L lw increases, we observe a second crossing at L lw about 13.8 nm (at 31 meV) and 13.7 (at 32 meV), for the same values of α 0, and we can clearly see that the ILF slightly modify the energy levels. Now, in Fig. 3b) we report these curves for B = 0, that has the same crossing as for α 0 = 0; Then, with red dash-dot lines, we present the results for B = 5 T and we observe that the first energy crossing is for an smaller L lw value and it experiences a blueshift, and the second energy crossing increase further in the L lw QW width but now with a redshift; Finally we report the case for B = 10 T, in the region of L lw ∈[2,16] and there is not any energy crossing, that will imply that the SHG resonant condition will not be fulfilled, at least not for chosen set of parameters.
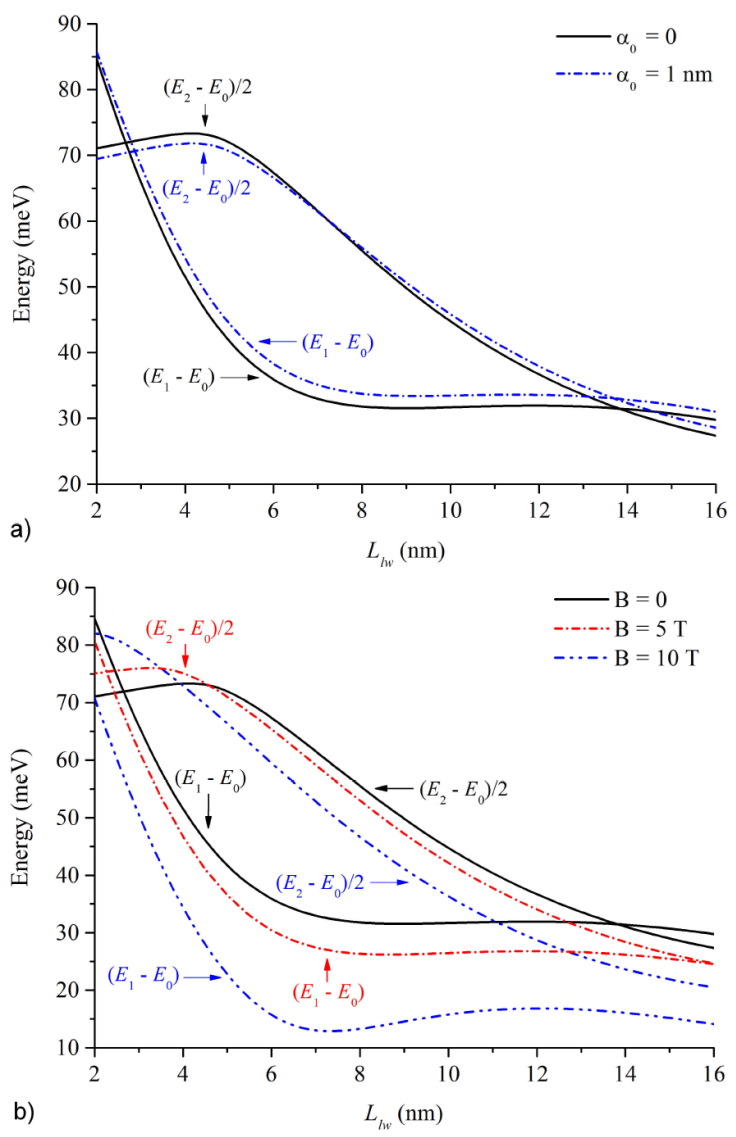
Figure 3 Main energy level difference (E 1 - E 0) as well as the value of (E 2 - E 0)/2 for the ADQW as a function of the left-hand side QW width L lw . In a) we present these for α 0 = 0 and α 0 =1 nm, while in b) these are shown for B = 0, B = 5 T and B=10T.
Dipole matrix elements (DME) ǀM ij ǀ and the product of them ǀM 10 M 12 M 20 ǀ, as a function of L lw , taking into account ILF effects (α 0) and external magnetic field (B) are shown in Fig. 4. In Fig. 4a), the DME for the main transition ǀM 10 ǀ is represented with black lines, the intermediate one ǀM 12 ǀ with red lines, while the second to ground state ǀM 20 ǀ is given with blue ones. In Fig. 4b) the product of then in shown (in all the cases the continuous line is for α 0 = 0 and dashed ones for α 0 = 1 nm). Observe that, in general, the ILF effect slightly modify the DME behavior and that the factor ǀM 10 M 12 M 21 ǀ start to increase for L lw > 6 nm, all this is for B = 0. On the other hand, with α 0 = 0, in Fig. 4c) we present ǀM ij ǀ for B = 0 (continuous line), 5 T (dashed line), and 10 T (point-dashed lines), with the same color-code as in Fig. 4a) for the involved DME, while in Fig. 4d) the product of them is shown. In this case we can see that the magnetic field has a more pronounced effect on individual DME that strongly affect the product of them ǀM 10 M 12 M 20 ǀ, and eventually will be reflected in the SHG signal. In general, the ǀM 20 ǀ vanishes for L lw about 5.5 nm because the the envelope functions of the ADQW are nearly symmetric, and this becomes important for L lw > 6 nm, except in the case of B = 10 T that becomes minimum for L lw around 12 nm, that is due to the strong fall in the 〡M 10 〡 value and, as we will analyze in the following, this has important implications in the SHG behavior.
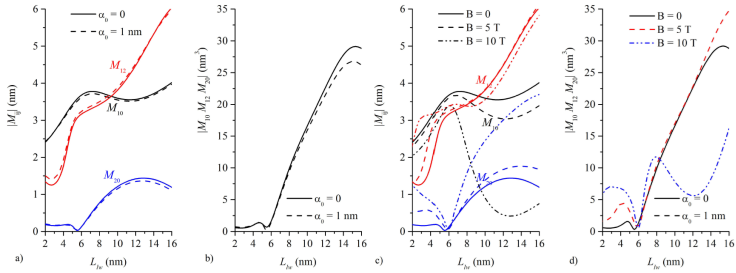
Figure 4 Dipole matrix elements ǀMijǀ in a) and c), and the product of them ǀM 10 M 12 M 20 ǀ in b) and d), as a function of the left-hand side QW width L lw . In the first line plot, this is shown for α 0 = 0 and for α 0 = 1 nm, while in the second one these are for B = 0, 5, and 10 T.
Figure 5 shows second harmonic generation for the system considering the ILF effect, as a function of the incident photon energy, for four values of L lw ; a) 10 nm, b) 12 nm, c) 14 nm, d) and 16 nm, that are within the region of higher values for the dipole matrix element product ǀM 10 M 12 M 20 ǀ and include the second energy level crossing, as a function of L lw , as shown in Figs. 3a) and 4b). The SHG is given by Eq. (7), as reported by E. Rosencher and Ph. Bois [3], that is formally defined when the energy difference of the first excited and ground state coincides with the energy difference from second excited state and the first excited one, in this case the energy crossing in Fig. 3. Out of this condition, this can be interpreted as a sum-frequency generation, as defined by Robert W. Boyd [2]. So, in Fig. 5a) we report the results for L lw = 10 nm and we observe two peaks because the energy level difference do not coincide and the ILF effect characterized with α 0 = 1 nm induces a blueshift in the curve. In Fig. 5b), for L lw = 12 nm, the two peaks become closer and the intensity increases almost four times with the shift toward higher energies due to ILF effects. In Fig. 5c) we show the results for L lw = 14 nm, that is very close to the energy difference crossing, where the SHG condition is fulfilled, and it is clear that the amplitude is much more important, and that the ILF effect keep the blueshift but the amplitude decreases. Finally, in Fig. 5d) we can see that an small shoulder about 30 meV in the incident photon energy, in both cases, and the magnitude start to decrease. Finally, it is clearly seen from those four figures that the SHG peak shifts towards lower energies with the increase of the QW width.
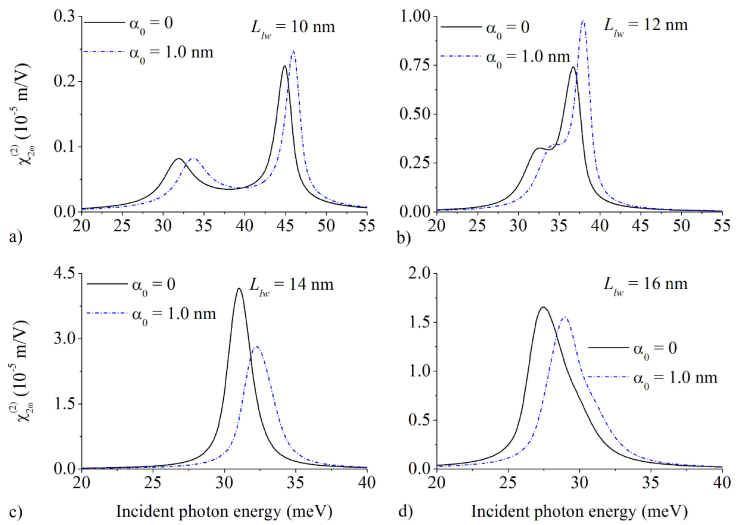
Figure 5 Second harmonic generation for the system as a function on the incident photon energy, for L lw with values of; a) 10 nm, b) 12 nm, c) 14 nm, and 16 d) nm, without ILF effect (continuous line) and with α 0 = 1 nm (point-dashed line).
Figure 6 show the effect of the in-plane external magnetic field on the SHG for the system, with the same set of parameters used in the previous figure, with α 0 = 0. In Fig. 6a), with L lw = 10 nm, the applied magnetic field, with values of 5 and 10 T, induces small changes in the shape of the SHG signal in comparison with the B = 0 situation. For L lw = 12 nm, depicted in Fig. 6b), we can see a more important diminishing in the SHG signal due to the applied magnetic field. The most interest case is given in Fig. 6c), that corresponds to L lw = 14 nm, where we can observe a quenching tendency in the SHG signal for B = 10 T, that allows to state that the SHG signal can be attenuated or even turns of by the effect of the magnetic field. Finally, when L lw reaches the value of 16 nm, as can be seen in Fig. 6d), the magnetic field importantly enhance the SHG signal, followed with a blue-shift in the SHG peak.
4. Conclusions
In this paper we report a second harmonic generation systematic study for an asymmetric Al x Ga 1-x As/GaAs QW well as a function of non-resonant intense laser field effect and an (in-plane) magnetic field. For the chosen set of parameters, without intense laser field effects and any magnetic field B, we found two energy level crossing (resonances) but only the second one, for L lw about 14 nm has large values on the dipole matrix element product ǀM 10 M 12 M 20 ǀ, that importantly enhance for L lw > 6 nm, that are fundamental for the second harmonic generation. We can conclude that the intense laser field effect, although it seems that it does not affect the dipole matrix elements so much, has noticeable blue-shift correction in the second harmonic generation signal, that importantly affect the amplitude, particularly near the energy level crossing. The most important effect on the second harmonic generation signal is due to the in-plane (x-directed) applied magnetic field because, as we can be seen from our results, this significantly affect the dipole matrix elements ǀM ij ǀ as well as the energy level structure, that have noticeable effect on the optical properties. In this paper we state that for the chosen set on parameters, that are within the experimental feasible ones, the magnetic field can be used to enhance the second harmonic generation signal or even as mechanism to inhibit this one, that can be used as a switching mechanism.











 nueva página del texto (beta)
nueva página del texto (beta)



