1. Introduction
The nonlinear partial differential equations (NPDEs) are of key importance due to their significant role in diverse disciplines of science and technology, including heat transfer, wave propagation, elasticity, fibres, condensed matter physics, fluid dynamics, hydrodynamics, and nuclear physics. The nonlinear wave structures have fascinated many researchers in the recent decades due to their numerous properties observed in numerous disciplines. In the presence of solitary waves, the nonlinear evolution models are utilized to simulate the effect of surface for deep water and weakly nonlinear dispersive long waves. Therefore, the exact solutions of such models play a vital role to study the dynamical behaviour and further properties of physical phenomenon occurring in several fields such as electromagnetism, physical chemistry, geophysics, ionised physics, elastic medium, fluid motion, fluid mechanics, elastic medium, nuclear physics, electrochemistry, optical fibres, energy physics, chemical mechanics, gravity, biostatistics, statistical and natural physics [1-7].
To investigate the behaviour of ultra-modern models, renowned researchers from all over the world are able to devise a variety of interesting numerical and analytical approaches. As a result, the study of nonlinear wave structures has latterly received a lot of attention. The Tanhcoth expansion function technique [8, 9], the sub ODE method [10, 11], the sine-Gordon technique [12-14], the first integral technique [15-17], the modified Kudryashov approach [18], the extended simplest equation method [19-21], the modified simple equation method [22-24], the Kudryashov-expansion method [25], the Lie symmetry technique [26, 27], the extended Tanh technique [28, 29], the modified Khater method [30], and the Homogeneous balance method [31, 32], are some of the key approaches which have been found in current decades.
The (3+1)-dimensional Boiti-Leon-Manna-Pempinelli (BLMP) model is an extension of the 2-dimensional BLMP model that describes the three dimensional interconnection of the Riemann travelling wave solutions along x and y-axis [33, 34], which reads
where u is a function which depends on the coordinates (x, y, z, t). Darvishi et al. studied the one wave and different numerous waves solutions for the three dimensional BLMP problem by employing different exp-function approaches [35]. Xu developed four types of lump solutions using the Painleve-Backlund transformation [36, 37], with two N exponential functions and quadratic functions. The multi-ple exponential function approaches [38, 39] and scale trans-formation approaches [40, 41] were also used to investigate the BLMP equation by Tang and Zai. Ma et al., being used to calculate the precise three-wave solutions. Exact solutions, such as periodic wave solutions, periodic solitary waves, and kink solutions can be found. Using Hirotas bilinear approach, were also generated three soliton waves results in words of kink periodic wave solutions. By employing the group trans-formation approach [42, 43], Mabrouk et al. are able to develop various appealing analytical solutions.
The basic aim of this study is to use two efficient approaches to get traveling and solitary waves solutions to the (3+1)-BLMP model namely the (F/G)-expansion technique [44] and unified technique [45, 46]. The aforementioned approaches are traveling wave solutions that can be expressed by a polynomial in (F/G) and Θ (X). Traveling and the solitary waves solutions to the dynamical model are examined physically and analytically.
2. Description of proposed methods
2.1. The new (F/G)-expansion method
Consider the NPDE in the following form
φ is an unknown function of the variables x and t and F is a polynomial in φ(x,t) and its partial derivatives, involving highest derivatives and nonlinear terms. Suppose the following transformation
where c is a non-zero constant. The travelling wave variable η allows us to reduce Eq. (2) to an ODE for φ = φ(η)
The major process of new F/G-expansion method is outlined below:
Step 1. The solution of Eq. (4) will be in (F/G) as follows,
where G = G(η) and F = F(η) satisfy
a 0, a 1, · · · , a m , λ and µ are constants to be calculated later, a m ≠ 0.
Step 2. Furthermore, N is a positive integer that can be calculated by using the homogeneous balance principle between the higher derivatives and nonlinear terms in ODE Eq.(4). We may get the following solutions of F(η) and G(η), with the help of Eq.(6), which are listed as below,
Case I. If λ > 0, μ > 0, we get the hyperbolic function solution
Case II. If λ < 0, µ < 0, we get the hyperbolic function solution
Case III. If λ > 0, µ < 0, we get the trigonometric function solution
Case IV. If λ < 0, µ > 0, we get the trigonometric function solution
Step 3. Putting Eq. (5) and Eq. (6) into Eq. (4) a group of algebraic equations for(F/G) i (i = 1, 2, . . . , m) is obtained. Setting all (F/G) i to zero and solving these nonlinear algebraic equations we get different accurate solutions of Eq. (2) according to (3), (5), (7), (8) and (9), (10).
2.2 The unified method
The major process of unified method is outlined below,
Step 1. The solution of Eq. (4) is then assumed and may be written as follows,
where A i , B i (i = 0, 1, ......, N) are constants to be determined, N is a possitive integer and Θ(X) satisfies the Riccati differential equation,
where Θ’ = dΘ/dX and γ is a real constant. Equation (12) has the following exact solutions.
Family 1. If γ < 0, then
Family 2. If γ > 0, then
Family 3. If γ = 0, then
where A, B and η 0 are real arbitrary constants.
Step 2. The positive integer N in Eq. (11) can be determined by homogeneous balance principle between the higher derivatives and nonlinear terms in ODE Eq. (4).
Step 3. Putting Eq. (11) along with Eq. (12) into Eq. (4) and setting the coefficients of Θ i (i = 0, ±1, ±2, ...) to zero, we get the system of equations.
Step 4. After solving the system of algebraic equations, we substitute the obtained constants together with the solution of Eq. (12) into Eq. (11) to obtain exact solutions of Eq. (2).
3. Soliton structures
3.1 Application to the new (F/G)-expansion approach
Consider the wave transformation
where λ, µ, ν and κ are constants. Substituting values from Eq. (16) to Eq. (1). We obtain the following ordinary differential equation,
By using the homogeneous balance principle we obtain N = 1.
The solution of Eq. (17) has the form
Putting Eq. (18) into Eq. (17), collecting all same powers terms of (F/G) together, and setting each (F/G) polynomial to zero yields the following group of algebraic system of equations
Solving the above algebraic problem results in the values
Substituting the above results into Eq. (18), produces the following four categories of traveling wave solutions.
Family I.
Case I. When λ > 0, µ > 0, we get the hyperbolic function solution
where X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants. If C 1 = 0, then we obtain the solitary wave solution
Case II. When λ < 0, µ < 0, we get the hyperbolic function solution
where
And X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants. If C 1 = 0, then we obtain the solitary wave solution
Case III. When λ > 0, µ < 0, we get the trigonometric function solution
where
and X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants. If C 1 = 0, then we obtain the solitary wave solution
Case IV. When λ < 0, µ > 0, we get the trigonometric function solution
where
and X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants. If C 1 = 0, then we obtain the solitary wave solution
Family II
Substituting the above results into Eq. (18), produces the following four categories of traveling wave solutions.
Case I. When λ > 0, µ > 0, we get the hyperbolic function solution
where
and X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants. If C 1 = 0, then we obtain the solitary wave solution.
Case II. When λ < 0, µ < 0, we get the hyperbolic function solution
where
And X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants.
If C 1 = 0, then we obtain the solitary wave solution
Case III. When λ > 0, µ < 0,we get the trigonometric function solution
where X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants. If C 1 = 0, then we obtain the solitary wave solution
Case IV. When λ < 0, µ > 0, we get the trigonometric function solution
where X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants.
If C 1 = 0, then we obtain the solitary wave solution
Family III.
Substituting the above results into Eq. (18), produces the following four categories of traveling wave solutions.
Case I. When λ > 0, µ > 0, we get the hyperbolic function solution.
where
and X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants.
If C 1 = 0, then we obtain the solitary wave solution
Case II. When λ < 0, µ < 0, we get the hyperbolic function solution.
where
and X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants.
If C 1 = 0, then we obtain the solitary wave solution
Case III. When λ > 0, µ < 0, we get the trignomatric function solution
where
and X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants.
If C 1 = 0, then we obtain the solitary wave solution
Case IV. When λ < 0, µ > 0, we get the trignomatric function solution
where
and X = νt + κx + µy + λz, C 1 and C 2 are arbitrary constants.
If C 1 = 0, then we get the solitary wave solution
4. Application to the unified method
By using the homogeneous balance principle we obtain
Putting Eq. (43) into Eq. (17), collecting all same powers terms of Θ i together and setting the coefficients of Θ i (i = 0, ±1, ±2, ...) to zero, we get the system of equations
Solving the above algebraic problem, the following are the outcomes:
Family I.
Putting above results into Eq. (43), produces following categories of traveling wave solutions.
Case I. When γ < 0, we get the solution
where
where
and
Case II. When γ > 0, we get the solution
where
where
Case III. When γ = 0, then we get the solution.
where
Family II.
Putting the above results into Eq. (43), produces following four categories of traveling wave solutions.
Case I. When γ < 0, we get the solution
where
where
Case II. When γ > 0, we get the solution
where
Case III. When γ = 0, then we get the solution
where
Family III.
Putting the above results into Eq. (43), produces following four categories of traveling wave solutions.
Case I. When γ < 0, we get the solution
where
where
Case II. When γ > 0, we get the solution
where
where
Case III. When γ = 0, then we get the solution
where
Family IV.
Putting the above results into Eq. (43), produces following four categories of traveling wave solutions.
Case I. When γ < 0, we get the solution
where
Case II. When γ > 0, we get the solution
where
Case III. When γ = 0, then we get the solution
where
5. Discussion and results
This section contains the graphical depictions of optical solitons and periodic wave structures. A family of periodic and solitary wave solitons are shown for a given set of values. In this section, the graphical representation of exact solution of (3+1)-BLMP model has been illustrated. Soliton solutions, dark solitons, single soliton, periodic type solitons, bell shaped solitons, singular solitons, as well as various Boiti-Leon-Manna-Pempinelli soliton solutions are obtained in various forms. The new (F/G)-expansion method and the unified method is applied to get the exact traveling wave solutions for the set of values. The 3D, contour and 2D graphs visualize the nature of nonlinear waves constructed from Eq. (1).
6. Conclusion
In this study, we have found a large number of exact solutions to the higher-dimensional Boiti-Leon-Manna-Pempinelli model which plays a significant role to describe numerous dynamical phenomenon in diverse disciplines of science and engineering such as chemical physics, particle physics, quantum field theory, optical fibers, fluid dynamics, hydrodynamics. Exact traveling wave solutions always provide a complete account of dynamical behaviour of the most complicated physical phenomena that have yet to be researched. A set of state-of-the-art analytical techniques namely the new (F/G)-expansion method and the unified method are employed to develop numerous solitary and traveling wave solutions such as the bright solitons, dark solitons, single soliton, periodic type solitons, bell shaped solitons, hyperbolic and trigonometric functions, for details see Figs. 1-12. We are able to achieve distinct graphical interpretations to the nonlinear wave structures for the suitable choice of parameters. The contemplated results confirm that the applied techniques are powerful and efficient for obtaining analytical solutions to a variety of nonlinear problems emerging in the contemporary era of ocean engineering and wave motion. In future, other methodologies and nonlinearity laws may be used to explore such model, thus there is still a lot of fresh work to be done on it.
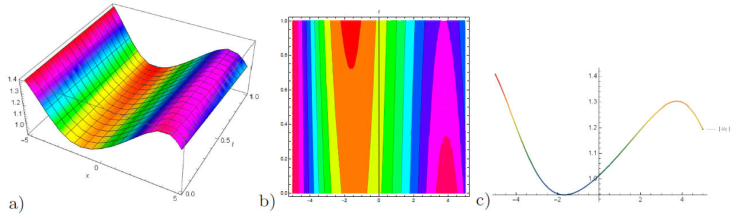
Figure 1 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 1(x, y, z, t) for the values of λ = 0.5, μ = 0.1, and v = -0.4, y = 1.
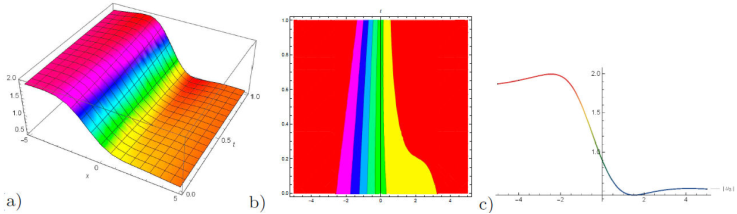
Figure 2 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 3(x, y, z, t) for the values of λ = 0.3, μ = -0.9, and v = 0.7, y = 1.
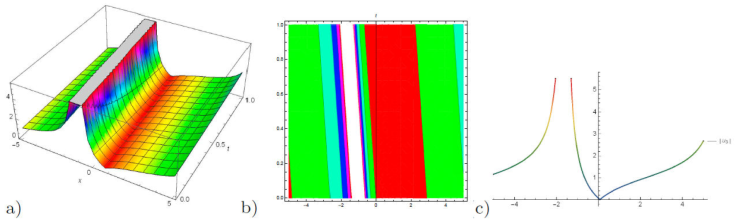
Figure 3 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 7(x, y, z, t) for the values of λ = 0.1, μ = -2.9, and v = 0.5, y = 1.
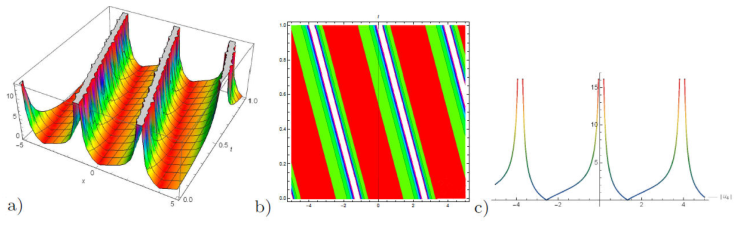
Figure 4 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 8(x, y, z, t) for the values of λ = -1.1, μ = 2.1, and v = 1.4, y = 1.
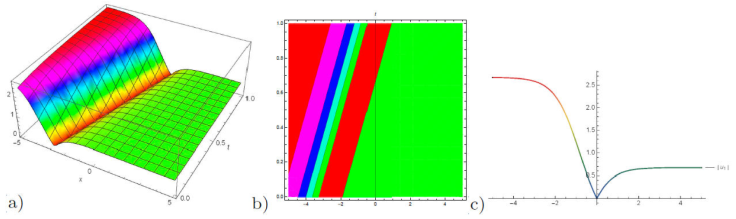
Figure 5 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 9(x, y, z, t) for the values of λ = 1.5, μ = 0.5, and v = -2.7, t = 1, y = 1.
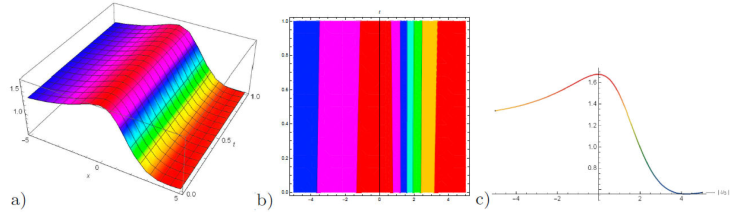
Figure 6 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 11(x, y, z, t) for the values of λ = 1.05, μ = -0.09, and v = -0.05, y = 1, t = 1.
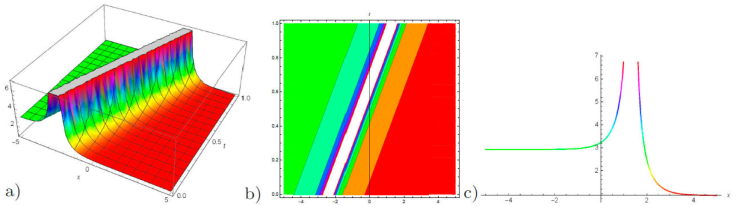
Figure 7 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 13(x, y, z, t) for the values of λ = 1, μ = 0.4, γ = -2.2, κ = -2, and v = 1.2, A = 2, A 0 = 1, η 0 = 1, z = -2, B = -1, y = 1, t = 1.
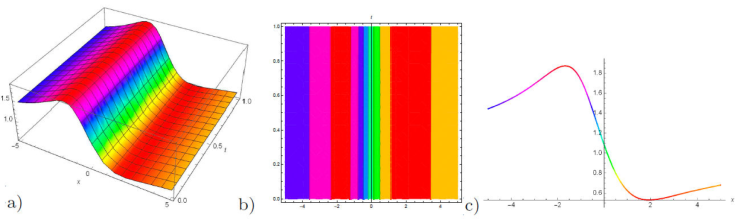
Figure 8 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 15(x, y, z, t) for the values of λ = -0.2, μ = 1.2, γ = 0.02, κ = 2, and v = -0.003, A = -1.02, B = -0.5, A 0 = 1, η 0 = 1, z = 0.1 = y = 1, t = 1.
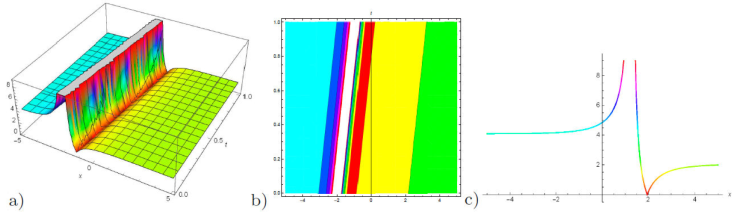
Figure 9 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 19(x, y, z, t) for the values of λ = -0.2, μ = 1, η 0 = 1, z = 1, γ = -0.3, κ = -1, and v = -1, A = -1, A 0 = 1, B = -0.3, y = 1, t = 1.
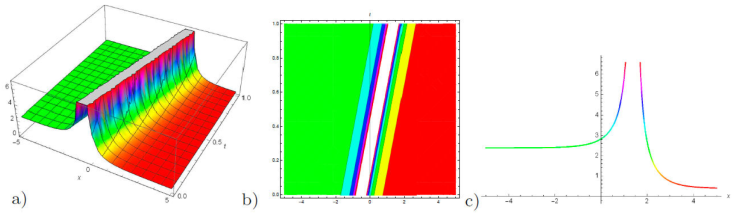
Figure 10 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 23(x, y, z, t) for the values of λ = -0.2, μ = 1, η 0 = 1, z = 1, γ = -0.3, κ = -1, and v = -1, A = -1, A 0 = 1, B = -0.3, y = 1, t = 3.
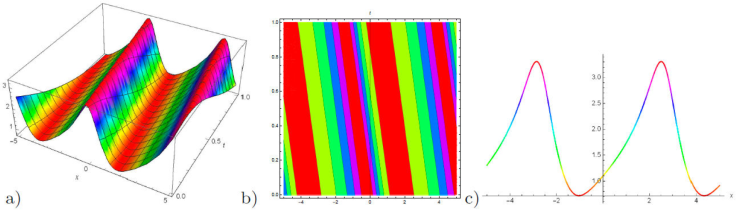
Figure 11 a) 3D plot, b) contour plot and c) 2D plot for the solution of u 25(x, y, z, t) for the values of λ = 0.2, μ = -1, η 0 = 1, z = -2, γ = 4, κ = -1.2, and v = 0.2, A = -1.2, A 0 = 1, B = 1.3, y = 1, t = 2.











 nueva página del texto (beta)
nueva página del texto (beta)



