1. Introduction
Heusler alloys were discovered in 1903 by Fritz Heusler, they are gaining more and more attention from researchers [1]. Full and Half-Heusler alloys have a broad family of multi-functional materials for spintronic compound [2-8], shape memory alloys [9], superconducting ground state [10], and thermoelectric materials [11], Heusler alloys have Slater-Pauling behavior [12], higher curie temperature [13-15], Heusler’s alloys are important materials in terms of their interesting properties such as electronic localization, itinerant magnetism, antiferromagnetism, helimagnetism, Pauli paramagnetism or the behavior of heavy fermions [16], Many researchers have discovered some full-Heusler alloys are not half-metals, but they present a metallic character because of the metallic nature of their spin-polarized electronic structures [17-20]. Among full-Heusler alloys, the Rh2CrGe [17] and Rh2MnTi alloys [18] which showed the metallic character, due to overlap between valence bands and conduction bands at the Fermi level with the two spins channels. While other researchers have shown that the metallic character of certain compounds products from the contribution of Rh, and (Cr,Mn)-3d states around the Fermi level [17,18]. The regular Heusler compounds X2YZ, with 2:1:1 stoichiometry, crystallize in the cubic L21 structure (
2 Calculation details
Electronic structure calculations of our full-Heusler compounds were performed using the first-principle calculations of density functional theory [24,25] based on the FP(L)APW method is implemented in the Wien2k code [26-29]. For exchange-correlation potential, we used the local density approximation (LDA) proposed by Perdew and Wang [30], and the GGA-PBE approximation proposed by JP. Perdew, K. Burke, and M. Ernzerhof [31]. It calculates the self -consistent solution of the equations of Kohn and Sham [25]. In these calculations, we have chosen the values of the radii of the atoms of Os, Ti, Sc, V and Al of 2.2, 2, 2, 2.1 and 2 u.a, respectively, so that there is no overlap Muffin-Tin spheres. The electronic configurations of the sets of the system studied are: Os (6s24f145d3), Ti (3d2 4s2), Sc (3d1 4s2), V (3d3 4s2), and Al (3s2 3p1). We have used a 1500K-point Monkhorst-Pack mesh [32,33] in the Brillouin zone for all compounds. We chose the RMT × Kmax = 7 (where RMT is the mean radius of muffin-tin spheres). The energy cutoff was chosen as -6 Ry, used for separation between the valence and the core states. The basic functions and potentials are extended in combinations of spherical harmonics around atomic sites, that is to say, the atomic spheres with a cutoff of Imax = 10, and in Fourier series in the interstitial. The self-consistent convergence of the total energy was set at 0.1 mRy.
3 Results and discussion
3.1 Structural properties
The compounds Os2YA1, (Y=Sc, Ti, and V), as most “Full Heusler" alloys crystallize in type structure “regular” (Cu2 MnAl, L21 prototype) with space group
where E0 is the minimum energy at T = 0 K, B is the bulk modulus, B’ is the bulk modulus derivative and V0 is the equilibrium volume, all the points are effectuated by using the LDA approximation [30]. The optimized lattice parameter is almost the same as what has already been reported [34,36,37]. The results concerning the optimization of three materials Os2YAl, (Y=Sc, Ti, V), (lattice parameters, the compressibility modulus, and their derivatives, and the equilibrium energies, optimized with the LDA and PBE), are grouped in Table I. The calculated lattice equilibrium constant values (a0) of the Os2YAl compounds (y = Sc, Ti, and V) are compared to the lattice parameters available in the literature which are very close to each other [34,36,37]. The lattice constants for Os2ScAl, Os2TiAl, and Os2VAl differs by a percentage of approximately 1.83%, 1.8%, and 1.53%, respectively using LDA approximation, for PBE approach the results are improved. No experimental data were found for the lattice parameters of the compounds Os2TiAl and Os2VAl for comparison. The mass modulus calculated for the material Os2ScAl is closer to the available results [34]. For the mass modulus of the compounds Os2TiAl and Os2VAl, no experimental value was found for comparison.
Table I Calculated equilibrium lattice constants a(Å), bulk modulus B0 (GPa), and its first derivative B’, Equilibrium Energy, and the valence electron concentration (val-el), of Os2YAl (Y=Sc, Ti and V)
| a(Å) | B0(GPa) | B’ | Ech(eV/atom) | Efermi | E (Ry) | Method | |
|---|---|---|---|---|---|---|---|
| Os2ScAl | 6.13 | 222.57 | 4.31 | -2.605 | 0.88 | -71097.499 | LDA |
| 6.21 | 193.31 | 4.44 | -71152.061 | PBE | |||
| Previous [36] | 6.244 | ||||||
| [34] | 6.268 | 194.26 | |||||
| [37] | 6.239 | ||||||
| Os2TiAl | 6.01 | 273 | 4.24 | -2.614 | 0.92 | -71276.567 | LDA |
| 6.09 | 233.82 | 4.84 | -71321.322 | PBE | |||
| Previous [36] | 6.12 | ||||||
| Os2VAl | 5.94 | 307.4 | 4.23 | -2.931 | 0.99 | -71467.353 | LDA |
| 6.01 | 260.98 | 4.92 | -71512.273 | PBE | |||
| Previous [36] | 6.032 |
We can say that the Os2VAl compound has a higher negative energy and harder than Os2ScAl, and Os2TiAl compounds due to the large value of the compressibility module. We note that when we go to an increased Sc-Ti-V and fixing X = Os and Z = Al, the mass modulus of X2YZ increases.
3.2 Formation and cohesive energy
To confirm the structural stability we calculated the cohesion energy and the energies of the individual atoms by increasing the unit cell of a face-centered cubic structure [39] up to 30 Bohr (about 16 Å) for the three compounds. The cohesion energy
Y =Sc, Ti, and V with
The cohesive energies are also indicated in Table I. It is found that the cohesion energy of the Os2ScAl, Os2TiAl and Os2VAl compounds are -2.605 eV / atom, -2.614 eV/atom, and -2.931 eV/atom, respectively. From these results, we can say that the compound Os2VA has high stability compared to the compounds Os2ScAl and Os2TiAl, and the Os2TiAl compound is more stable than the Os2ScAl compound. These results are comparable to the results of the optimization part.
3.3.1 Band structures
Figures 3, 4 and 5, show the band structure of the studied systems Os2YAl, (Y=Sc, Ti, V) with LDA, TB-mBJ [41-44], and LDA+SOC, respectively, calculated at their equilibrium lattice constants at different high points of symmetry in the Brillouin zone. The valence bands pass through the Fermi level and enter the conduction band for all structures, but do not overlap except Os2VAl for the three approximations, and the absence of a forbidden band which clearly indicates the metallic character. The dispersed upper bands are due to the strong hybridization of the (d) states of (Os, and Ti, Sc, and V). These results are similar to other results of the same family [34].
3.3.2 Densities of states
The projected total and partial state densities (DOST) (DOSP), between -18.5 and 9 are illustrated, respectively, in Figs. 4a), b), c), and the Fermi level is taken as the origin of the energies. The analysis of the figures of the total and partial state density of the Os2ScAl, Os2TiAl, and Os2VAl indicates a non-zero density at the Fermi level and the absence of the forbidden band Eg which makes it possible to deduce that these materials have a metallic nature, (since the DOS has a great value at the Fermi level, see Table I). At the Fermi level, the DOS is 47.6, 34, and 13.6 states per cell unit per eV, respectively for Os2ScAl, Os2TiAl, and Os2VAl. Therefore, there is a downward disposition concluded which makes Os2ScAl more conductive than Os2TiAl and Os2VAl. We find that the TDOS around the Fermi level come mainly from electrons (Ti-d), and (Os-d) the states (p) of the (Al) elements occupy the lowest part of the valence states and have a small contribution around the Fermi level. In addition, there are two atoms of (Os), and only one atom of (Sc, Ti, and V) but the contribution of the Sc, Ti and V atoms is less efficient compared to the Os atom. The hybridization between the states Os (d), Y (d), and Al (p) becomes stronger when the lattice parameter increases with the atomic number of the elements (Y = Sc, Ti, and V). We can also see that the partial DOS of Y=Sc, Ti, and V (3d) orbitals in three materials exhibit the same behavior.
3.4 Elastic properties and mechanical stability
Furthermore, we have also considered to mechanical properties of the Os2YAl (Y=Sc, Ti, and V) full-Heusler alloy. The elastic properties describe the mechanical behavior of materials, their study is also important for the field of engineering. Knowledge of the elastic properties of materials is important for fundamental research, particularly for understanding the mechanisms of the bonds between atoms. The cubic structure materials have three independent elastic constants: C11, C12, and C44. To obtain the elastic constants for these compounds, we used a first-principles numerical calculation using the method developed by Reshak and Morteza and integrated into the WIEN2k code [45]. From Table II, one can say that the Os2TiAl, Os2ScAl, and Os2VAl compounds are mechanically stable because all these elastic constants are positive and meet the criterion of mechanical stability verify the relation in (3) [46-49],
Table II Elastic constant Cij, and the anisotropic factors for the Os2YAl (Y=Sc, Ti and V).
| C11 (GPa) | C12(GPa) | C44(GPa) | A | Cp = C12 - C 44 | |
|---|---|---|---|---|---|
| Os2ScAl | 308.73 | 181.67 | 98.73 | 1.55 | 82.94 |
| Previous [34] | 261.908 | 160.436 | 102.312 | 2.016 | 58.124 |
| Os2TiAl | 401.16 | 205.15 | 158.1 | 1.61 | 47.05 |
| Os2VAl | 516.9 | 202.98 | 163.6 | 1.04 | 39.38 |
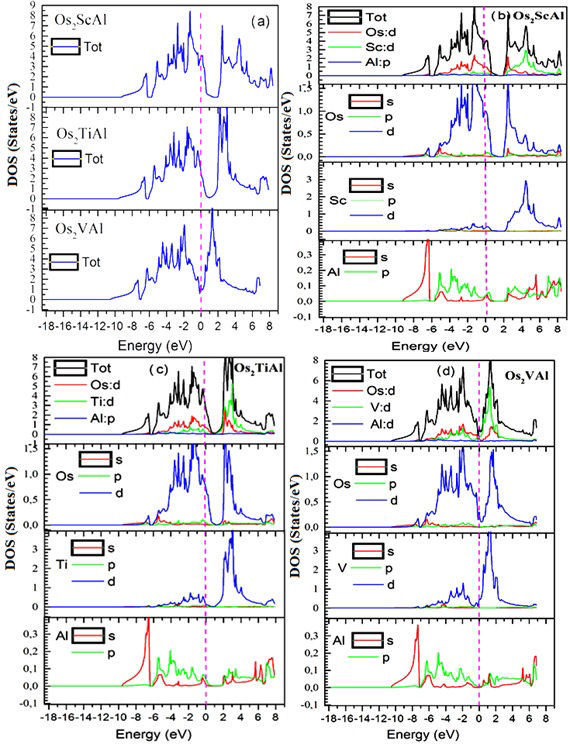
Figure 6 Total a) and partial density of states of Os2ScAl b), Os2TiAl c), Os2VAl d). The Fermi level is set to zero energy and marked by a vertical dashed line.
Our results show that the value of the C11 constant is larger than the other constants for three compounds. So, we can say that the length change resistance is the most important in these compounds. The Cij modules have a heavyweight in the study of materials especially the C44 module, from this module, can determine several properties such as fragility, among others. The C44 module shows that Os2VAl is harder than Os2 TiAl, and Os2ScAl; this result is similar to the one found in the optimization part. The elastic constants obtained for the compound Os2ScAl are in good agreement with the available results, whereas the values of C11 are greater than those reported in [34]. The value of C44 was lower than the search result [34]. For the compounds Os2TiAl, and Os2VAl, no results were found for comparison. By comparing the C11 values of the compounds studied, we verified that its values are of the increasing order according to the increase in the atomic number of the element Y = Sc, Ti, and V. According to Pettifor [50,51], the character of atomic bonding in metals and compounds, also relates to the brittle or ductile characteristics can be found by considering the Cauchy pressure (CP). A negative value of CP shows a strong covalent bond while a positive value of CP indicates a strong metallic bond. The Cauchy pressure values are 82.94 GPa, 47.05 GPa, and 39.38 GPa for Os2ScAl, Os2TiAl, and Os2Val, respectively. The obtained values for the pressure are all positive, showing a metallic character and ductile nature of the compounds. These results confirm the metallic bonding character of the three materials, and the most stable compound was Os2VA1, in agreement with the optimization and cohesive energy calculations, as well as the electronic band structure analysis.
The knowledge of the elastic constants Cij allows us to calculate other mechanical (elastic) quantities such as the modulus of compressibility B, the Young and shear modulus (Y and G), as well as the Poisson’s ratio (v) which are important parameters in technological applications and provide a fundamental description of the mechanical behavior of a material. The bulk modulus is used to measure the hardness of materials to volume variation by the applied hydrostatic pressure [47,48], while the shear modulus G represents the resistance to plastic deformation and gives the behavior of a material under a uniform pressure [47-49]. For a cubic crystal the bulk modulus B, the Voight-Reuss-Hill averaged shear modulus G, Poisson’s ratio v, and Young’s modulus are expressed as follows [35,36,38,46-48,52-54].
The Reuss bounds [46,55] of the bulk and shear modulus are BV = BR and
According to the Hill approximation [46,56] method, arithmetic mean of the Voigt and Reuss’s shear moduli gives the elastic modulus expressed as following:
where GV is the Voigt shear modulus and GR is the Reuss shear modulus.
The mass modulus (B) is greater than the shear modulus (G) for all three compounds. Thus, these materials must be resistant to changes in their volumes under uniform pressure. The results of the modulus of mass B obtained as a function of the elastic constants are of the same order as the results obtained by applying the Murnaghan equation [38], displaying that our estimated results of the elastic constants for Os2ScAl, Os2TiAl, and Os2VAl are exact and precise. The Young’s modulus E and Poisson’s ratio v for a cubic structure are related to the modulus of compressibility B and shear G. Using the relation [36,46-48],
The Young’s modulus is defined as the ratio between stress and strain and is used to provide a measure of the stiffness of the solid matter, i.e., the larger the value of E, entails a stiffer material [46,57]. We can see from the results mentioned in Table III, that the Young’s modulus value E is in ascending order, and Os2VAl compound is more rigid and harder than Os2ScAl and, Os2TiAl due to its higher value of Young’s modulus, and compressibility modulus (B). At the same time, the value of E of compound Os2ScAl is of the same order of results available [34].
Table III The bulk modulus B, shear modulus G, Young’s modulus E Poisson’s ratio v, and the bulk-modulus -to- shear-modulus ratio, for the Os2YAl (Y=Sc, Ti and V).
| E(GPa) | B (GPa) | G (GPa) | v | B/G | |
|---|---|---|---|---|---|
| Os2ScAl | 220.99 | 224.02 | 82.735 | 0.32 | 2.70 |
| Previous [34] | 214.922 | 194.260 | 81.681 | 0.31 | 2.398 |
| Os2TiAl | 337.280 | 270.48 | 130.51 | 0.29 | 2.07 |
| Os2VAl | 411.04 | 307.61 | 160.9 | 0.27 | 1.90 |
Table IV Calculated total and local magnetic moments per atom unit cell (in units of the Bohr magneton μB), and in the interstitial sites for Os2YAl, Y = Sc, Ti, and V.
With an increase in Poisson’s ratio, the plasticity of the crystal improves. The Poisson’s ratio has been suggested as 0.1 for covalent substances and 0.25 for ionic substances in the literature [17,58]. The Poisson ratios for the alloys Os2ScAl, Os2TiAl, and Os2VAl are, respectively, 0.32, 0.29, and 0.27, (see Table III) which means that the alloys have a metallic ionic reaction. For an isotopic crystal A = (2C44)/(C11-C12) is equal to 1, but when there is another value greater or less than 1 it means that it is an anisotropic crystal [59,60]. According to Table II, the anisotropy coefficient exceeded unity, which indicates that our compounds have an anisotropic character. The Pugh criterion [59,61], is the ratio between the compressibility modulus and the shear modulus (B/G) of the polycrystalline phases could also be used as a measure to quantify whether a material breaks in a ductile or brittle manner. Subsequently, a high (low) value of this ratio is associated with ductility (brittleness). The critical value separating the ductile and the brittle turned out to be 1.75. As shown in Table III, this ratio is greater than 1.75 for the three Os2ScAl, Os2TiAl, and Os2VAl compounds, which are classified as ductile compounds, and this result confirmed previous data [34].
4 Conclusion
In summary, we have studied the structural, elastic, and electronic properties of the Heusler Os2YAl,(Y=Sc, Ti, V) alloy, with the space group











 nueva página del texto (beta)
nueva página del texto (beta)








