Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería sísmica
versión impresa ISSN 0185-092X
Ing. sísm no.84 Ciudad de México ene./jun. 2011
Artículo
Estimación de propiedades dinámicas de arcillas
Claudia M. González Blandón1 y Miguel P. Romo Organista1
1 Instituto de Ingeniería, UNAM, Coordinación de Geotecnia. Circuito Escolar, Ciudad Universitaria, Coyoacán, 04510, México D.F. cgonzalezb@ii.unam.mx, mromo@pumas.iingen.unam.mx
Recibido el 31 de agosto de 2010
Aprobado el 5 de febrero de 2011
Resumen
Se propone un procedimiento de modelación tipo Masing, para estimar los comportamientos no lineales de propiedades dinámicas de arcillas normalmente consolidadas. Estos comportamientos corresponden a las variaciones del módulo de rigidez al corte y de la relación de amortiguamiento respecto a la deformación angular. El procedimiento es producto de un análisis minucioso de las propuestas realizadas por Romo (1990, 1995) y Flores et al. (1999). Dicho análisis sustenta la necesidad de definir valores de la deformación de referencia y del parámetro B, para cada una de las propiedades dinámicas. Por ende, se puede concluir que la modelación del módulo de rigidez y de la relación de amortiguamiento, se debe realizar de manera independiente. Finalmente, se ilustra el procedimiento de modelación mediante un ejercicio de aplicación, en el que se obtienen las curvas G - γ y λ - γ de una muestra de arcilla de la Ciudad de México.
Palabras clave: Masing; arcilla; índice de plasticidad; módulo de rigidez al corte; relación de amortiguamiento.
Abstract
A modeling procedure based on Masing rules is proposed to estimate the nonlinear dynamic behavior of normally consolidated clays. The properties we are concerned in this paper are the shear modulus and the damping ratio. The procedure is the product of a careful analysis of the models proposed by Romo (1990, 1995) and Flores et al. (1999). This analysis supports the need to define values of the reference strain and of the parameter B, for each one of the dynamic properties. Therefore, it is concluded that the modeling of shear modulus and damping ratio should be carried out independently. Finally, the modeling procedure through an application exercise is presented. In this exercise, the G - γ and λ - γ curves of a clay sample from Mexico City are obtained.
Key words: Masing; clay; plasticity index; shear modulus; damping ratio.
Introducción
Para evaluar la respuesta dinámica de un depósito de suelo y de sistemas suelo-estructura, es necesario conocer propiedades del material en cuestión, como el módulo de rigidez al esfuerzo cortante, G, y la relación de amortiguamiento, λ. Estas propiedades presentan comportamientos no lineales respecto a la deformación angular, γ. La obtención experimental de estas propiedades, frecuentemente, es afectada por la disponibilidad de equipos necesarios y los costos de las pruebas requeridas. Por tal razón, se recurre a procesos de modelación que requieren un mínimo de pruebas experimentales y facilitan los análisis.
A la fecha existen modelos (Seed e Idriss, 1970; Hardin y Drnevich, 1972; Ramberg-Osgood, 1970 (descrito por Anderson y Richart, 1976); Romo, 1995; Flores et al., 1999) que consideran, según el tipo de suelo, tendencias en los comportamientos de las propiedades dinámicas. Por ejemplo, en arcilla de la Ciudad de México, para niveles de deformación angular menores o iguales a 10−4 %, el G y la λ permanecen prácticamente constantes; por consiguiente, para γ iguales o inferiores a 10−4 %, se asume que los valores del G y de la λ corresponden a las magnitudes máxima del módulo de rigidez al corte, Gmax, y mínima de la relación de amortiguamiento crítico, λmín. Para deformaciones angulares superiores a este umbral (γ = 10−4 %), G disminuye hasta un valor mínimo, Gmín, cercano a cero, y λ aumenta hasta llegar a un valor máximo, λmáx, prácticamente constante.
Las expresiones propuestas por Romo (1990, 1995) y Flores et al. (1999) para la modelación del módulo de rígidez al esfuerzo cortante y la relación de amortiguamiento de suelos son, hasta la fecha, utilizadas para evaluar el comportamiento dinámico de diversos materiales (e.g. González et al., 2007; Ossa y Romo, 2008). Este documento presenta un análisis paramétrico de dichas expresiones, considerando las hipótesis adoptadas en el planteamiento de las mismas. Finalmente, se propone un modelo modificado tipo Masing para obtener comportamientos no lineales del G y de la λ de arcillas normalmente consolidadas.
Modelo tipo masing
La modelación de las propiedades dinámicas de un suelo, debe considerar una ley constitutiva que defina el comportamiento elástico (rango de pequeñas deformaciones) y elasto-plástico (rango de grandes deformaciones) de los suelos, tal como lo hace la conocida Regla de Masing (Ishihara, 1996).
Manteniendo dicha regla, Romo (1990, 1995) y Flores et al. (1999) propusieron un Modelo tipo Masing, para modelar las relaciones no lineales G-γ y λ-γ, cuyas hipótesis son:
- El material sometido a carga armónica con amplitud constante responde de manera estable, si el amortiguamiento histerético es suficiente para atenuar en pocos ciclos la parte transitoria.
- La no linealidad del material es de naturaleza plástica, es decir, la rigidez del suelo regresa a su valor máximo cada vez que la carga cambia de sentido.
- El amortiguamiento es de tipo histerético.
Las expresiones que estos autores propusieron son:
 (1)
(1)
 (2)
(2)
 (3)
(3)
donde: Gmáx y λmín corresponden a los valores del G y de la λ para el rango de deformaciones, en el cual el comportamiento del suelo es elástico (figura 1); Gmín y λmáx son los valores del G y de la λ, mínimo y máximo respectivamente, alcanzados por el suelo antes de llegar a la falla bajo carga dinámica (figura 1); γr es una deformación de referencia, correspondiente al 50% de degradación del G (figura 1); A y B son parámetros del suelo que definen la geometría de las curvas G-γ y λ-γ y dependen principalmente del índice de plasticidad, IP.

Las condiciones de frontera (valores extremos) establecidas en las expresiones anteriores, satisfacen los siguientes límites de comportamiento de un suelo:
- Cuando γ tiende a infinito: H(γ) tiende a uno, esto implica que G tienda a Gmín y λ tienda a λmáx.
- Cuando γ tiende a cero: H(γ) tiende a cero, esto conduce a que G tienda a Gmáx y λ tienda a λmín.
Análisis de los parámetros del modelo tipo masing
A continuación se presenta un análisis paramétrico del Modelo tipo Masing.
Parámetros A y B
Los valores de los parámetros A y B son primordiales en los análisis de amplificación dinámica e interacción suelo-estructura; además, son éstos quienes dan la forma particular de las curvas módulo de rigidez versus deformación angular y relación de amortiguamiento crítico versus deformación angular.
Parámetro A
Para obtener el valor de A basta con manipular la ecuación 1, tomando en cuenta que al 50% de degradación del módulo de rígidez al esfuerzo cortante, G50, la deformación angular γ corresponde a γr. Entonces,
 (4)
(4)
Igualando G50 (expresión anterior) y la ecuación 1, se tiene
 (5)
(5)
Despejando la función H(γ) de la expresión anterior, combinando la ecuación 3 y tomando γ =γr, se tiene
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
Finalmente, al obtener el valor de A constante, se demuestra que este parámetro es independiente del índice de plasticidad. Este hecho difiere del planteamiento del Modelo tipo Masing. Cabe mencionar que aplicando un procedimiento algebraico similar con la relación de amortiguamiento crítico (ecuación 2), se obtiene el mismo resultado (A = 1).
Parámetro B
Conocido el valor de A es posible despejar B de la ecuación 7, llegando a
 (10)
(10)
De la expresión anterior se concluye que B puede tomar diversos valores. Esta variabilidad de B puede atribuirse, posiblemente, a la estructura característica del material modelado. Para el caso de las arcillas, B dependerá del índice de plasticidad, IP.
Deformación γr
La deformación γr (definida de manera arbitraria) representa la deformación correspondiente al punto de inflexión de la curva G/Gmáx-γ y por consiguiente, a los cambios de curvatura de las relaciones no lineales G-γ y λ-γ (figura 2a).

Para comprobar de manera analítica que γr corresponde al punto de inflexión de las relaciones G-γ y λ-γ, se emplea el criterio de la segunda derivada. Previamente, es necesario realizar un mapeo o transformación de abscisas, ya que dicho punto es visible en escala semi-logarítmica y no en escala aritmética (figura 2b).
El mapeo se realiza empleando la siguiente expresión
 (11)
(11)
donde t son los valores transformados de las abscisas, n es el exponente menor del rango de deformaciones manejado en escala logarítmica, a es el número de unidades por ciclo y x es la relación entre deformaciones γ/γr.
Despejando x de la expresión anterior se obtiene
 (12)
(12)
Para aplicar el criterio de la segunda derivada, es preciso partir de la ecuación 1 normalizada y expresada en función de x.
 (13)
(13)
Haciendo uso de la regla de la cadena, para obtener la primera derivada de la ecuación anterior, se tiene que
 (14)
(14)
Empleando nuevamente la regla de la cadena, se obtiene que la segunda derivada de la ecuación 13 es igual a
 (15)
(15)
Igualando la expresión 15 a cero y despejando el valor de x, se tiene que
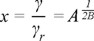 (16)
(16)
Conociendo que A = 1 y por ende x = 1, se llega a γ = γr. Ésto demuestra que el punto de inflexión de la curva normalizada del módulo de rigidez, está definido por las coordenadas (γr, (Gmáx+Gmín)/(2Gmáx)) y es independiente del valor del parámetro B. Cabe mencionar que para la relación de amortiguamiento normalizada (λ/λmáx), el seguir un procedimiento análogo al expuesto, arroja un resultado idéntico.
Demostrada la definición matemática de la deformación γr , es evidente que el Modelo tipo Masing considera un único punto de inflexión (obtenido de la relación G/Gmáx-γ) para las funciones G = f(γ) y λ = f(γ).
Sin embargo, en resultados experimentales se ha observado que los puntos de inflexión de las relaciones G-γ y λ-γ no coinciden. Normalmente, el cambio de curvatura de la relación de amortiguamiento se presenta en una deformación angular mayor que la deformación correspondiente al punto de inflexión de la relación G-γ (figura 3). Por lo tanto, se considera conveniente definir la deformación de referencia γr , tanto para la relación G-γ, γrG, como para la relación λ-γ, γrλ .

Valores Gmáx , Gmín , λmáx y λmín
Los valores máximo y mínimo de las propiedades dinámicas G y λ se definen experimentalmente y por consiguiente, son característicos y únicos del suelo que se esté modelando.
Módulo de rigidez al esfuerzo cortante
El empleo del Modelo tipo Masing parte de la función normalizada G/Gmáx=f(γ); por consiguiente, el efecto del valor máximo del G no se considera. Aunque, es de notar que tanto el Gmáx como el Gmín corresponden a valores frontera dentro del proceso de modelación. Estos valores no afectan a los demás parámetros empleados por el Modelo (figura 4).

Resultados de investigaciones experimentales concluyen que Gmáx depende fuertemente del esfuerzo efectivo de confinamiento y que Gmín , usualmente, presenta valores cercanos a cero (Romo, 1995).
Relación de amortiguamiento
De manera similar al módulo de rigidez al cortante, los valores máximo y mínimo de la relación de amortiguamiento corresponden a valores frontera dentro del proceso de modelación. Igualmente, estos valores no influyen en los parámetros A, B y γr, empleados en el Modelo (figura 4).
Modelo modificado tipo masing
Partiendo del análisis previamente descrito y con el propósito de ampliar la aplicabilidad del Modelo tipo Masing a diversas arcillas, se plantea un procedimiento de modelado nuevo. Este planteamiento conserva tanto las hipótesis como las condiciones de frontera del modelo original.
El Modelo Modificado conserva intacto el proceso de modelación de la relación no lineal G-γ . Adicionalmente, plantea un procedimiento nuevo para obtener la función λ=f(γ). Por lo anterior, los procesos de modelación de las propiedades dinámicas son totalmente independientes.
Las expresiones propuestas para el Modelo Modificado tipo Masing son:
 (17)
(17)
 (18)
(18)
 (19)
(19)
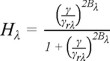 (20)
(20)
donde:
Gmáx y λmín corresponden a los valores del G y de la λ para el rango de deformaciones, en el cual el comportamiento del suelo es elástico (figura 4); estos valores son propios de cada suelo. Para las arcillas estudiadas en esta investigación (tabla 1), λmín presenta valores del orden del 0.5 al 2 por ciento para las arcillas marinas y del 1.5 al 3 por cierto para las arcillas lacustres; en el caso del Gmáx , se planteó una relación entre dicho valor, el índice de plasticidad, IP, y el esfuerzo efectivo de confinamiento, σ'c (figura 5).


Gmín y λmáx son los valores del G y de la λ , mínimo y máximo respectivamente, alcanzados por el suelo antes de llegar a la falla bajo carga dinámica. Para el caso de las arcillas estudiadas en esta investigación, Gmín y λmáx tienden a 3.5 kg/cm2 y a 17 % para las arcillas marinas y a 1 kg/cm2 y 14 % para las arcillas lacustres.
γrG y γrλ son deformaciones de referencia correspondientes al punto de inflexión de las relaciones experimentales G-γ y λ-γ ; o sea, deformaciones correspondientes al 50% de degradación del G y al 50% de aumento de la λ , respectivamente. Estas deformaciones dependen del índice de plasticidad de la arcilla en estudio: a mayor IP mayores serán las deformaciones de referencia (figura 6).

BG y Bλ son constantes que definen la geometría característica de las curvas G-γ y λ-γ , respectivamente. Al igual que las deformaciones de referencia, los valores de las constantes BG y Bλ dependen del índice de plasticidad, IP, (figura 7).

El Modelo Modificado corresponde a un procedimiento de estimación de las propiedades dinámicas de arcillas normalmente consolidadas. Para este caso, los parámetros B y γr son función del índice de plasticidad. Además, cabe destacar que este Modelo Modificado es aplicable a todo material con comportamiento elasto-plástico (Regla de Masing), donde los parámetros B y γr sean funciones de propiedades preponderantes en la estructura característica del material en estudio (e.g. materiales granulares, con parámetros B y γr como funciones de la consistencia relativa).
Validación del modelo modificado
Para evaluar la confiabilidad del Modelo Modificado se presentan resultados experimentales y teóricos de las propiedades dinámicas de dos materiales. Estos materiales presentan procesos de formación distintos y por ende, diferencias notables de estructura y de índices de plasticidad (tabla 2). Adicionalmente, el anexo contiene un ejercicio de aplicación que también permite validar la efectividad del modelo propuesto.
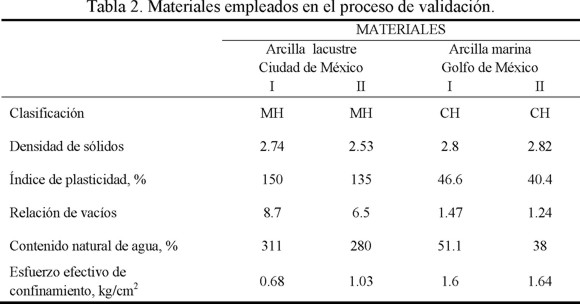
Las figuras 8 y 9 muestran algunos de los resultados experimentales, obtenidos de pruebas dinámicas realizadas en columna resonante y en cámara triaxial cíclica. También, presentan resultados teóricos producto de la aplicación del Modelo Modificado. En estas figuras se aprecia la gran proximidad de las estimaciones a los datos experimentales, tanto para el módulo de rigidez al esfuerzo cortante como para la relación de amortiguamiento, de las arcillas en cuestión (tabla 2).


La calidad de un proceso de modelación está directamente ligada a la confiabilidad con la que son determinadas las variables que influyen en dicho proceso, la cual se ve reflejada de cierta manera en el coeficiente de correlación (Hildebrand y Ott, 1998). En esta investigación, con la aplicación del Modelo Modificado, se obtuvieron relaciones teóricas G-γ y λ-γ con coeficientes de correlación, normalmente, superiores a 0.95 y en la gran mayoría valores arriba de 0.99.
Por consiguiente, se considera que el Modelo Modificado amplía el rango de aplicabilidad (distintas arcillas) y mejora la capacidad de estimación (propiedades dinámicas) del Modelo tipo Masing.
Las figuras 10 y 11 presentan una comparación de las curvas G-γ y λ-γ con resultados experimentales obtenidos en arcillas marinas y arcillas lacustres. En estas figuras se aprecia con mayor claridad el alto grado de predicción del modelo propuesto. Además, se puede verificar que a mayor índice de plasticidad, mayores serán los valores de las deformaciones de referencia empleados en la modelación, γrG y γrλ .


Los valores de los coeficientes de correlación obtenidos en la modelación son bastante buenos; por lo que se puede argüir que el Modelo Modificado es aplicable a distintas arcillas. Sin embargo, durante la modelación se percibió que a mayor índice de plasticidad, la variabilidad en los coeficientes de correlación aumenta. Esto puede deberse a características mineralógicas, fisicoquímicas y ambiente de depositación del material.
Conclusiones
A partir de un análisis paramétrico del Modelo tipo Masing y de resultados experimentales, se planteó un Modelo Modificado que permite obtener mejores estimaciones de las propiedades dinámicas de distintas arcillas.
Se demostró que el parámetro A definido en el Modelo tipo Masing corresponde a una constante igual a uno y por lo tanto, es independiente del índice de plasticidad del material a modelar.
Se probó que la deformación de referencia necesaria para obtener la relación teórica G-γ , difiere de la deformación requerida para obtener la relación λ-γ . Adicionalmente, se demostró que estas deformaciones, γrG y γrλ , corresponden a los puntos de inflexión de las curvas G-γ y λ-γ y a su vez, son independientes del parámetro B.
Los parámetros BG y Bλ definen la geometría particular de las relaciones G-γ y λ-γ , respectivamente. Para el caso de las arcillas, estos parámetros son funciones del índice de plasticidad y se pueden obtener empleando correlaciones (e.g. figura 7) o procedimientos matemáticos alternos (e.g. mínimos cuadrados). Esta versatilidad en el cálculo de los parámetros BG y Bλ , permite que el Modelo Modificado pueda ser aplicado a cualquier tipo de material.
Actualmente, el Modelo Modificado tipo Masing está formulado para estimar propiedades dinámicas exclusivamente de arcillas normalmente consolidadas, donde los parámetros B y γr son funciones del índice de plasticidad. Sin embargo, este Modelo Modificado brinda una plataforma de partida a investigaciones futuras, dedicadas al estudio de las propiedades dinámicas de materiales con comportamiento elasto-plástico, donde los parámetros B y γr no dependan necesariamente del IP (e.g. suelos granulares y polímeros).
Agradecimientos
Los autores agradecen al Dr. Osvaldo Flores por proporcionar los datos experimentales presentados en el Anexo, así como al Instituto de Ingeniería de la UNAM y al Consejo Nacional de Ciencia y Tecnología CONACyT por el apoyo económico otorgado al primer autor. Igualmente, se agradece al Posgrado de Ingeniería de la UNAM por la formación académica brindada al primer autor.
Referencias
Anderson, D G y Jr. F E Richart (1976), "Effects of straining on shear modulus of clays", ASCE Journal of the Geotechnical Engineering Division, Vol. 102, No. GT9, pp. 975-987. [ Links ]
Hildebrand, D K y R. L. Ott (1996), Estadística aplicada a la administración y a la economía, Pearson Prentice Hall, Addison Wesley Iberoamericana S.A., México, Primera reimpresión. [ Links ]
Flores, O, M P Romo, L Vega, B García y R Flores (1999), "Ensayes estáticos y dinámicos de las arcillas del corazón impermeable de la presa revolución mexicana (El Guineo)", Informe Interno del Instituto de Ingeniería, UNAM, México. [ Links ]
González, C M, O Flores, M P Romo y C Dorado (2007), "Modelación de las propiedades dinámicas de suelos compactados saturados", XIII Conferencia Panamericana de Mecánica de Suelos e Ingeniería Geotécnica, Isla Margarita, Venezuela. [ Links ]
Hardin, B O y V P Drnevich (1972), "Shear modulus and damping in soils: design equations and curves", ASCE Journal of the Soil Mechanics and Foundation Division, Vol. 98, No. SM7, pp. 667-692. [ Links ]
Ishihara, K (1996), Soil behavior in earthquake geotechnics, Clarendon Press, Oxford University Press, Great Britain. [ Links ]
Ossa, A y M P Romo (2008), "A model for EPS dynamic shear modulus and damping ratio", The First Panamerican Geosynthetics Conference, Cancún, México. [ Links ]
Romo, M P (1990), "Comportamiento dinámico de la arcilla de la Ciudad de México y su repercusión en la ingeniería de cimentaciones", Simposio El Subsuelo de la Cuenca del Valle de México y su Relación con la Ingeniería de Cimentaciones a Cinco Años del Sismo, pp. 83-94. [ Links ]
Romo, M P (1995), "Clay behavior, ground response and soil-structure interaction studies in México city (state of the art paper)", Third International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis Missouri (USA), Vol. II, pp. 1039-1051. [ Links ]
Seed, H B e I M Idriss (1970), "Soil moduli and damping factors for dynamics response analysis", Report Earthquake Engineering Research Centre, University of California, Berkeley, USA. [ Links ]














