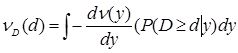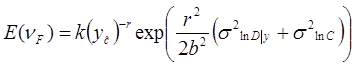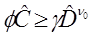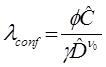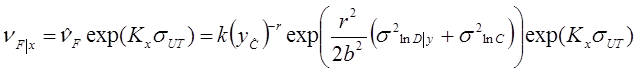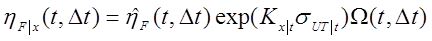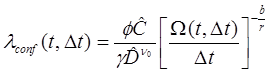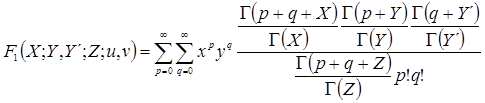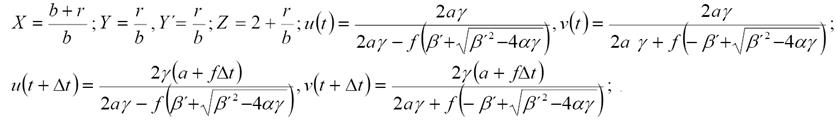INTRODUCCIÓN
La seguridad de un sistema estructural se provee especificando capacidades a los elementos estructurales que implícitamente cumplen con un nivel de confiabilidad aceptable; sin embargo, el sistema estructural continuamente está expuesto a condiciones de carga de eventos naturales (ej. sismo, viento, oleaje, inundación, etc.). Al término de estos eventos, el sistema estructural sufre cierto deterioro en sus propiedades mecánicas dando lugar a que se debilite su capacidad estructural y al mismo tiempo se incremente su demanda estructural ante cierto nivel de solicitación. Como resultado de lo anterior, el valor de la confiabilidad del sistema estructural se reduce a medida que pasa el tiempo, llegando hasta el punto en el que dicho sistema presente niveles de confiabilidad no deseados. Lo anterior hace ver la necesidad de desarrollar criterios que permitan evaluar la confiabilidad estructural en el tiempo con el fin de conocer qué tan segura está la estructura a lo largo de su vida útil.
Dada la importancia de evaluar el estado de las estructuras que sufren deterioro, varios autores han propuesto diversos criterios para evaluar dicho estado en término de niveles de confiabilidad, por ejemplo: a) mediante procesos de Markov (Montes et al., 2003; Straub, 2009); b) simulación de Monte Carlo (Díaz y Esteva, 1997); c) simulación direccional (Melchers, 1992; Mori y Ellinwood, 1993) y d) aproximaciones basadas en métodos FORM/SORM (Rackwitz, 2001). Por otro lado, Frangopol et al., (2004) hacen una revisión general sobre modelos probabilistas para evaluar el ciclo de vida de estructuras que presentan deterioro estructural; sin embargo, ninguno de estos enfoques evalúa la confiabilidad en términos del factor de confianza al término de un intervalo de tiempo.
El factor de confianza,
En este trabajo se propone un criterio para evaluar la confiabilidad en términos del factor de confianza,
FACTOR DE CONFIANZA SIN CONSIDERAR EL DETERIORO ESTRUCTURAL
Una manera de calcular la tasa media anual de falla es separando las incertidumbres que involucran a la demanda sísmica de la capacidad estructural como sigue (Cornell, 1968; Esteva, 1968; Cornell et al., 2002):
donde
Las ecuaciones 1 y 2 pueden ser resueltas por medio de integración numérica o por medio de métodos simplificados. Con la finalidad de resolver las expresiones antes mencionadas se han propuesto las siguientes consideraciones utilizando un enfoque simplificado como sigue (Kennedy y Short, 1994; Cornell et al., 2002):
a) La curva de peligro, v(y) se representa para la intensidad de interés mediante la función
b) La mediana de la demanda estructural,
c) La capacidad estructural del estado límite de interés presenta una mediana de la capacidad,
A partir de las consideraciones a, b y c, la ecuación 1 se transforma como sigue (Kennedy y Short, 1994):
Considerando las simplificaciones a y c, la tasa media anual de falla,
Introduciendo las incertidumbres epistémicas, el valor esperado de la tasa media anual de falla obtenida por Cornell et al. (2002) es igual a:
donde
donde
A partir de la formulación anterior, se deduce el factor de confianza,
El nivel de confianza para que se presente el factor de confianza se expresa como sigue:
donde
Donde
FACTOR DE CONFIANZA EN FUNCIÓN DEL TIEMPO
En lo que sigue se extiende la metodología presentada en la sección anterior para el caso en el que las propiedades mecánicas de los elementos estructurales cambian en el tiempo, y como consecuencia decrece el valor de la capacidad estructural y aumenta la demanda estructural ante una secuencia de solicitaciones que se presente en cierto intervalo de tiempo.
La tasa media anual de falla,
donde:
donde
En el formato Demand and Capacity Factor Design (DCFD, Cornell et al., 2002) se asume que la tasa anual de falla,
Resolviendo y separando términos con respecto a la ecuación anterior, se llega a la siguiente expresión del factor de confianza ,
CASO EN EL QUE SE CONSIDERA QUE LA CAPACIDAD (NO-LINEAL) Y LA DEMANDA ESTRUCTURAL VARÍAN SIMULTÁNEAMENTE EN EL TIEMPO
La confiabilidad estructural expresada en términos del número esperado de fallas al final del intervalo de tiempo
donde
Con la finalidad de considerar de manera simultánea la capacidad estructural (no-lineal) y la demanda estructural, se hacen las siguientes hipótesis:
d) La varianza del logaritmo natural tanto de la capacidad,
e) Los parámetros
f) La mediana de la capacidad estructural varía en el tiempo como una función polinomial de segundo grado, dada por:
g) La mediana de la demanda estructural,
Tomando en cuenta las consideraciones a, c, d, e, f y g e integrando la ecuación 16, se obtiene la siguiente expresión cerrada para estimar el número esperado de fallas al término del intervalo de tiempo
donde:
donde
donde:
Siguiendo las mismas suposiciones para llegar a la ecuación 13, se tiene:
De la ecuación 22 es posible obtener el factor de confianza que considera la variación de la capacidad no-lineal (función de segundo orden) y la demanda estructural de manera simultánea, para el intervalo de tiempo de interés, como sigue:
CASO EN EL QUE SE CONSIDERA QUE LA CAPACIDAD (LINEAL) Y LA DEMANDA ESTRUCTURAL VARÍAN SIMULTÁNEAMENTE EN EL TIEMPO
Con la finalidad de conocer la variación tanto de la capacidad estructural (lineal) como de la demanda sísmica, dada una intensidad, en el intervalo de tiempo
h) La mediana de la capacidad,
Considerando las suposiciones a, c, d, e, f y h e integrando la ecuación 16, el número esperado fallas que considera la variación de manera simultánea la capacidad (lineal) y de la demanda estructural al final del intervalo de interés, es igual a:
donde:
Donde
donde
Siguiendo un procedimiento similar para llegar a la ecuación 23, el factor de confianza que considera la variación tanto de la capacidad estructural como de la demanda sísmica, al término del intervalo de tiempo
donde
CASO EN EL QUE SE CONSIDERA QUE LA CAPACIDAD (LINEAL) VARÍA EN EL TIEMPO, MIENTRAS QUE LA DEMANDA ESTRUCTURAL ES INDEPENDIENTE DEL TIEMPO
Con la finalidad de considerar la variación en el tiempo de la capacidad estructural y suponiendo que la demanda estructural es constante, Torres y Ruiz (2007) resolvieron la ecuación 16 considerando las suposiciones a, b, c, d, e, y h. El resultado es el siguiente:
donde:
donde
Con la ecuación anterior se evalúa el factor de confianza al término del intervalo de interés cuando sólo se considera el deterioro estructural de la capacidad, suponiendo que la demanda estructural no varía en el tiempo.
EJEMPLO
Se obtiene el factor de confianza,
SIMULACIÓN DE ACELEROGRAMAS
La carga extraordinaria que históricamente ha producido daños considerables y casos de colapso en la zona geográfica en la que se ubica el sistema estructural en estudio, son los movimientos sísmicos. Dada la escasa información de registros sísmicos en el sitio en estudio es necesario generar movimientos sísmicos sintéticos. Para la simulación de los acelerogramas sintéticos se consideró que el movimiento sísmico que se simula sigue un proceso estocástico ergódico Gaussiano no-estacionario. Se simularon 100 acelerogramas sintéticos a partir de los registro obtenidos en la estación de la Secretaría de Comunicaciones y Transportes (SCT) el 19 de septiembre de 1985 (Grigoriu et al.,1988).
SIMULACIÓN DE INTENSIDADES Y TIEMPOS DE ESPERA
Con la finalidad de evaluar la evolución del daño estructural ante secuencias sísmicas es necesario simular tanto la ocurrencia de eventos sísmicos como su intensidad. Con base en lo anterior, se simularon intensidades a partir de la curva de peligro sísmico asociado al periodo fundamental de la estructura. La curva de peligro sísmico corresponde al sitio de SCT con un porcentaje de amortiguamiento crítico igual a 5 %.
La ocurrencia de los eventos sísmicos se supuso como un proceso estocástico de Poisson, por lo que sus tiempos de espera presentan una distribución de probabilidades de tipo exponencial. Para la simulación de los tiempos de espera se supuso que el número medio de tiempos de espera entre eventos sísmicos intensos es igual a 5 años.
Se construyeron 20 historias de eventos simulados a partir de la simulación de intensidades y tiempos de espera considerando un intervalo de tiempo de 150 años. En este estudio sólo se seleccionaron intensidades mayores a 100 cm/seg2 ya que se observó que intensidades menores producían daño despreciable. Con base en lo anterior, se presentaron 8, 11 y 15 intensidades mayores a 100 cm/seg2 al término de 50, 100, y 150 años. En la figura 3 se muestra un ejemplo de historia de eventos simulados, se hace notar que se presentan 4 intensidades mayores a 100 cm/seg2, mismas que representan 0, 2 y 4 secuencias sísmicas al termino de 50, 100 y 150 años, respectivamente.
CAPACIDAD ESTRUCTURAL EN EL TIEMPO
Con la finalidad de evaluar la evolución de la capacidad estructural a causa del daño acumulado por secuencias sísmicas, al término de un intervalo de tiempo, se sometió a la estructura a una serie de análisis dinámicos no lineales "paso a paso". Con base en las 20 historias de eventos simulados (descritas en la sección anterior), se asoció aleatoriamente un aceleragrama sintético a cada intensidad mayor a 100 cm/seg2. El acelerograma seleccionado se escaló de manera que la intensidad simulada correspondiera a la intensidad que presenta su espectro de pseudoaceleracion para T=1.03 seg (periodo fundamental de la estructura). Posterior a las secuencias sísmicas, se aplicó una aceleración monotónicamente creciente simulando la acción de un análisis estático no-lineal. En los casos de historias de eventos simulados en donde no se presentaron intensidades mayores a 100 cm/seg2, sólo se aplicó una aceleración monotónicamente creciente. Los análisis dinámicos no lineales se llevaron a cabo en el programa Drain 2D (Campos y Esteva, 1997) donde se incorpora un modelo histérico que considera la degradación de rigidez y resistencia. Se consideró que la falla en la estructura se presenta en el instante cuando se articulan todas las vigas y columnas de un entrepiso. En el caso del edificio en estudio, el tercer entrepiso resultó ser el crítico. En las figura 4 a, figura 4 b y figura 4 c se muestran las curvas de capacidad (CC) con daño acumulado para los intervalos de 50, 100 y 150 años después de construida la estructura.
En la figura 4 se hace notar la disminución de rigidez y resistencia en las curvas de capacidad a medida que se incrementa el intervalo de tiempo de análisis y con esto, una mayor probabilidad de que se presente un intensidad mayor o igual al umbral de intensidad (100 cm/seg2) que produce daño a la estructura. La figura 4a muestra 8 curvas de capacidad, CC, dado que sólo ocurren 8 intensidades mayores a 100 cm/seg2, para el caso de 100 y 150 años (figura 4 b y c) se presentan 11 y 15 curvas de capacidad.
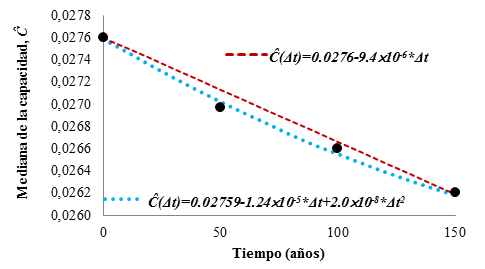
La figura 5 muestra los valores de la mediana de la capacidad al término de los intervalos de tiempo en estudio (0, 50, 100 y 150 años) considerando que dichos valores siguen una distribución de tipo lognormal. En este estudio se caracteriza la degradación de la capacidad estructural en el tiempo como un polinomio de segundo grado (no-lineal) y alternativamente, como una función lineal. En la figura 5 se muestran los valores de ajuste de ambos criterios no-lineal (ecuación 17) y lineal (ecuación 24) a lo largo del intervalo de tiempo en estudio. Los valores de la desviación estándar del logaritmo natural de la capacidad,
DEMANDA ESTRUCTURAL SÍSMICA EN EL TIEMPO
La demanda sísmica al término de distintos intervalos de tiempo se obtuvo mediante análisis dinámicos no lineales "paso a paso". Para su obtención, se utilizaron las mismas historias de eventos simulados que se emplearon para obtener la capacidad estructural en el tiempo, sólo que al final de cada intervalo en estudio, se cambió la carga monotónicamente creciente por un acelerograma sintético elegido aleatoriamente, y este se fue escalando hasta que la estructura presentó la falla incipiente. En la figura 6 se muestran los valores de la mediana de la demanda sísmica al término de 0, 50, 100 y 150 años. Con base en los resultados, se verificó que dichos valores obedecieran a una distribución de tipo lognormal. La figura 6 muestra que se presentan valores de daño inicial acumulado al término de 50, 100 y 150 años y este se incrementa a medida que aumenta el intervalo de tiempo. Dicho daño se debe al efecto de las secuencias sísmicas.
Las figuras 7 a, b, c y d muestran los ajustes de los valores de la mediana de la demanda al término de 0, 50, 100 y 150 años, respectivamente. Se utilizó la ecuación 18 para llevar a cabo el ajuste de dichos valores. Con base en la ecuación 18, los parámetros a, f y b definen la forma de los valores de la mediana de la demanda, dada una intensidad, mientras que el parámetro g define el valor del daño inicial acumulado. Dada la similitud en tendencia con los valores de la mediana de la demanda, los valores de las desviaciones estándar del logaritmo natural de la demanda,
FACTOR DE CORRECCIÓN EN EL TIEMPO
Para evaluar el factor de corrección en el tiempo es necesario conocer el valor de los parámetros de las ecuaciones 20, 26 y 30. Los parámetros α, β y γ se presentan en la figura 5, los valores que ajustan la forma de la mediana de la demanda a, f y b se muestran en la figura 7, y los parámetros que ajustan la forma de la curva de peligro sísmico para la intensidad de interés, tienen un valor igual a k=1.7(10-4 y r= 3.75. A juicio de los autores, se consideró un valor de 0.2 en las varianzas epistémicas,
La figura 8 muestra diferencias del 22.6 %, 20.1 %, 24 % y del 9.4 %, 6.7 %, 11.3 % al término de 50, 100 y 150 años cuando no se considera la variación de la demanda sísmica en el tiempo (Torres y Ruiz, 2007) comparado con los criterios que sí consideran dicha variación (Tolentino et al., 2012) y este estudio. Las diferencias entre los criterios que consideran tanto la variación de la capacidad como la demanda, al término de un intervalo de tiempo (ecuaciones 22 y 28), resultaron del orden de 17.1, 16.7 y 18.2 al término de 50, 100 y 150 años.
EVALUACIÓN DE LA CONFIABILIDAD ESTRUCTURAL EN EL TIEMPO
El factor de confianza,
En la figura 10 se muestran el nivel de confianza al término de diferentes instantes de tiempo considerando los casos: a) sin daño (Cornell et al., 2002), b) Sólo varía la capacidad estructural (lineal) en el tiempo (Torres y Ruiz, 2007), c) varía tanto la capacidad (lineal) como la demanda en el tiempo, y d) varía la capacidad (no-lineal) y la demanda en el tiempo. La figura 10 muestra un disminución del grado de confianza del 87.7 %, 83.7 % y 78.5% para el criterio que sólo considera la variación de la capacidad en el tiempo, dicha pequeña disminución es como se esperaba dado que no se considera la incertidumbre que introduce el considerar la variación de la demanda sísmica en el tiempo. Con respecto a los casos que sí consideran la demanda sísmica, se tiene un disminución del 79.3 %, 60.8 % y 36.7% para el caso que considera la variación (lineal) de la capacidad y la demanda en el tiempo, y del 84.8 %, 68.3 % y 45.2% para el caso desarrollado en este estudio.
CONCLUSIONES
Se propone un criterio para evaluar el factor de confianza y su correspondiente nivel de confianza que considera la variación de la demanda sísmica y la capacidad (mediante una función tipo polinomio de segundo grado), al término de un intervalo de tiempo. La formulación que se propone utiliza expresiones matemáticas cerradas, con formato similar a las expresiones descritas en los códigos de diseño. Dicho factor se evalúa para un edificio de concreto reforzado sujeto a secuencias sísmicas para los siguientes casos: a) no se considera el daño en el tiempo, b) sólo se considera que varía la capacidad (lineal) en el tiempo, c) se considera que la capacidad (lineal) y la demanda varían simultáneamente en el tiempo, y d) varían tanto la capacidad (no-lineal) como la demanda en el tiempo.
Se observó que el modelo de degradación no-lineal de la capacidad estructural se apega al comportamiento del edificio comparado con el modelo de degradación lineal de la capacidad estructural. Las diferencias de porcentajes entre estos criterios son del orden de 3.5 %, 5.5 % y 6 % al término de 50, 100 y 150 años. Se puede decir que estos porcentajes representan una diferencia pequeña en términos de ingeniería estructural; sin embargo, para que se presente el mismo valor de factor de confianza en ambos criterios, tuvieron que transcurrir 20 años; por ejemplo,
Las expresiones propuestas pueden aplicarse a cualquier tipo de sistema estructural (ej. edificios, torres de transmisión, puentes, plataforma marinas, plantas nucleares, tanques de almacenamiento, etc.), sometido a una o múltiples cargas ambientales (ej. sismo, viento, oleaje, etc.), y pueden considerar diferentes estados límite. El criterio propuesto se puede extender para establecer criterios de diseño para un nivel confiabilidad pre-escrito (ej. normas de diseño para plataformas marinas fijas), por otro lado, se pueden establecer planes de mantenimiento para la búsqueda de intervalos de tiempo óptimo de inspección y mantenimiento.











 nueva página del texto (beta)
nueva página del texto (beta)