Introducción
Los tanques de almacenamiento de líquido por lo general son clasificados por los códigos de diseño como estructuras del grupo A, ya que deben de permanecer funcionando antes, durante y después de la ocurrencia de un sismo. Lo mismo es aplicable para tanques que almacenan agua potable, de los cuales depende una comunidad, que para tanques industriales que almacenan sustancias tóxicas o peligrosas y que en caso de una falla estructural producirían daño ecológico y pérdidas de vidas humanas.
Los tanques elevados para almacenar líquidos están formados por el contenedor, que se ubica en su parte superior, y la plataforma estructural que funciona de apoyo. Actualmente en México se ha construido una gran cantidad de tanques elevados con formas estructurales tipo péndulo invertido, con formas estructurales que cumplen más con el aspecto arquitectónico que con el estructural (figura 1).
Se considera que una estructura se comporta como péndulo invertido cuando más del 50% de su masa está ubicada en su parte superior, además de que está apoyada en una columna, tal que la formación de una articulación plástica en ella generará el colapso. El momento másico de inercia de la masa produce rotación de la misma alrededor del eje vertical de la columna, lo que induce un grado de libertad adicional. La importancia de los efectos másicos inerciales depende de la relación: radio de giro de la masa con respecto a la rigidez a la rotación de la columna en su parte superior.
Existe una gran cantidad de referencias bibliográficas en las que se estudia el comportamiento y diseño sísmico de tanques apoyados sobre el terreno, pero son escasas las que hacen referencia a tanques elevados (Hernández et al., 2017). En el análisis sísmico de contenedores elevados intervienen dos aspectos: (1) durante una excitación sísmica, el líquido contenido en el tanque ejerce fuerzas hidrodinámicas sobre las paredes y en su base, y (2) el elemento estructural en que se apoya es por lo general menos dúctil y con poca redundancia comparada con la de un edificio.
Los tanques elevados apoyados en una plataforma formada por multicolumnas presentan un tipo de falla originada principalmente por torsión del contenedor (Ramiah et al., 1966; Sajjad y Jain, 1994; Durgesh, 2003; Dutta et al., 2000; Jaiswal et al., 2007). Sin embargo, los tanques elevados que más fallas estructurales han presentado durante un evento sísmico, son los que se encuentran apoyados en una columna que funciona como elemento resistente (Durgesh, 2003; Jain et al., 2002a y 2002b; El Damatty et al., 1997). La falla característica en este tipo de contenedor se debe más a un comportamiento de un péndulo invertido, en donde el momento másico del contenedor produce un grado de libertad adicional, produciendo que su base rote alrededor de su eje vertical. Este mismo comportamiento se presenta en tanques que aparentemente están apoyados sobre el terreno (Sezen et al., 2008), pero que en realidad están apoyados en una serie de pilas-columnas que permiten traslación y rotación de la base del contenedor (figura 2).
Hipótesis de cálculo
Para desarrollar las ecuaciones de movimiento del modelo que representa un tanque elevado considerando el efecto de la rotación en la base del contenedor con forma arbitraria, se realizarán las siguientes hipótesis:
El fluido tiene superficie libre, tal que al moverse genera oleaje con una altura pequeña, así la ecuación de movimiento del líquido puede linealizarse, además se supone que el líquido es no viscoso, irrotacional e incompresible, con lo cual se válida la aplicación de la teoría del potencial. Como en la teoría del potencial no es posible tomar en cuenta la disipación de energía, el amortiguamiento del líquido se considera en la ecuación de movimiento por analogía de un oscilador amortiguado.
Las paredes del contenedor se consideran indeformables ante los efectos dinámicos del fluido. Lo anterior simplifica el problema de interacción fluido-estructura. Si se desea considerar de manera más detallada tal efecto, será necesario modelar el fluido por medio de algún programa de cómputo que consideré elementos fluido y elementos estructurales. Un análisis de las técnicas numéricas aplicables en este tipo de problemas como son los métodos de Elemento Finito, Elementos de Frontera, Diferencias Finitas, Volumen Finito y Marcadores y Celdas, se pueden consultar en Hernández (2004).
El material que forma la plataforma de apoyo del contenedor se considera en el intervalo elástico.
Se desprecian los efectos de la interacción suelo-estructura.
Analogía de masas concentradas
El modelo masa-resorte-amortiguador es una simplificación de un problema complejo de interacción fluido-estructura-suelo y trata de complementar el modelo simplificado sugerido para el análisis sísmico de este tipo de estructuras en México.
El sistema de ecuaciones en la frontera que gobiernan el comportamiento dinámico de un líquido contenido en un recipiente es no lineal debido principalmente a la ecuación cinemática de la superficie del fluido. Dicha ecuación contiene términos de orden superior lo que da lugar a un sistema de ecuaciones no lineales que representan el dominio del líquido (Hernández, Heredia y Aldama, 2007). Si la ecuación cinemática se linealiza es posible resolver el sistema de ecuaciones de frontera por medio de la teoría del potencial. Graham y Rodríguez en 1952 fueron los primeros en considerar la teoría del potencial para resolver el problema dinámico de tanques de aeronaves (Abramson, 1966). Estos autores supusieron que las presiones dinámicas del líquido sobre las paredes del contenedor pueden separarse en dos: una convectiva y otra impulsiva. Las presiones impulsivas están asociadas con las fuerzas de inercia producidas por movimientos impulsivos de las paredes del tanque y son directamente proporcionales a las aceraciones del mismo. Las presiones convectivas se producen por la oscilación del fluido en la superficie libre y son consecuencia de las presiones impulsivas. Retomando el enfoque de los autores anteriores, Housner (1957) propuso un procedimiento de análisis basado en un modelo masa-resorte que posteriormente fue modificado por Veletsos y Yang (1977).
En las obras civiles las paredes de los contenedores pueden ser de concreto reforzado o de mampostería, en cuyo caso se consideran como tanques con paredes rígidas; sí las paredes del contenedor son de acero estructural se pueden considerar como tanques con paredes flexibles. Wozniak y Michell (1978) establecieron que los efectos hidrodinámicos impulsivos en tanques con paredes rígidas son similares a los que presentarían los tanques con paredes flexibles por lo que la diferencia en su comportamiento puede ser despreciable. Resultados experimentales en tanques de almacenamiento con superficie libre muestran claramente que existe un comportamiento amortiguado en la respuesta del líquido asociado a la disipación de energía durante el movimiento del líquido (Case y Parkinson, 1957). En la teoría del potencial no es posible tomar en cuenta la disipación de energía por lo que en los trabajos en los que se considera el amortiguamiento, éste se introduce en la ecuación de movimiento por la analogía de un oscilador amortiguado. Faltinsen (1974) sugiere un valor de amortiguamiento con respecto al crítico del orden de 0.3 a 0.5 por ciento para líquidos.
Los códigos de diseño (MDOC-2015, NTC-2004, API-STD-650-2013, AWWA D100-2000, Eurocódigo-8) sugieren el uso de modelos simplificados masas-resortes para modelar el fluido. En México las ecuaciones propuestas en la Normas Técnicas Complementarias para el diseño y ejecución de obras e instalaciones hidráulicas (NTC-2004), así como en el Manual de Diseño de Obras Civiles (MDOC-2015) tienen su origen en el modelo simplificado sugerido por Housner (1957) para contenedores con paredes rígidas y proponen considerar una masa para modelar el efecto impulsivo y otra para el modo convectivo. Implícitamente las ecuaciones propuestas consideran que el contenedor no presenta cabeceo, es decir, no existe un momento debido a la rotación del contenedor sobre su base.
Las expresiones en función de masas-resortes que representan el comportamiento dinámico de tanques cilíndricos apoyados sobre el terreno se pueden encontrar en Haroun (1980); para tanques esféricos de aeronaves en Tung (1989); para tanques cilíndricos y rectangulares de aeronaves en Graham y Rodriguez (1952) y en Roberts et al. (1965); y para tanques con forma cónica en Saafan (2004)).
En la figura 3 se muestra un diagrama esquemático del modelo equivalente masa-resorte que representa el líquido dentro de un contenedor con paredes rígidas. Consiste de una masa rígida que se mueve igual que las paredes del tanque, m f , y una serie de masas, m n que representan las “n” masas equivalentes del oleaje o modos convectivos. Cada masa modal, m n está restringida por un resorte con rigidez, k n y un amortiguador, C n . Las distancias que ubican a cada una de las masas equivalentes se pueden referir con respecto al centro de masas del líquido, como h f , h 1 y h n ; o con respecto al fondo del contenedor como H f , H 1 y H n . La masa m f que se mueve junto con las paredes tiene un momento másico de inercia equivalente I f .
En el modelo la masa total del fluido es,
el momento de inercia másico equivalente del líquido como si estuviera solidificado, alrededor del eje z y que pasa por su centro de masas es,
el centro de masas debe conservarse, por lo que:
La constante del resorte, k n , se puede determinar de la definición de las frecuencias de vibrar de cada modo convectivo como,
El contenedor sin líquido y con altura total H t, puede modelarse considerando que su masa se encuentra concentrada en su centro de masas, m t, y tienen un momento másico de inercia, I t, medido con respecto a su centro de masas (figura 3).
De estudios realizados en estructuras en voladizo modeladas con masas concentradas y por medio de métodos energéticos (Wilson, 2003) se recomienda, con el fin de considerar adecuadamente la masa del elemento estructural que participa en un análisis dinámico, usar un coeficiente de 0.375 que corresponde a la proporción de la masa de los elementos estructurales alrededor de un nodo. De esta forma la masa efectiva que se ubica en el nodo imaginario en la parte superior de la columna está formada por:
donde m f representa la masa impulsiva del líquido, m t es la masa del contenedor vacío y m p es la masa del elemento lateral resistente.
Ecuación general de movimiento
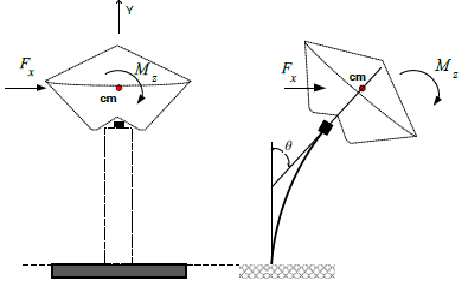
En la figura 4 se muestra un contenedor elevado apoyado en un elemento estructural representado por una columna con altura L, el centro de masas del sistema contenedor-líquido se encuentra ubicado a una distancia y c medida desde la parte inferior del contenedor. En la deducción de las ecuaciones se considera que el sistema se comporta como un oscilador con dos grados de libertad acoplados: traslación horizontal y cabeceo.
Sea q n (t) el desplazamiento relFativo de las masas equivalentes que representan el efecto convectivo del líquido con respecto a las paredes del contenedor; U(t) el desplazamiento absoluto de las paredes del contenedor en la dirección horizontal y θ es el ángulo de rotación. La ecuación de Lagrange del sistema es,
donde X i representa el vector de coordenadas generalizadas,
El Lagrangiano, que aparece en la ecuación 6, por definición es: L= T - U p, donde la energía cinética es,
y la energía potencial,
Las ecuaciones 9 y 10 referidas al fondo del contenedor se pueden escribir como,
y
donde las distancias H f y H n están referidas en la figura 3. Sustituyendo las ecuaciones 11 y 12 en el Lagrangiano se tiene,
La energía disipada se puede representar como (Ibrahim, 2005):
en donde ξ n es el porcentaje de amortiguamiento con respecto al crítico.
Equilibrio de fuerzas horizontales
Sustituyendo en la ecuación de Lagrange, el Lagrangiano dado por la ecuación 13 y considerando X i = U (t), se tiene
Realizando las derivadas correspondientes, la ecuación de equilibrio dinámico de fuerzas horizontales se puede escribir como,
La aceleración absoluta del sistema (figura 4) es,
donde Ü
g
(t) representa la aceleración del terreno en la dirección horizontal y
Equilibrio de las masas que producen oleaje
Si se considera en la ecuación de Lagrange, X i = q n , se tiene
Realizando las derivadas correspondientes y considerando la relación 17, la ecuación que representa el comportamiento del líquido dentro del contenedor es,
Ecuaciones para momento de volteo
Si se considera en la ecuación de Lagrange, Xi = θ, se tiene
Realizando las derivadas correspondientes se tiene la ecuación de equilibrio dinámico para el momento de volteo,
donde el momento de inercia del contenedor-liquido referido a la base del mismo es,
Ecuaciones de equilibrio de la estructura
Se considerará que en la base del contenedor existe un elemento axialmente rígido, tal y como en la práctica sucede en tanques con plataforma de acero al colocarse el anillo base y en plataformas de concreto al colocarse las trabes que forman el sistema de fondo del contenedor (figura 5). Una fuerza aplicada en la base del contenedor en la dirección horizontal, F x, y un momento alrededor del eje z, M z , están relacionados con los grados de libertad en la base del contenedor con la matriz de rigidez (McGuire et al., 2000) del elemento lateral resistente, considerándolo como empotrado en su base con:
donde K xx y K θθ son la rigidez lateral por flexión y por rotación del elemento estructural de apoyo, respectivamente. La rigidez a rotación debido a la traslación es K x θ = K θx.
Las ecuaciones 18 y 22 se pueden escribir como:
Las ecuaciones 25 y 26 junto con la ecuación 20, se pueden expandir en la sumatoria para “n” masas equivalentes que representan el efecto convectivo del líquido. Así, en forma matricial para el caso en el que se considere n=3 masas convectivas,
Si el contenedor está apoyado en un elemento lateral de sección transversal constante los términos que forman la matriz de rigidez, despreciando las deformaciones por cortante son:
donde E c es el módulo de elasticidad del material que forma la columna, I c , es el momento de inercia de la sección transversal de la columna en la dirección de análisis y L es la altura de la misma. La ecuación de movimiento 27 se puede escribir como:
donde,
La ecuación 29 puede resolverse paso a paso por cualquier método convencional o por medio de un análisis modal.
Como puede observarse en la ecuación 27 la magnitud del momento producido en el fondo del contenedor depende de la rigidez a la rotación del elemento de apoyo y de la magnitud del momento másico de inercia del contenedor-líquido. Por lo que sí dicho elemento de apoyo es lo suficientemente rígido a la rotación y el momento másico de inercia del contenedor-líquido es pequeño, entonces se tiene un sistema de un grado de libertad en traslación. Pero si el sistema de apoyo es un monopolo y además el momento másico del recipiente-líquido no puede despreciarse, entonces el valor de la rotación contenedor debe ser considerado en la respuesta estructural.
Modelos considerados
Se considerarán los cuatro modelos simplificados mostrados en la figura 6, que varían según sea el número de masas equivalentes del líquido que representan los modos convectivos y las propiedades de rigidez del elemento de apoyo. En este trabajo se considera que el contenedor puede desplazarse horizontalmente y rotar con respecto a su base, de tal manera que se llaman modelo M1 a aquel que tiene una masa para el modo impulsivo y tres masas para los modos convectivos; y como modelo M2 a aquel que tiene una masa para representar cada modo.
Si el contenedor únicamente se puede desplazar en traslación, se considera como modelo M3 a aquel que tiene tres masas para representar los modos convectivos y una para el impulsivo; y como modelo M4 a aquel recomendado en la mayoría de los códigos de diseño (MDOC-2015, NTC-2004) con una masa que representa el modo convectivo, una para del modo impulsivo.
En la práctica profesional los tanques elevados son calculados utilizando algún programa de cómputo. Los programas usados con mayor frecuencia están limitados, dado que no permiten modelar la interacción del fluido con la estructura y los que sí son capaces de resolver este problema tienen menos difusión, son poco utilizados por su relativo alto costo y demandan un mayor conocimiento teórico del usuario. Por lo tanto, dicha interacción se desprecia y se supone que se obtienen resultados confiables al colocar una masa concentrada fija a las paredes del mismo, en un nodo ubicado en el centro de gravedad del recipiente con masa equivalente a la masa total del líquido más la del contenedor; el recipiente normalmente se diseña por carga hidrostática. Mediante este criterio se desprecia la altura de ola que puede generar derrames del líquido debido al movimiento sísmico o daño en las paredes del contenedor.
Los tanques elevados de almacenamiento apoyados sobre un elemento resistente o sobre una hilera de columnas perpendicular a la dirección de análisis, cumplen con la definición de péndulo invertido. Para este tipo de estructuras según el MDOC-2015 y la NTC-2017 se puede hacer un análisis dinámico por medio del método estático en el que se considere la fuerza lateral calculada con,
donde c es el coeficiente sísmico seleccionado según la zona sísmica, m total , es la masa del sistema que se considera como la masa del líquido más la masa del tanque. El término F a = QR, donde Q y R son el factor de comportamiento sísmico y el factor de reducción por sobrerresistencia, respectivamente. Además de la fuerza lateral se debe considerar el efecto de las aceleraciones angulares de la masa superior con un momento aplicado en el extremo superior del elemento resistente,
donde r m es el radio de giro de la masa del péndulo invertido φ, es el giro del extremo superior del elemento resistente y x es su desplazamiento lateral.
La mayoría de los códigos de diseño sísmico permiten realizar un análisis modal para tanques elevados considerando la analogía masa-resorte-amortiguador para representar el líquido en el contenedor. Cuando se realiza este procedimiento existen divergencias en cuanto a los valores de los coeficientes de reducción Q y R que deben de usarse. Existe evidencia bibliográfica (Hernández y Rojas, 2007; Jaiswal et al., 2007) que indica que utilizar los mismos valores recomendados para edificios es erróneo. Varios códigos internacionales de diseño usan el mismo valor de F a para los modos impulsivos y convectivo. Sólo el ACI 350.3 y el Eurocódigo-8, sugieren un valor de F a = 1.0 para el modo convectivo. El tema sobre la consideración de F a diferente para el modo convectivo e impulsivo es controversial. En este trabajo, por simplicidad se usó un valor de F a = 3.6 (Jaiswal et al., 2007) para representar ambos modos. El vector de fuerzas modales se puede calcular con,
donde a(β) es la ordenada espectral que es función del valor del amortiguamiento β y del periodo del modo en cuestión; [M] es la matriz de masa inercial, {φ} es el vector modal del n-ésimo modo y C* n es el vector que contiene los factores de participación modal. El factor de importancia se consideró de I = 1.50. Las ordenadas espectrales en los códigos de diseño, están propuestas para un valor de amortiguamiento del 5%, el cual se considera adecuado para el elemento lateral resistente pero para los modos convectivos que representan el oleaje, las aceleraciones espectrales deben corregirse para un valor de amortiguamiento del 0.5%. El factor de corrección considerado en este trabajo es de 1.673 (Eurocódigo-8). Los valores de diseño se obtienen con la regla de la raíz cuadrada de la suma de los cuadrados (MDOC-2015).
Ejemplo de aplicación
Se considera un tanque elevado rectangular con paredes de concreto reforzado (figura 7) con dimensiones del contenedor de: 4.30 m de largo, 4.30 m de ancho y altura total de H = 4.0 m, con un espesor de sus paredes, fondo y techo de 0.15 m. La posición del centro de masas del contenedor sin líquido, medido a partir del fondo está a
Tabla 1. Propiedades del sistema masa-resorte-amortiguador del ejemplo
| Identificación | Frecuencia (rad/s) |
Periodo (s) |
Masa (kN s2/m) |
Rigidez (kN/m) |
Posición a partir del fondo (m) |
|---|---|---|---|---|---|
| mf | - | - | 38.85 | - | 1.46 |
| m1 | 2.76 | 2.27 | 16.37 | 125.09 | 2.38 |
| m2 | 4.81 | 1.31 | 0.6108 | 14.13 | 3.08 |
| m3 | 6.21 | 1.01 | 0.1324 | 5.09 | 3.25 |
En la tabla 1 se registran las propiedades de cada una de las masas para representar el líquido contenido en el tanque.
En la tabla 2 se muestran las frecuencias de vibrar del sistema liquido-tanque elevado y sus correspondientes periodos. En este ejemplo se integró la ecuación de movimiento considerando un porcentaje de amortiguamiento con respecto al crítico de ξ = 5% para el elemento lateral resistente (plataforma del tanque) y para el recipiente vacío (tanque); y del ξ = 0.5% para el líquido contenido en el tanque. Se usó como excitación la componente EW del registro sísmico obtenido en la estación de Central de Abasto (CA) durante el sismo del 19 de septiembre de 1985 en el Valle de México.
Tabla 2. Frecuencias y periodos de vibrar del tanque elevado del ejemplo
| Modo | Frecuencia (rad/s) | Periodo (s) | Identificación |
|---|---|---|---|
| 1 | 2.76 | 2.27 | Convectivo |
| 2 | 4.81 | 1.31 | Convectivo |
| 3 | 6.21 | 1.01 | Convectivo |
| 4 | 7.88 | 0.78 | Traslación |
| 5 | 142.42 | 0.05 | Cabeceo |
En la figura 8 se muestra la altura de ola considerando una masa para el modo convectivo (modelos M2 y M4) y considerando tres masas para representar dichos modos (modelos M1 y M3). La altura de ola máxima es de 213 cm para el caso de considerar tres masas para el modo convectivo y considerando una sola masa es de 85 cm. La influencia de la rotación de la base del contenedor tiene poca influencia en la altura de ola máxima. El resultado indica la importancia de considerar al menos tres masas para representar el modo convectivo en tanques ubicados en algunas zonas sísmicas del Valle de México.
En la figura 9 se muestra la historia de fuerza cortante obtenida con los modelos M1 y M3, en los que se consideran tres masas para el modo convectivo. Como se observa los valores obtenidos con ambos modelos es similar, obteniéndose para el modelo M1 un fuerza cortante máxima de 80.37 kN y en para el modelo M3 una fuerza de 79.34 kN. En la historia de fuerzas cortantes existen diferencias después del segundo 60 pero no influyen en el valor máximo. Para este ejemplo se puede concluir que las fuerzas producidas por las masas convectivas son pequeñas como para influir en la fuerza cortante máxima, además de que los efectos del cabeceo también tienen poca importancia en el cálculo de la fuerza cortante.
En la figura 10 se muestra la historia del momento de volteo en la cimentación del tanque, obtenida con los modelos M1 y M3. Ambos modelos consideran 3 masas para tomar en cuenta los efectos convectivos del líquido, sólo que el modelo M1 considera los efectos de rotación de la base del tanque y el M3 considera que la base del tanque no rota. Para este ejemplo, el valor máximo del momento de volteo obtenido con el modelo M1, que considera el efecto de la rotación de la base es del orden del 15% mayor que el que se obtiene con el modelo M3.
En la figura 11 se muestran los resultados de realizar un análisis modal considerando los valores de la aceleración espectral, a(β), expresadas en fracción de la gravedad que sugieren las NTC-2017, para diferentes zonas del Valle de México en función del periodo dominante del sitio y usando el modelo M1 y el modelo M5. El modelo M5 considera la masa total del tanque concentrad en su centro de gravedad, es decir, sin considerar el modelo masa-resorte. Este modelo es común en la práctica debido a su sencillez de aplicación.
Los valores máximos del momento de volteo en la cimentación del taque son casi iguales para ambos modelos hasta un periodo dominante del terreno de 1.4 s. Para periodos mayores el modelo M5 subestima el momento en la cimentación hasta en un 25%. Por lo anterior se recomienda considerar al menos tres masas para los modos convectivos y el efecto de rotación de la base del contenedor.
Conclusiones
En México recientemente se ha construido una gran cantidad de tanques elevados con formas arquitectónicas especiales que estructuralmente se comportan como péndulos invertidos, ya que están apoyados en un elemento lateral resistente y en los que el contenedor tiene forma cónica, paraboloide, esférica, o de paraguas. En estos sistemas estructurales el efecto debido al momento másico inercial del sistema contenedor-líquido puede ser importante en la respuesta sísmica de la estructura ya que puede inducir un momento de volteo en la cimentación mayor al que producen los modelos tradicionales propuestos en los códigos de diseño. La importancia de la rotación de la base del contenedor depende de la magnitud del momento másico inercial del sistema contenedor-líquido, de la rigidez rotacional del elemento lateral de apoyo y las características de la excitación sísmica.
Las ecuaciones propuestas en la Normas Técnicas Complementarias para el diseño y ejecución de obras e instalaciones hidráulicas (NTC-2004), así como en el Manual de Diseño de Obras Civiles (MDOC-2015) tienen su origen en un modelo simplificado para contenedores con paredes rígidas (Housner, 1957), además proponen considerar una masa para modelar el efecto impulsivo y otra para representa el modo convectivo. Implícitamente dichas ecuaciones consideran que el contenedor no presenta cabeceo. En este trabajo se presentan las ecuaciones generales de movimiento de un tanque elevado con forma arbitraria considerando el efecto por rotación en la base del contenedor. El modelo propuesto trata de complementar el modelo simplificado masa-resorte-amortiguador sugerido para el análisis sísmico de este tipo de estructuras en México.
Con el fin de realizar una aplicación de las ecuaciones propuestas se desarrolló un ejemplo de un tanque elevado con una geometría típica de los tanques de almacenamiento de agua utilizado en las alcaldías en la Ciudad de México y en diversos municipios del país. En dicho ejemplo la ecuación de movimiento se integró paso a paso para el registro sísmico presentado en el Valle de México durante el sismo de 1985 en la estación Central de Abasto (CA.EW). Los resultados muestran la importancia de considerar al menos tres masas convectivas para representar el oleaje del líquido. Aun cuando los desplazamientos del líquido son altos, el porcentaje de masa del líquido que representan es pequeño, lo que produce fuerzas cortantes relativamente pequeñas comparadas con la fuerza inercia total del sistema. Por otro lado, considerar la rotación de la base del contenedor puede incrementar el momento de volteo en la cimentación en un 15%.
Para el mismo ejemplo de aplicación y con el fin de definir los efectos de las condiciones dinámicas de la excitación se realizó un análisis modal utilizando los valores de aceleración espectral típicos en la Ciudad de México. Como resultado se obtuvo que los momentos de volteo en la cimentación se subestiman hasta en un 25% usando el modelo comúnmente empleado en la práctica profesional.











 nueva página del texto (beta)
nueva página del texto (beta)