1. INTRODUCTION
W UMa type stars are binaries of spectral type F0-K5 whose components have nearly equal surface temperatures and luminosities, despite their often greatly different masses (Binnendijk 1965). The model of Lucy (1968a, b) explained this effect by a common envelope (CE). The orbital motion of the two stellar components inside this envelope makes them lose angular momentum and eventually spiral towards each other (Webbink 1984, Qian 2003, Willems & Kolb 2004, Stepien 2006, Ivanova et al. 2013).
The PLC relationships of W UMa stars, combined with their ease of detection, make these binaries useful distance tracers (Klagyivik & Csizmadia 2004, Gettel et al. 2006, Eker et al. 2008). But the more important aspect of W UMa stars for modern astrophysics is that they provide information about the processes that drive tidal interactions, mass loss and mass transfer, angular momentum loss, and the merging of stars (Martin et al. 2011). Stellar mergers have been considered as a plausible origin of stellar eruptions of the V838 Mon (Munari et al. 2002) and V1309 Sco types (Rasio & Shapiro 1995, Tylenda et al. 2011, Zhu et al. 2016). However, the question of when the CE phase leads to the ejection of the envelope (and a tighter binary) and when to a star merger remains without answer. Hence, this short-lived phase is one of the most important unsolved problems in stellar evolution.
Developing a binary evolutionary model requires knowing the fundamental parameters of the components stars. W UMa binaries, especially those that undergo total eclipses, are the most important sources of such information. Moreover, the study of deep-contact binaries may throw light on the fate of all types of binaries.
This work presents photometric observations and light curve solutions of six deep-contact W UMa binaries: V0637 Peg (ASAS 222153+2802.8; GSC 02226-02148; UCAC4 591-134612; 2MASS J22215338+2802471), V0473 Cam (GSC 04530-01042; 2MASS J07170493+7710260; UCAC4 836-008955), CSS J153314.8+560527 (2MASS J15331471+5605280; UCAC4 731053285; GSC 03872-00076, and CSS J153314), CSS J075258.0+382035 (UCAC4 642042673, 2MASS J07513566+3820286, and CSS J075258), V0416 Gem (GSC 01356-02826; ASAS J065947+2229.9) and NSVS 6859986 (GSC 02397-00333; 2MASS J05114146+3531357; UCAC4 628-022051). Table 1 shows the coordinates of our observation targets and the information available on their light variability.
Table 1 Parameters of our observation targets taken from the VSX database
| Target | RA | Dec | Period [d] |
mag | Ampl [mag] |
Type |
| V0637 Peg | 22 21 53.40 | +28 02 47.0 | 0.311791 | 12.45(CV) | 0.77 | EW |
| V0473 Cam | 07 17 04.93 | +77 10 26.1 | 0.298438 | 11.55(R1) | 0.65 | EW |
| CSS J153314 | 15 33 14.71 | +56 05 28.2 | 0.264594 | 12.81(CV) | 0.47 | EW |
| CSS J075258 | 07 52 58.09 | +38 20 35.3 | 0.429914 | 13.07(CV) | 0.37 | EW |
| V0416 Gem | 06 59 47.31 | +22 29 48.6 | 0.256250 | 12.70(V) | 0.50 | EW |
| NSVS 6859986 | 05 11 40.85 | +35 31 33.2 | 0.38356914 | 12.40(R1) | 0.68 | EW |
2. OBSERVATIONS
The CCD photometric observations of the observation targets in the Sloan g ′ ,i ′ filters were performed at the Rozhen Observatory using the 30-cm Ritchey Chretien Astrograph (located in the IRIDA South dome) with an ATIK 4000 M CCD camera (2048 × 2048 pixels, 7.4µm/pixel, field of view 35 × 35 arcmin). Table 2 shows information of our observations.
Table 2 Log of our photometric observations
| Target | Date | Exposure (g' , i') [sec] |
Number (g' ,i') | Error (g' , i'′) [mag] |
| V0637 Peg | 2016 Sep 22 | 120, 120 | 62, 62 | 0.006, 0.008 |
| 2016 Sep 23 | 120, 120 | 79, 78 | 0.004, 0.006 | |
| 2016 Sep 24 | 120, 120 | 101, 99 | 0.006, 0.009 | |
| V0473 Cam | 2015 Jan 1 | 60, 90 | 120, 120 | 0.003, 0.003 |
| 2015 Jan 3 | 60, 90 | 39, 38 | 0.006, 0.006 | |
| CSS J153314 | 2016 Jun 20 | 120, 120 | 69, 68 | 0.007, 0.009 |
| 2016 Jun 21 | 120, 120 | 62, 62 | 0.006, 0.008 | |
| CSS J075258 | 2016 Feb 9 | 180, 240 | 38, 39 | 0.003, 0.006 |
| 2016 Feb 15 | 180, 240 | 63, 62 | 0.004, 0.006 | |
| 2016 Feb 28 | 180, 240 | 35, 34 | 0.004, 0.007 | |
| 2016 Mar 6 | 180, 240 | 36, 34 | 0.003, 0.006 | |
| 2016 Feb 17 | 180, 240 | 48, 48 | 0.004, 0.006 | |
| 2016 Feb 18 | 180, 240 | 59, 58 | 0.006, 0.008 | |
| V0416 Gem | 2016 Dec 3 | 60, 90 | 48, 48 | 0.010, 0.013 |
| 2016 Dec 4 | 60, 90 | 85, 85 | 0.005, 0.006 | |
| 2016 Dec 5 | 60, 90 | 125, 125 | 0.005, 0.006 | |
| 2016 Dec 6 | 60, 90 | 31, 31 | 0.005, 0.006 | |
| 2016 Dec 8 | 60, 90 | 32, 32 | 0.005, 0.007 | |
| 2016 Dec 9 | 60, 90 | 87, 87 | 0.005, 0.007 | |
| 2016 Dec 10 | 60, 90 | 165, 165 | 0.005, 0.007 | |
| NSVS 6859986 | 2016 Nov 24 | 60, 90 | 132, 132 | 0.004, 0.005 |
| 2016 Nov 25 | 60, 90 | 91, 91 | 0.004, 0.006 | |
| 2016 Nov 27 | 60, 90 | 139, 139 | 0.009, 0.011 |
The data were obtained during photometric nights with seeing in the range of 1.1-1.9 arcsec. The airmass of the observations of all targets was within the range 1.01-2.01. Twilight flat fields were obtained through each filter, as well as dark and bias frames. The frames were combined into a single master bias, and dark and flat frames. The reduction of the photometric data was done using the standard procedure (de-biasing, dark-frame subtraction and flat-fielding) with the software AIP4WIN v.2.0 (Berry & Burnell 2006).
For the stellar images, we used aperture photometry with a radius of 1.5 FWHM as well as sky background measurements in an annulus encompassing a comparable area. The light variability of the observation targets was estimated by comparing it with nearby (constant) stars in the observed field of each target (ensemble photometry). A check star served to determine the observational accuracy and to verify the constancy of the comparison stars. CCD ensemble photometry calculates the difference between the instrumental magnitude of the target and a comparison magnitude obtained from the mean of the intensities of the chosen comparison stars. The use of numerous comparison stars increases considerably the statistical accuracy of the comparison magnitude (Gilliland & Brown 1988, Honeycutt 1992).
We performed the ensemble aperture photometry with the software VPHOT (https://www.aavso.org/vphot). Table 3 shows the coordinates of the comparison and check stars, taken from the UCAC4 catalogue (Zacharias et al. 2013); their magnitudes were taken from the APASS DR9 catalogue (Henden et al. 2016). According to the VSX database, the stars CSS J153314.8+560527 and NSVS 2808700 are very close in position and have almost equal periods. Our observations revealed that the second star is not variable.
Table 3 List of the standard stars
| Label | Star ID | RA | Dec | g′ | i′ |
| Target | V0637 Peg | 22 21 53.40 | +28 02 47.00 | 13.24 | 12.24 |
| Chk | UCAC4 591-134602 | 22 21 47.14 | +28 05 28.21 | 14.360 | 13.201 |
| C1 | UCAC4 590-134319 | 22 21 58.53 | +27 57 39.13 | 13.700 | 13.190 |
| C2 | UCAC4 590-134268 | 22 21 27.93 | +27 58 29.23 | 14.206 | 13.301 |
| C3 | UCAC4 590-134302 | 22 21 48.22 | +27 59 26.26 | 13.982 | 13.359 |
| C4 | UCAC4 591-134550 | 22 21 15.51 | +28 04 13.34 | 13.539 | 12.884 |
| C5 | UCAC4 591-134590 | 22 21 38.84 | +28 05 26.42 | 13.229 | 12.297 |
| C6 | UCAC4 591-134573 | 22 21 31.08 | +28 07 20.65 | 13.213 | 12.615 |
| C7 | UCAC4 591-134594 | 22 21 41.55 | +28 08 12.48 | 13.318 | 12.713 |
| C8 | UCAC4 591-134609 | 22 21 51.23 | +28 08 03.18 | 13.773 | 13.106 |
| C9 | UCAC4 591-134625 | 22 21 59.90 | +28 05 28.35 | 13.329 | 12.661 |
| C10 | UCAC4 590-134318 | 22 21 57.52 | +27 55 26.19 | 13.479 | 12.254 |
| Target | V0473 Cam | 07 17 04.93 | +77 10 26.10 | 11.860 | 11.101 |
| Chk | UCAC4-837-008887 | 07 17 11.21 | +77 12 38.47 | 12.231 | 11.248 |
| C1 | UCAC4-837-008919 | 07 19 47.76 | +77 17 47.18 | 12.650 | 12.049 |
| C2 | UCAC4-837-008907 | 07 18 47.34 | +77 18 04.02 | 12.386 | 11.084 |
| C3 | UCAC4-837-008861 | 07 15 04.93 | +77 17 40.46 | 12.664 | 11.738 |
| C4 | UCAC4-837-008897 | 07 18 12.24 | +77 15 46.18 | 13.047 | 11.812 |
| C5 | UCAC4-836-008980 | 07 19 10.50 | +77 10 27.41 | 13.049 | 12.201 |
| C6 | UCAC4-836-008968 | 07 18 01.77 | +77 11 57.23 | 12.428 | 11.966 |
| C7 | UCAC4-836-008948 | 07 16 26.49 | +77 05 33.45 | 13.243 | 12.059 |
| C8 | UCAC4-836-008929 | 07 15 08.62 | +77 09 09.54 | 12.003 | 11.303 |
| Target | CSS J153314 | 15 33 14.71 | +56 05 28.25 | 12.981 | 12.076 |
| Chk | UCAC4 731-053305 | 15 34 24.40 | +56 04 59.16 | 14.041 | 12.736 |
| C1 | UCAC4 731-053289 | 15 33 23.47 | +56 05 26.31 | 12.567 | 11.645 |
| C2 | UCAC4 731-053282 | 15 33 03.52 | +56 07 03.97 | 13.202 | 12.249 |
| C3 | UCAC4 731-053294 | 15 33 38.81 | +56 10 18.03 | 12.473 | 11.881 |
| C4 | UCAC4 731-053302 | 15 34 05.08 | +56 02 54.73 | 12.803 | 12.067 |
| C5 | UCAC4 730-053151 | 15 33 43.32 | +55 59 24.05 | 12.976 | 12.507 |
| C6 | UCAC4 730-053123 | 15 32 23.54 | +55 56 07.04 | 11.544 | 11.043 |
| C7 | UCAC4 732-053671 | 15 33 00.50 | +56 15 00.72 | 10.806 | 9.762 |
| Target | CSS J075258 | 07 52 58.09 | +38 20 35.30 | 13.205 | 12.746 |
| Chk | UCAC4 643-044185 | 07 51 20.51 | +38 34 24.58 | 14.121 | 13.686 |
| C1 | UCAC4 643-044208 | 07 51 47.59 | +38 35 55.44 | 14.120 | 13.657 |
| C2 | UCAC4 643-044212 | 07 51 49.87 | +38 35 24.70 | 14.660 | 13.681 |
| C3 | UCAC4 643-044217 | 07 51 54.27 | +38 32 17.07 | 14.572 | 13.818 |
| C4 | UCAC4 643-044225 | 07 52 03.85 | +38 32 23.81 | 14.709 | 14.018 |
| C5 | UCAC4 643-044233 | 07 52 15.03 | +38 31 48.84 | 13.911 | 13.311 |
| C6 | UCAC4 643-044248 | 07 52 40.64 | +38 32 08.27 | 14.134 | 13.686 |
| C7 | UCAC4 643-044271 | 07 53 09.97 | +38 31 21.83 | 13.671 | 13.366 |
| C8 | UCAC4 643-044218 | 07 51 54.46 | +38 29 44.02 | 14.346 | 13.859 |
| Target | V0637 Peg | 22 21 53.40 | +28 02 47.00 | 13.24 | 12.24 |
| Chk | UCAC4 591-134602 | 22 21 47.14 | +28 05 28.21 | 14.360 | 13.201 |
| C1 | UCAC4 590-134319 | 22 21 58.53 | +27 57 39.13 | 13.700 | 13.190 |
| C2 | UCAC4 590-134268 | 22 21 27.93 | +27 58 29.23 | 14.206 | 13.301 |
| C3 | UCAC4 590-134302 | 22 21 48.22 | +27 59 26.26 | 13.982 | 13.359 |
| C4 | UCAC4 591-134550 | 22 21 15.51 | +28 04 13.34 | 13.539 | 12.884 |
| C5 | UCAC4 591-134590 | 22 21 38.84 | +28 05 26.42 | 13.229 | 12.297 |
| C6 | UCAC4 591-134573 | 22 21 31.08 | +28 07 20.65 | 13.213 | 12.615 |
| C7 | UCAC4 591-134594 | 22 21 41.55 | +28 08 12.48 | 13.318 | 12.713 |
| C8 | UCAC4 591-134609 | 22 21 51.23 | +28 08 03.18 | 13.773 | 13.106 |
| C9 | UCAC4 591-134625 | 22 21 59.90 | +28 05 28.35 | 13.329 | 12.661 |
| C10 | UCAC4 590-134318 | 22 21 57.52 | +27 55 26.19 | 13.479 | 12.254 |
| Target | V0473 Cam | 07 17 04.93 | +77 10 26.10 | 11.860 | 11.101 |
| Chk | UCAC4-837-008887 | 07 17 11.21 | +77 12 38.47 | 12.231 | 11.248 |
| C1 | UCAC4-837-008919 | 07 19 47.76 | +77 17 47.18 | 12.650 | 12.049 |
| C2 | UCAC4-837-008907 | 07 18 47.34 | +77 18 04.02 | 12.386 | 11.084 |
| C3 | UCAC4-837-008861 | 07 15 04.93 | +77 17 40.46 | 12.664 | 11.738 |
| C4 | UCAC4-837-008897 | 07 18 12.24 | +77 15 46.18 | 13.047 | 11.812 |
| C5 | UCAC4-836-008980 | 07 19 10.50 | +77 10 27.41 | 13.049 | 12.201 |
| C6 | UCAC4-836-008968 | 07 18 01.77 | +77 11 57.23 | 12.428 | 11.966 |
| C7 | UCAC4-836-008948 | 07 16 26.49 | +77 05 33.45 | 13.243 | 12.059 |
| C8 | UCAC4-836-008929 | 07 15 08.62 | +77 09 09.54 | 12.003 | 11.303 |
| Target | CSS J153314 | 15 33 14.71 | +56 05 28.25 | 12.981 | 12.076 |
| Chk | UCAC4 731-053305 | 15 34 24.40 | +56 04 59.16 | 14.041 | 12.736 |
| C1 | UCAC4 731-053289 | 15 33 23.47 | +56 05 26.31 | 12.567 | 11.645 |
| C2 | UCAC4 731-053282 | 15 33 03.52 | +56 07 03.97 | 13.202 | 12.249 |
| C3 | UCAC4 731-053294 | 15 33 38.81 | +56 10 18.03 | 12.473 | 11.881 |
| C4 | UCAC4 731-053302 | 15 34 05.08 | +56 02 54.73 | 12.803 | 12.067 |
| C5 | UCAC4 730-053151 | 15 33 43.32 | +55 59 24.05 | 12.976 | 12.507 |
| C6 | UCAC4 730-053123 | 15 32 23.54 | +55 56 07.04 | 11.544 | 11.043 |
| C7 | UCAC4 732-053671 | 15 33 00.50 | +56 15 00.72 | 10.806 | 9.762 |
| Target | CSS J075258 | 07 52 58.09 | +38 20 35.30 | 13.205 | 12.746 |
| Chk | UCAC4 643-044185 | 07 51 20.51 | +38 34 24.58 | 14.121 | 13.686 |
| C1 | UCAC4 643-044208 | 07 51 47.59 | +38 35 55.44 | 14.120 | 13.657 |
| C2 | UCAC4 643-044212 | 07 51 49.87 | +38 35 24.70 | 14.660 | 13.681 |
| C3 | UCAC4 643-044217 | 07 51 54.27 | +38 32 17.07 | 14.572 | 13.818 |
| C4 | UCAC4 643-044225 | 07 52 03.85 | +38 32 23.81 | 14.709 | 14.018 |
| C5 | UCAC4 643-044233 | 07 52 15.03 | +38 31 48.84 | 13.911 | 13.311 |
| C6 | UCAC4 643-044248 | 07 52 40.64 | +38 32 08.27 | 14.134 | 13.686 |
| C7 | UCAC4 643-044271 | 07 53 09.97 | +38 31 21.83 | 13.671 | 13.366 |
| C8 | UCAC4 643-044218 | 07 51 54.46 | +38 29 44.02 | 14.346 | 13.859 |
The transformation of the instrumental magnitudes into standard ones was done manually. For this, we used the mean color of the ensemble comparison star
Tables 8-13 in the Appendix show the templates derived from our photometric data (full tables are available at the CDS, /CatS/217.174.158.82 : 004.)
3. LIGHT CURVE SOLUTIONS
The IRIDA light curves of the observation targets were solved using the PHOEBE code (Prsa & Zwitter, 2005), which is based on the Wilson-Devinney (WD) code (Wilson & Devinney 1971, Wilson 1979, 1993) but has some improvements such as a graphical user interface and updates such as the Sloan filters used in our observations.
The target temperatures T m were determined (Table 5) from their infrared color indices (J-K), taken from the 2MASS catalog, and the colortemperature calibration of Tokunaga (2000).
Table 4 Values of the fitted parameters
| Star | T 0 | Ω | q | i | T 2 |
| V0637 Peg | 2457372.21954(5) | 2.73(3) | 0.501(1) | 88(4) | 4587(32) |
| V0473 Cam | 2457024.41640(3) | 2.66(2) | 0.47(3) | 84.7(8) | 5100(41) |
| CSS J153314 | 2457560.42347(7) | 5.7(3) | 2.6(2) | 86(1) | 4933(567) |
| CSS J075258 | 2457434.43750(8) | 9.5(2) | 5.6(1) | 84.3(6) | 6070(23) |
| V0416 Gem | 2457726.45333(9) | 10.8(2) | 6.7(2) | 73.2(7) | 5420(294) |
| NSVS 6859986 | 2457718.50448(9) | 8.3(3) | 4.8(3) | 89(1) | 5100(680) |
Table 5 Calculated parameters
| Star | Tm |
|
|
r 1 | r 2 | f | l2/l1 |
| V0637 Peg | 4903 | 4997(50) | 4681(40) | 0.479(1) | 0.361(1) | 0.504 | 0.429 |
| V0473 Cam | 5300 | 5361(50) | 5161(60) | 0.487(1) | 0.357(1) | 0.539 | 0.459 |
| CSS J153314 | 4933 | 4933(567) | 4933(567) | 0.340(1) | 0.504(2) | 0.566 | 2.268 |
| CSS J075258 | 6203 | 6227(60) | 6094(50) | 0.273(1) | 0.560(2) | 0.630 | 3.851 |
| V0416 Gem | 5420 | 5420(294) | 5420(294) | 0.259(1) | 0.573(2) | 0.651 | 5.058 |
| NSVS 6859986 | 5100 | 5100(616) | 5100(616) | 0.302(1) | 0.560(2) | 0.864 | 3.756 |
The initial runs revealed that all observation targets are overcontact systems. Thus, we used the “Overcontact Binary not in Thermal Contact” mode of the code. The fit quality was estimated based on the value χ 2.
First, we fixed T 1 = T m and varied the initial epoch T 0 and period P to fit the light curves to the phases of light minima and maxima. Afterwards, we fixed T 0 and P, and varied simultaneously the secondary temperature T 2, the orbital inclination i, the mass ratio q and the potential Ω to try to reproduce complete light curves. The data in the i ′ and g ′ bands were modelled simultaneously.
We used gravity brightening coefficients of g 1 = g 2 = 0.32 and reflection effect coefficients of A 1 = A 2 = 0.5, which are appropriate for late-type stars; the linear limb-darkening coefficients for each component and each color were updated according to the tables of Van Hamme (1993). Solar metallicity was assumed for the targets because they consist of late stars from the solar vicinity.
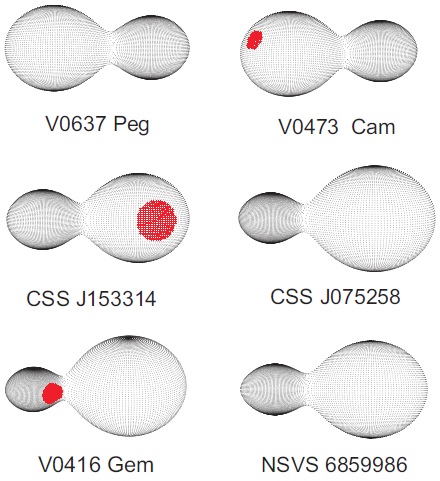
In order to reproduce the light curve anomalies, we used cool spots. Varying the parameters of these spots (longitude λ, angular size α and temperature factor κ) simultaneously with the other configuration parameters often led to non-physical values. This is why the spot parameters were adjusted “manually” (within reasonable ranges). Due to the ambiguousness of the solution of the inverse problem, we chose almost equatorial spots on the primary stars because they have the smallest size and temperature contrast required to fit a given light curve distortion.
After finding the best solution we varied all parameters together (T 2, i, q, Ω, T 0 and P) around the values from the last run and obtained the final model.
In order to adjust the stellar temperatures
where c = l 2 /l 1 (luminosity ratio) and ∆T = T m −T 2 were taken from the final PHOEBE fit.
Although PHOEBE (as well as WD) works with potentials, it allows to calculate directly the values (polar, point, side, and back) of the relative radius r
i
= R
i
/a of each component (R
i
is the linear radius and a is orbital separation). In the absence of radial velocity curves, we chose as default a = 1. Moreover, PHOEBE yields the bolometric magnitudes
Table 4 shows the final values of the fitted stellar parameters and their uncertainties: initial epoch T 0; mass ratio q; inclination i; potential Ω; secondary temperature T 2. The mass ratios correspond to the ratio between the mass of the primary component and the mass of the star eclipsed at MinI. The orbital periods P from Table 1 fitted our data well.
Table 5 shows the following calculated parameters: stellar temperatures
Table 6 Parameters of the surface spots
| star |
β [o] |
λ [o] |
α [o] |
k |
| V0473 Cam | 70(5) | 200(2) | 12(0.5) | 1.1(0.1) |
| CSS J153314 | 90(5) | 100(2) | 25(1) | 0.9(0.1) |
| V0416 Gem | 90(5) | 310(2) | 24(1) | 0.8(0.1) |
The synthetic light curves corresponding to our solutions are shown in Figure 1 as continuous lines. At most phases, the residuals do not affect the observational precision (see Table 1) but they are larger during the eclipses of some targets (especially the primary eclipses of V0637 Peg and V0473 Cam). Attempts to improve the fits by introducing nonlinear limb-darkening laws (logarithmic and square root) and arbitrarily varying the limb-darkening coefficients arbitrary were unsuccessful. We suspect that the reason for this are numerical imprecisions in the physical model of deep-contact binaries. It should be pointed out that this behavior of the residual curves can be observed even in some Kepler binaries (Hambleton et al. 2013, Lehmann et al. 2013, Maceroni et al. 2014). Kipping (2010) attributed it to the effects of finite integration time, while Prsa et al. (2016) attributed it to an inadequate treatment of overcontact binaries, especially of their neck regions.
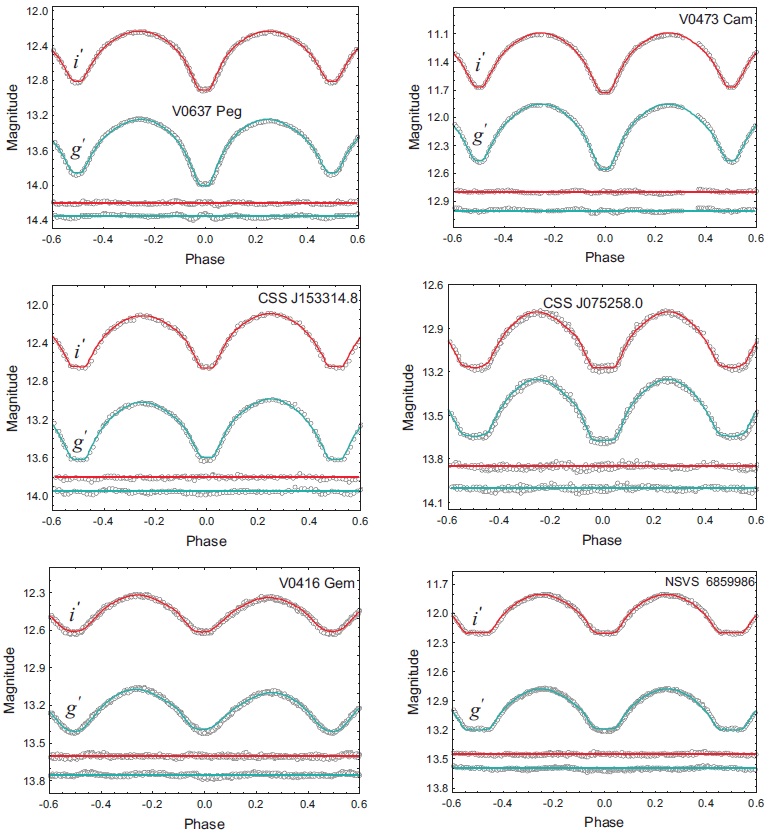
Fig. 1 The folded light curves of the observation targets with their fits and residuals (shifted vertically by different amounts to save space).
The main results of our model are as follows: (i) All observation targets undergo total eclipses, which means that their photometric mass ratios can be determined with great confidence (Terrell & Wilson 2005); (ii) the components of each target are almost equal in temperature and are of the G and K spectral types (Table 5); (iii) All targets have deep-contact configurations (Figure 2, Table 5) with a fill-out factor f > 0.5 that reaches f = 0.84 for NSVS 6859986; (iv) The values of l 2 /l 1 ,q,r 2 /r 1 shown in Tables 4- 5 confirm the assumption that the luminosity ratio for deep-contact binaries (whose components have equal temperatures) depends on the squared ratio of the components’ radii but not on the mass ratio. This means that the empirical relation between the global parameters of deep-contact binaries are different from those of MS stars.
4. DEEP-CONTACT BINARIES
In order to study the dependencies between the fill-out factor and the stellar parameters of deepcontact systems, as well as to verify if they correspond to theoretical predictions, we performed a statistical analysis of our targets and several tens of well studied overcontact systems (Table 7). For targets with q > 1, we changed the order of the components, which means that: (i) the mass ratios were substituted by their inverse values; (ii) the luminosity ratios were substituted by their inverse values; (iii) the relative radii and temperatures of the stellar components were exchanged for each other. For targets with more than one solution, we used the newest one (e.g. FG Hya).
Table 7 Parameters of deep-contact binaries sorted by increasing fillout factor
| star | Tm | P | q | Ω | r 1 | r 2 | f | l2/l1 | Ref |
| DN Cam | 6600 | 0.498 | 0.442 | 5.319 | 0.523 | 0.39 | 0.33 | 0.53 | 1 |
| EK Com | 5200 | 0.267 | 0.35 | 2.501 | 0.523 | 0.344 | 0.33 | 0.449 | 2 |
| EX Leo | 6200 | 0.408 | 0.2 | 2.186 | 0.545 | 0.257 | 0.35 | 0.206 | 3 |
| FP Boo | 6600 | 0.640 | 0.096 | 1.922 | 0.631 | 0.247 | 0.38 | 0.105 | 4 |
| BX Dra | 7100 | 0.579 | 0.28 | 2.351 | 0.518 | 0.287 | 0.41 | 0.363 | 3 |
| V902 Sgr | 5200 | 0.294 | 0.13 | 2.019 | 0.606 | 0.271 | 0.43 | 0.176 | 5 |
| AQ Psc | 6100 | 0.476 | 0.231 | 2.244 | 0.565 | 0.323 | 0.44 | 0.352 | 4 |
| OU Ser | 6100 | 0.297 | 0.172 | 2.113 | 0.562 | 0.248 | 0.44 | 0.263 | 6 |
| V1918 Cyg | 7000 | 0.413 | 0.264 | 2.303 | 0.559 | 0.340 | 0.49 | 0.298 | 7 |
| V0637 Peg | 4903 | 0.311 | 0.50 | 2.727 | 0.479 | 0.361 | 0.50 | 0.429 | 8 |
| V839 Oph | 6300 | 0.409 | 0.294 | 2.357 | 0.554 | 0.355 | 0.53 | 0.453 | 4 |
| V0473 Cam | 5300 | 0.298 | 0.47 | 2.659 | 0.487 | 0.357 | 0.54 | 0.459 | 8 |
| ET Leo | 5300 | 0.346 | 0.342 | 6.178 | 0.545 | 0.372 | 0.55 | 0.432 | 4 |
| CSS J153314 | 4933 | 0.265 | 0.39 | 5.71 | 0.504 | 0.340 | 0.57 | 0.441 | 8 |
| V592 Per | 6400 | 0.716 | 0.389 | 2.526 | 0.498 | 0.325 | 0.59 | 0.275 | 6 |
| IK Per | 8800 | 0.676 | 0.171 | 2.094 | 0.597 | 0.313 | 0.60 | 0.19 | 9 |
| NN Vir | 6900 | 0.481 | 0.487 | 2.674 | 0.529 | 0.418 | 0.61 | 0.555 | 10 |
| CSS J075258 | 6203 | 0.430 | 0.18 | 9.54 | 0.560 | 0.273 | 0.63 | 0.26 | 8 |
| Y Sex | 6100 | 0.420 | 0.18 | 0.563 | 0.283 | 0.64 | 11 | ||
| V0416 Gem | 5420 | 0.256 | 0.148 | 10.84 | 0.573 | 0.259 | 0.65 | 0.198 | 8 |
| V1191 Cyg | 6500 | 0.313 | 0.107 | 1.933 | 0.634 | 0.281 | 0.69 | 0.163 | 12 |
| FG Hya | 6300 | 0.328 | 0.104 | 1.924 | 0.614 | 0.22 | 0.69 | 0.179 | 3 |
| ASAS J082243 | 6600 | 0.28008 | 0.106 | 0.72 | 13 | ||||
| V410 Aur | 5900 | 0.366 | 0.137 | 2.004 | 0.618 | 0.304 | 0.72 | 0.227 | 4 |
| AH Aur | 6300 | 0.494 | 0.165 | 2.064 | 0.608 | 0.327 | 0.75 | 0.25 | 10 |
| V776 Cas | 6700 | 0.440 | 0.138 | 2.001 | 0.595 | 0.244 | 0.77 | 0.19 | 6 |
| TV Mus | 5900 | 0.446 | 0.15 | 0.568 | 0.278 | 0.77 | 14, 15 | ||
| DZ Psc | 6200 | 0.366 | 0.145 | 2.015 | 0.618 | 0.322 | 0.79 | 0.21 | 10 |
| V728 Her | 6670 | 0.471 | 0.158 | 2.024 | 0.581 | 0.293 | 0.81 | 0.33 | 16 |
| AW UMa | 7100 | 0.439 | 0.09 | 0.619 | 0.228 | 0.85 | 0.11 | 17, 18 | |
| NSVS 6859986 | 5100 | 0.383 | 0.209 | 8.33 | 0.560 | 0.302 | 0.86 | 0.26 | 8 |
| CK Boo | 6150 | 0.355 | 0.106 | 1.915 | 0.641 | 0.303 | 0.91 | 0.25 | 4 |
| GR Vir | 6300 | 0.347 | 0.106 | 1.913 | 0.645 | 0.317 | 0.93 | 0.20 | 10 |
References: 1- Baran et al. 2004; 2 - Deb et al. 2010; 3 - Zola et al. 2010; 4 - Gazeas et al. 2006; 5 - Samec & Corbin 2002; 6 - Zola et al. 2005; 7 - Yang et al. 2013; 8 - this paper; 9 - Zhu et al. 2005; 10 - Gazeas et al. 2005; 11 - Yang & Liu 2003; 12 - Zhu et al. 2011; 13 - Kandulapati et al. 2015; 14 - Maceroni & van’t Veer 1996; 15 - Qian et al. 2005; 16 - Erkan & Ulas 2016; 17 - Yang 2008; 18 - Rucinski 2015.
The diagrams of the relationships between the fill-out factor and the -configuration parameters (Figure 3) show rather scattered distributions that cannot be fitted to any function. However, we were able to identify some qualitative tendencies.
The fill-out factor f seems not to depend on stellar temperature.
A tendency of f to increase with decreasing periods P corresponds to theoretical predictions. But there are deviations from this tendency; for instance, EK Com has a period of 0.27 days and f =0.33.
The fill-out factor increases as the mass ratio decreases, in agreement with theoretical predictions. But there are deviations from this tendency; for instance, FP Boo has q ≈ 0.1 and a moderate fill-out factor of 0.38 (Figure 3).
We found a tendency for f to increase as the primary radius r 1 increases.
The fill-out factor tends to increase as the secondary radius r 2 decreases, and also as the luminosity ratio l 2 /l 1 decreases (Figure 3).
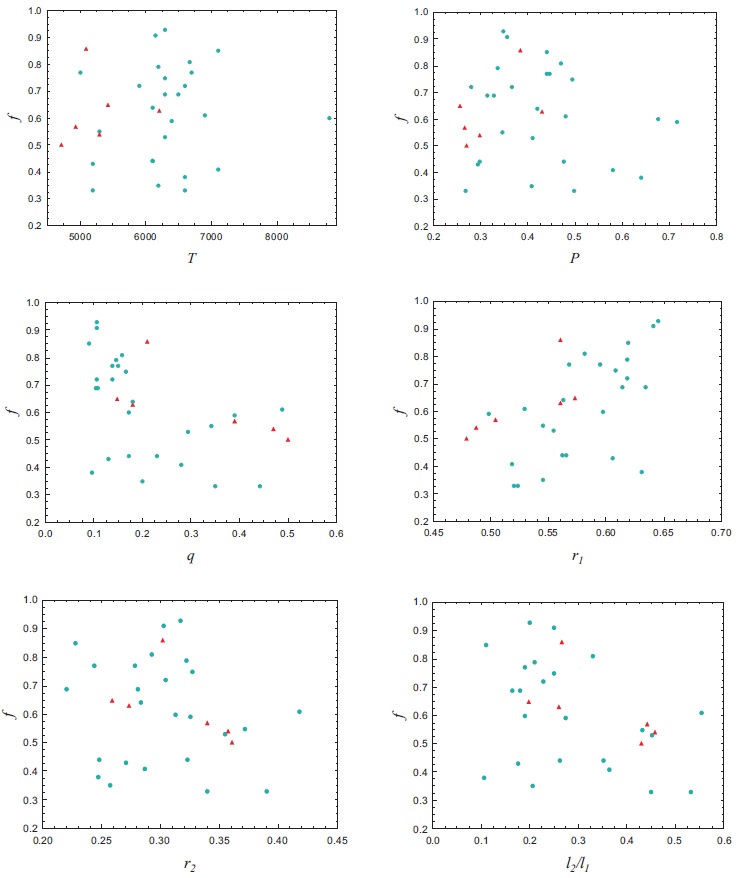
Fig. 3 Empirical relationships between the fill-out factor and stellar parameters (the red triangles indicate our targets; the blue circles indicate for other overcontact systems from Table 7). The color figure can be viewed online.
These tendencies are in agreement with the expected physically relationships, but there are deviations from them, especially for moderate values of f (Figure 3).
This analysis leads to the question of which of the targets shown Figure 3 will become progenitors of tight binaries and which will merge. Or is there another evolutionary outcome?
5. CONCLUSION
Our observations and light curve solutions showed that V0637 Peg, V0473 Cam, CSS J153314, CSS J075258, V0416 Gem and NSVS 6859986 have deeply overcontact configurations with fill-out factors above 0.5. The components of all the observation targets have almost equal temperatures and undergo total eclipses.
We studied the dependencies between the fill-out factor and stellar parameters (temperature, period, relative stellar radii, mass ratio, luminosity ratio) in a sample of three dozens deep-contact binaries. Most of them are consistent with theoretical predictions of the evolutionary scenarios but there are deviations from the common tendencies.
This study adds estimated parameters for six new deep-contact systems to the family of W UMa binaries. The statistical analysis of the dependencies between the fill-out factor and the stellar parameters of deep-contact systems opens new questions about the evolutionary fate of such configurations.
This work was supported partly by project HD08/20 of the Foundation for Scientific Research of the Bulgarian Ministry of Education and Science as well as by project RD 08-102 of Shumen University. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research also makes use of the SIMBAD database, operated at CDS, Strasbourg, France, the NASA Astrophysics Data System Abstract Service, the USNOFS Image and Catalogue Archive operated by the United States Naval Observatory, the Flagstaff Station (http://www.nofs.navy.mil/data/fchpix/) and the photometric software VPHOT operated by the AAVSO, Cambridge, Massachusetts (https://www.aavso.org/vphot). The authors are very grateful to the anonymous referee for the valuable suggestions and notes.











 nueva página del texto (beta)
nueva página del texto (beta)