1. Introduction
The evolution of extragalactic radio sources (EGRSs) in the universe to their present sizes or between different cosmological epochs is of great importance in the study of their unification schemes. This provides information on the nature of the radio source together with its environment over cosmological epochs, as well as on the “nature” (energy flowing out of the central engine along the beam) and “nurture” (the density or pressure of gas surrounding the sources) alternatives. “Nature” and “nurture” are believed to govern the size evolution of extragalactic radio sources (Smolcic et al., 2009). In these effects, the radio sizes are expected to depend on the product of a number of independent variables. Unification schemes are the theoretical frameworks in which different classes of EGRSs are explained as being derived from the same parent population; observations at varying orientations and/or different cosmological epochs give rise to the apparent differences.
The cosmological evolution model argues that the similarities and/or differences in the observed properties of a given sample of EGRSs are due to evolution of the source parameters with cosmological epoch, defined by the redshift (z). There is a change in the observed physical size with cosmological epoch as well as a linear size redshift/radio luminosity (D − z/P ) correlation in the relativistic phase for the source angular diameter. The cosmological evolution of both the radio size and luminosity can be used to interpret the observed angular size redshift (θ − z ) data of extragalactic radio sources. Several research works have been carried out on this evolution scenario using different samples of radio sources and, in consequence, apparently inconsistent results have been obtained.
It has been argued (Miley, 1968; Okoye & Onuora, 1982) that for radio galaxies and quasars to be unified, the observed θ − z relationship of radio sources can be interpreted by a θ − z−1 relation. Alternatively, the data can be effective with a linear size luminosity correlation (Masson, 1980). In this sense, Okoye and Onuora (1982) suggested a linear size (D) evolution of the form D ≈ (1 + z)k, depending on the value of the density parameter (Ω0). They reported a value of the linear size evolution parameter k in the range of 1 ≤ k ≤ 2, for both radio galaxies and quasars and opined that both extended steep spectrum (ESS) radio galaxies and quasars undergo similar size evolution. Oort et al (1987) obtained a steeper linear size evolution in radio galaxies with k = 3. Ubachukwu (1995) studied the implications of intrinsic luminosity evolution with cosmological epoch on the value of the density parameter (Ω0) and evolution of radio sizes of EGRS and suggested that a power law luminosity evolution model of the form P ≈ (1 + z)β could be used to constrain the value of Ω0. In fact, the author argued that, with a strong luminosity evolution, the model yielded an upper limit of Ω0 ≈ 0.5 Blundell et al. (1999) studied the trends in luminosity, linear size, spectral index and redshift of classical double radio sources from three complete samples selected at successively fainter low radio frequency flux limits. They decoupled the effects of the tight correlation between redshift and luminosity, which have hindered the interpretation of the relationships between these four properties, and found that spectral indices increased with linear size, with a stronger dependence on radio luminosity than on redshift, except at high gigahertz (GHz) frequencies. Furthermore, the authors found that linear sizes decreased at higher redshift and argued that there was an energy loss mechanism which caused decreasing luminosity through the life of a source and hence, suggested a “youth-redshift degeneracy” model for these sources.
On the other hand, Snellen et al. (2000) predicted that there was a difference in slope of gigahertz peaked spectrum (GPS) luminosity functions due to the luminosity evolution of the individual sources and argued that this in turn affected the cosmological evolution of the objects. They suggested that GPS sources had a strong positive (β > 0) luminosity evolution, while large-scale sources had a negative (β < 0) luminosity evolution. Goodlet & Kaiser (2005) investigated trends of the polarization properties with fundamental parameters such as radio redshift, luminosity and linear size. They found a weak anti-correlation between radio luminosity and the linear size of the inclusive sample and concluded that radio-loud AGNs at high radio luminosity were located in more turbulent environments than their low-luminosity counterparts. More recently, Aird et al. (2010) studied the luminosity-linear size (P - D) track of EGRSs and found that the evolution parameter appeared to differ remarkably over wide redshift regimes. In particular, Massardi et al. (2010) argued that negative evolution occured mostly in high redshift sources. Drawing from all these studies, it can therefore be concluded that both linear size and luminosity of EGRSs undergo some forms of cosmological evolution and, perhaps, in turn, could be used to interpret the data of radio sources.
In this paper, we interpret the observed θ − z data of radio sources in terms of combined effects of linear size evolution, temporal evolution, luminosity selection and source orientation.
The sample used in the paper is based on the large database of 1038 edge-brightened double EGRSs taken from Nilsson (1998). The sample of Nilsson (1998) is composed of two major sub-classes of the EGRSs, namely, 365 quasars and 544 radio galaxies, with 129 optically unidentified objects. However, out of the 909 identified objects, there are 486 sources whose properties have been defined as Compact Steep Spectrum (CSS) (e.g Ubachukwu, 1995) with D ≤ 15kpc; α > 0.5, P178M H z ≥ 1025 WHz−1 . These CSS sources and the 129 unidentified objects were excluded from the present study, since they are believed to belong to a different class of objects with different cosmic evolution. This was done in order to minimize any bias which their presence could introduce into the analyses. It has been suggested (e.g Van Breudel et al., 1984) that the combination of compactness and steep spectrum in the CSS objects was indeed due to a strong interaction of the emitting plasma with the intergalactic medium. Fanti et al. (1990) and Saikia et al. (1995) argued that CSS small nature appears to be determined by their environments rather than by orientation. Thus, there are 423 objects in the final sample, comprising 173 galaxies and 250 quasars. Nilsson (1998) provides flux information on the extended radio lobes and the core components, overall linear extent and structural asymmetry parameter of the objects in the sample, assuming H0 = 50 kms−1 Mpc−1 and Ω0 = 1.0 cosmology. However, for the analysis in this paper, all information has been adjusted to the current value of the Hubble’s parameter: H0 = 70 kms−1 Mpc−1. Similarly, all radio luminosity values have been converted to the standard unit of WHz−1. In § 2, the angular size - redshift (θ−z) relation of radio sources is studied. Pure linear size evolution with cosmic epoch is discussed in § 3, while § 4 examines the effects of luminosity and temporal evolution. The radio source orientation paradigm is studied in § 5 and finally, § 6 discusses the results.
2. Angular size - redshift (θ-Z) relation
The angular size - redshift (θ z) relation of radio sources has been widely accepted in explaining the evolution of extragalactic radio sources in an expanding universe (e.g. Donoso et al. 2009). This relation derives from the fact that the apparent angular size of a source depends on some independent variables via luminosity, distance, and the geometry of the universe. In the Friedmann-Robertson- Walker universe, the angular size - redshift (θ z) relation of radio sources is given (e.g. Miley, 1968) as
where D is the linear size expressed in kpc and dL is the luminosity distance which depends on H0 and Ω0 according to the relation (e.g. Mattig, 1959):
with c being the speed of light. Using Equation (2) in (1), assuming the simplest cosmology for a matter dominated universe with Ω0 = Ωm = ΩΛ, where ΩΛ = 0, we have,
Equation (3) implies that for z < 1, θ decreases with increasing z, while at z > 1, θ increases with increasing z. In standard cosmology, the apparent angular size (θ) of a radio source of proper linear size (D), is expected to decrease with increasing redshift (z) reaching a minimum at a certain value of z, depending on the value of density parameter (Ω0) and to increase thereafter. This relation has been severally used in the past to constrain Ω0 for an assumed value of the Hubble parameter (e.g. Okoye and Onuora 1982; Ubachukwu 1995).
To investigate the θ − z data of the current sample in the context of the inflationary universe, the scatter plot of θ as a function of z is shown in Figure 1. However, Kapahi (1989) has shown that, in general, the median values would be the best parameter for characterizing radio source properties, since the cosmological interpretation of the distributions of these properties assumes that radio sources are randomly distributed in space. Thus, the plot of median value data in six redshift bins is superimposed on the plot in Figure 1. It can be deduced from the median value data that, on average, the angular size decreases sharply with increasing redshift at low redshift but remains fairly constant at high redshift. This observation apparently deviates from the expectation of the standard model with any of the different values of Ω0 (e.g Okoye and Onuora, 1982). This deviation can be explained using pure linear size evolution (Okoye and Onuora, 1982), luminosity selection/temporal evolution (Ubachukwu, 1995) and radio source orientation (Onuora, 1991).
3. Pure linear size evolution
Linear sizes of EGRSs have been found to evolve with cosmological epoch (Miley, 1968; Gall et al., 2011). Many authors (e.g Onuora and Okoye, 1983) suggested that linear size evolution can possibly interpret the deviation of θ − z data from the standard Friedmann world models. The variation of the linear size of extragalactic radio sources with redshift can be expressed (e.g Kapahi, 1975) as,
where D0 is the intrinsic linear size and depends on the assumed cosmology. To investigate the D − z data of the sample in the context of the inflationary universe, the scatter plot of D as a function of z is shown in Figure 2. The plot of median value data in six redshift bins is superimposed on the figure. It can be deduced from the median value data in Figure 2 that on average, the linear size increases with increasing redshift up to a value logDc = 2.5kpc (Dc = 316.23kpc) at zc = 1, after which it decreases with increasing redshift. This can be interpreted to mean that the present data is consistent with the inflationary model of the universe (Ω0 = 1). The regression analyses yield: logD=2.37kpc+0.003logP(WHz−1), with r = 0.04, and log D = 2.67 kpc −1.59 log P (WHz−1), withr≈−0.6forz<1andz≥1respectively. The median values give a stronger trend with correlation coefficients of +0.95 and −0.90 for z < 1 and z ≥ 1 respectively. The regression analyses for the D − z data yield: log D = 2.55 kpc + 0.09 log (1 + z), with r ≈ 0.12 and logD = −1.59kpc +2.67log(1 + z) with r ≈ −0.5, for z < 1 and z ≥ 1 respectively. Using Equation (4) in (1) yields,
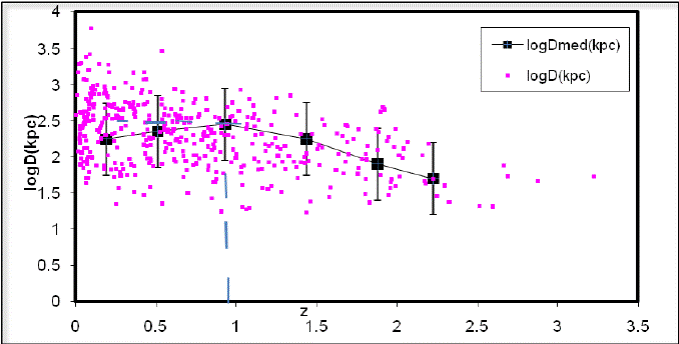
Fig. 2 Scatter plot of logD (kpc)) versus z for all sources (circles) with median values (filled squares) superimposed.
Equation (5) thus can be used to interpret the effect of linear size evolution in the θ − z relation for any radio source, where k is the amount of linear size evolution required to provide a good fit to the observed θ − z data for an assumed value of Ω0. It has bee shown that for any assumed value of Ω, 1 ≤ k ≤ 2, (Okoye and Onuora, 1982; Oort et al., 1987) is required to provide good fit to the observed θ − z data of EGRS samples.
The amount of linear size evolution needed to interpret the present θ−z data in terms of the standard cosmological model can be determined using Ω0 = 1, on the supposition of inflationary universe (e.g Peebles, 1988), superimposed on the observed θ−z plot, and allowing for linear size evolution (cf Equation 5) as shown in Figure 3. It is seen that a fairly good fit to the data can be obtained for k = 1.0, shown with the dotted curve in Figure 3. Hence, for an inflationary universe, the observed θ − z data of EGRSs can also be explained in terms of the standard cosmological model by linear size evolution; this suggests that radio galaxy and quasars are derived from the same parent population of radio sources and can be unified using the same amount of linear size evolution with k = 1.0.
4. Luminosity selection effect and temporal evolution
The variation of θ − z relation from any standard model can also be explained by invoking the luminosity selection effect (Ubachukwu, 1995) and a temporal evolution frame work (Masson, 1980). Hence, it follows that luminosity selection effect and temporal evolution are inherent in the size evolution of extragalactic radio sources. The linear size - luminosity (D − P ) relation can be expressed as a general power law of the form (e.g Masson, 1980; Aird et al., 2010)
where D0 is a constant and q is the slope representing the temporal evolution parameter. To model the temporal evolution of the sample, the projected linear size (D) is plotted against the radio luminosity (P) in Figure 4. Similarly, the median value data in nine uniform luminosity bins are superimposed on the plot.
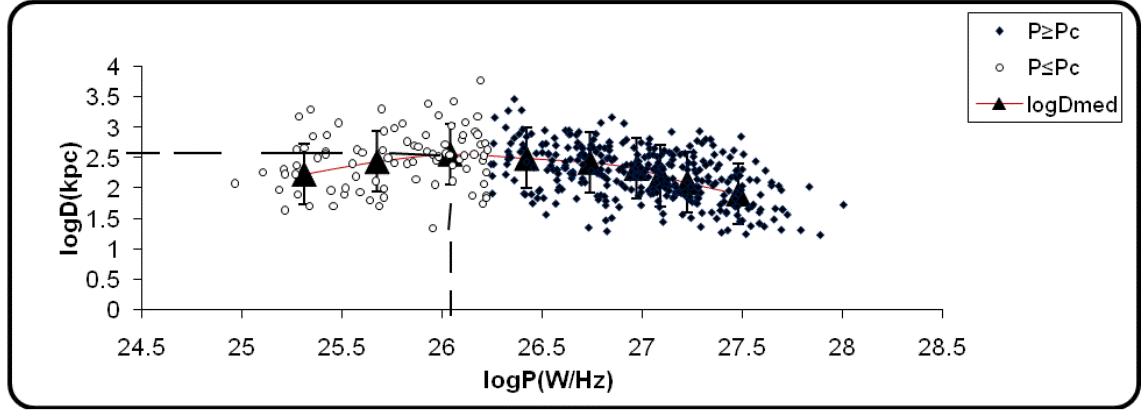
Fig. 4 Scatterplot of log D (kpc) versus log P (WHz−1) for both sources with P < Pcrit (open circle), P ≥ Pcrit (filled square) and median (filled triangle) values superimposed.
There is a general trend by which the linear size first increases with increasing luminosity up to a certain value and thereafter decreases. This trend is quite obvious in the median value data. The median value data suggest that the turnover occurs at critical point of luminosity, log Pcrit = 26.33 WHz−1 and log Dc = 2.51 kpc (316.23 kpc). The regression analyses yield: log D = 4.91 kpc + 0.29 log P (WHz−1), with r ≈ 0.21 and logD = 6.48kpc − 0.53logP (WHz−1) with r ≈ −0.7 for P < Pcrit and P ≥ Pcrit respectively. The regression analyses for the corresponding D − z yield: logD = 2.51kpc 0.81log(1+z); r ≈ −0.05 and logD = 2.63kpc 1.50 log(1+z); r ≈ −0.6 for P < Pcrit and P ≥ Pcrit respectively. A summary of the results of the regression analysis of the D−P, D−z and P −z data for sources withP <Pcrit andP ≥Pcrit ,z<1andz≥1is presented in Table 1.
Table 1 Results of the D P/Z and P Z regression analyses
| Parameters | D - P | D - z | P-z | ||||||
|---|---|---|---|---|---|---|---|---|---|
| D0 | q | r | D0 | k | r | P0 | β | r | |
| P< Pcrit | 4.91 | +0.29 | 0.21 | 2.51 | −0.81 | −0.05 | 25.55 | 5.64 | 0.5 |
| P≥ Pcrit | 6.48 | −0.53 | −0.7 | 2.63 | −1.50 | −0.6 | 26.42 | 2.20 | 0.8 |
| z < 1 | 2.37 | 0.003 | 0.04 | 2.55 | 0.09 | 0.12 | 25.63 | 7.58 | 0.5 |
| z ≥ 1 | 2.67 | −1.59 | −0.60 | 2.67 | −1.59 | −0.50 | 27.40 | 2.10 | 0.6 |
For a more homogenous source sample, the linear sizes of extragalactic radio sources have been suggested to separately depend on redshift and luminosity according to equations (4) and (6) respectively.
However, there is a tight dependence of luminosity on redshift due to Malquist bias, as:
The P −z plot of the sample is shown in Figure 5. It can be observed that the plot shows a steep change in the P −z slope at log Pcrit = 26.33 WHz−1 around z ≈ 0.3. This Pcrit is the value of P in Figure 4 that corresponds to Dc at zc ≈ 1. The fact that the Pcrit value is consistent with zc ≈ 1 suggests that P − z of the present sample is obtained by assuming Ω0 = 1, on the supposition of an inflationary universe. In effect, luminosity - dependent linear size evolution is envisaged. In the light of the above, the evolution parameter, k is therefore expected to be a function of both linear size evolution and luminosity selection effects. Hence, the linear size evolution of extragalactic radio sources can be written as a function of both redshift and luminosity in a general form (Kapahi, 1989; Ubachukwu, 1995) as
where m is a parameter that measures the residual cosmological evolution when the effect of luminosity is eliminated.
The observed D − z relation can be expressed in the form of Equation (4) if the correlation is entirely a result of luminosity selection effect in any source sample, but if there is residual linear size evolution (m) independent of the luminosity effect, it could unambiguously be expressed (e.g. Ubachukwu and Ogwo, 1998) as:
Equation (9) gives the residual luminosity effect independent of cosmological evolution for any source sample in which the luminosity effect dominates the linear size evolution (e.g Ubachukwu, 1995). Therefore, Equation (9) suggests that the value of the product qβ determines the amount of contributions to the size evolution resulting from luminosity selection and temporal evolution effects. The value and nature of the product is fundamental in investigations of the nature and amount of linear size evolution present in radio source populations.
For a sample with high flux density limit, 1≤k≤2 would be required to interpret the θ−z data (Okoye and Onuora, 1982). Alternatively, values of β appear to be similar for radio galaxies (irrespective of flux density limits) and quasars. Onuora and Okoye (1983) found 3.7 ≤ β ≤ 4.4 for the two bright samples they considered, depending on the value of Ω0. Also, Ubachukwu et al. (1993) found β ≈ 4.6 for the Kron et al. (1985) radio galaxies (S1.4 ≥ 0.6mJy). The value of q, on the other hand, appears to differ remarkably for radio galaxies and quasars. In fact, it has been noted that q ≈ 0.3 was obtained for radio galaxies that are mostly located at low redshift (Kapahi, 1987), while for radio quasars located at relatively high redshift, q ≈ −0.64 (Barthel and Miley, 1988). Ubachukwu, (1995) noted that q ≈ −0.5 for quasars from 30 extended quasars in the 3CR sources sample. In the present analysis, for all radio sources at P < P where radio galaxies are predominant, q ≈ 0.29, while for sources located at P > Pcrit where quasars dominate, q ≈ −0.53. This implies different values of q for radio galaxies and quasars. It should therefore be expected that the nature and amount of residual size evolution needed to interpret the θ − z data, independent of luminosity, should differ for radio galaxies and quasars. Hence, assuming k = 1.0 (e.g Okoye and Onuora, 1982) and β = 4.2 (Onuora and Okoye, 1983) for radio galaxies and quasars, we find q = 0.3 for radio galaxies and −0.5 for quasars. Consequently, we find different values of m for the two classes of objects (cf Equation 9), namely m = −0.26 for radio galaxies and m = 3.1 for quasars.
Therefore, if D and P evolve as earlier predicted, putting Equation (7) into Equation (6) yields:
so that using equation (10) in (1) yields,
where P±q/2c is the normalized angular size, and α = 2qβ is a parameter measuring the nature and amount of temporal evolution and luminosity selection effects without any significant linear size evolution.
To determine the amount of temporal evolution needed to explain the present θ − z data in terms of the standard cosmological model, the standard model with Ω0 = 1 is superimposed on the observed θ − z plots and, allowing for temporal evolution, q = 0.3 for radio galaxies and q = −0.5 for quasars, (cf Equation 11) as shown in Figure 6a and Figure 6b for radio galaxies and quasars respectively.
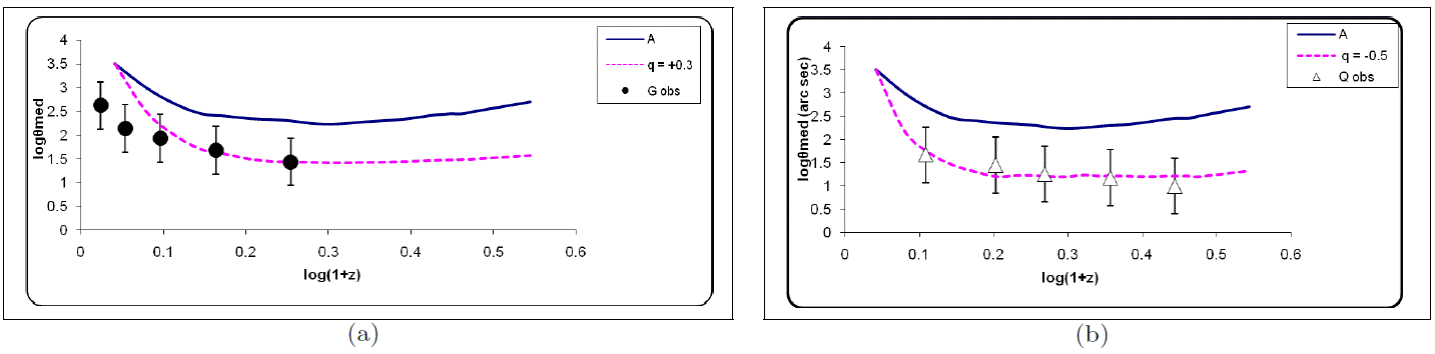
Fig. 6 (a) logθmed − log(1+z) plot for the present sample with standard cosmological model (curve A) and world model allowing for temporal evolution, q = +0.3 for radio galaxies.
It could be seen that fairly good fits to the data can be obtained for q = 0.3 and −0.5, shown with the dotted line in Figure 6a and 6b respectively for radio galaxies and quasars. Thus, the observed θ − z data of EGRS can be explained in terms of the standard cosmological model by temporal evolution independent of a linear size evolution effect, which implies that radio galaxy and quasars are essentially derived from the same parent population, which evolves with the same amount of temporal evolution.
5. Radio source orientation
Radio source orientation can also be invoked to interpret the observed θ−z departure from the standard Friedmann model (Onuora, 1991). Hence, if we assume a random radio source orientation, the linear size of all radio sources lying at small angles to the line of sight would appear foreshortened due to projected effects in the form:
where D0 is the intrinsic linear size and φ is the orientation angle. Thus, putting this Equation (12) into (1) gives (e.g Ubachukwu & Onuora, 1993).
Hence, for any world model, Equation (13) can generally be expressed (e.g Ubachukwu & Onuora 1993) as:
where Az is a factor which depends on the assumed cosmology and θ0 = D0 H0 Ω2/2c is the normalized angular size. Equation (14) gives the θ − z relation for a radio source for which the orientation effect has been admitted.
The observed median angular sizes as a function of (1 + z) for the present sample, in six comparable redshift bins are plotted in Figure 7. Assuming the projection angles (φ) of 59° and 33° for radio galaxies and quasars respectively (Onah, 2014), which enabled the theoretical θ−z relation to be de-projected, both the standard Friedmann model (curve A) and the de-projected model normalized at z = 0.1, where evolutionary effects are expected to be negligible, are superimposed on the θ−z plot as shown in Figures 7a and 7b. Obviously for Ω0 = 1, the observed θ − z data of the present sample are fairly fitted by the de-projected (doted curve) model.
6. Discussion
In this paper, we investigated the effects of cosmological linear size evolution, luminosity selection effects, temporal evolution frame work, and radio source orientation paradigm to explain the departure of the angular size - redshift (θ − z) relation of the present sample of EGRSs from the standard model. We fitted the observed θ − z data with standard cosmological models based on a flat universe (Ω = 1), on the supposition of an inflationary world model (e.g Guth, 1981; Peebles, 1988).
Although the cosmological evolution of the linear sizes of radio sources appears to be fairly well established both theoretically (e.g Gopal-Krishna and Witta, 1987) and observationally (e.g Oort et al. 1987), whether there is in addition luminosity and/or space density evolution with cosmic epoch is yet to be constrained unambiguously from the observed data (Windhorst, 1984). Moreover, the amount of linear size evolution required to explain the observed θ−z data appears to depend on the flux density limit of the sample used as well as on the assumed value of the density parameter (Ω). Also, there appears to be a statistical difference in the radio size distributions of radio galaxies and quasars (e.g Singal, 1993). However, the distributions of these parameters can coarsely be accommodated in the unified schemes which posit that radio galaxies and quasars are derived from the same parent population of objects (Okoye and Onuora 1982). It has been shown (cf Figure 3) that the θ−z data of the present sample of radio galaxies and quasars can be fairly well understood in terms of the standard cosmological model and the unification scheme if a linear size evolution k = 1.0 is admitted.
Furthermore, luminosity selection effects and a temporal evolution frame work were used to interpret the θ−z departure from the standard model. In most analyses, the usual assumption is that the cosmological and temporal evolution parameters, k and q respectively, are the same everywhere in the P − z plane. On the contrary, Ubachukwu et al. (1993) together with Ubachukwu and Ogwo (1998) suggested that this assumption is true only above a certain redshift cut-off, zc = 0.3. However, even estimating the D − z relation over some residual luminosity/redshift range still leaves some residual luminosity effects in the analyses (e.g Barthel and Miley, 1988). Using equation (9), this luminosity effects on the D − z correlations are easily eliminated. The present results suggest that the observed D − z correlation in the sample studied could be largely attributed to luminosity selection and temporal evolution effects. It has been shown in the results that the D − z correlations in the present sample is clearly dominated by luminosity selection and temporal evolution effects. In fact, the product of luminosity selection and temporal evolution effects dominates the cosmological evolution such that the observed θ − z relation can be explained in terms of the product alone, without invoking a significant linear size evolution. Nevertheless, it has been shown (cf Figures 6a and 6b) that the observed θ − z data of the present sample can be fairly well understood in terms of the standard model if temporal evolution parameter with q = 0.3 for radio galaxies and q = −0.5 for quasars is admitted. Singal (1993) and Ubachukwu (1995) suggested that the observed θ − z data of a sample of radio quasars could be explained in terms of luminosity effects alone without any significant linear size evolution. The present results are therefore consistent with previous results. For the extended steep spectrum sources, it is believed that the product of luminosity selection and temporal evolution effects is very strong and accounts largely for the observed D − z correlations. Alternatively, it is shown in the results (cf Figure 7a and 7b) that any linear size evolution in the sample disappears when orientation effects are corrected for by de-projection (D ≈ sin φ). Hence, linear size evolution in the present sample also seems to be orientation dependent.
Generally, the linear size evolution of the present sample can be seen in the light of luminosity and orientation dependence, so that an orientation - luminosity - dependent linear size evolution of the form
would be required to fully interpret the observed θ−z data of EGRSs, with q=0.3,φ=59°,m=−0.26 for radio galaxies and q = −0.5, φ = 33°, m = 3.1 for radio quasars respectively. All the results were found to be consistent with the popular quasar/galaxy unification scheme. The unified scheme posits that these sources should all belong to the same parent population of radio sources, the only difference between them being a result of orientation, obscuration or evolution. Hence, the observed differences between radio galaxies and quasars could be a result of size evolution, temporal evolution and radio source orientation.











 nueva página del texto (beta)
nueva página del texto (beta)






