1. INTRODUCTION

The study of the chemical composition of H II regions is crucial for the understanding of the chemical composition of the universe; it can provide observational constraints required by models of galactic chemical evolution. The proper determination of the oxygen abundance in H II regions is critical to be able to compare our determinations with other branches of astrophysics, as well as to be able to present a coherent model of the evolution of the universe.

Although a comprehensive chemical composition is desired, frequently studies are only able to determine a few chemical elements; in fact many works focus only on the oxygen abundance. A single well determined element can be quite useful, since most elements are expected to behave in an orchestrated fashion, and oxygen is the ideal candidate, since it is expected to comprise about half of the heavy element abundance; not only that, but is the easiest element to study since it is the only element that produces bright optical lines for each of its main ionic species.

There are three competing methods to derive ionic O⁺ and O⁺⁺ abundances, relative to the H⁺ abundance, in H II regions: (i) The use of ENT#091;O IIENT#093; and ENT#091;O IIIENT#093; collisionally excited lines (CELs) together with the H Balmer lines; these lines are relatively easy to observe. Unfortunately their emmisivities depend strongly on the local temperature (in fact, this specific characteristic of CELs is used to determine the characteristic temperature of photoionized regions); this is known as the direct method (DM). (ii) The use of O I and O II recombination lines (RLs) together with the H Balmer lines (which are also RLs); this strategy has the advantage that the ratios of any pair of RLs are almost independent of the temperature structure; however, RLs of heavy elements are quite faint and harder to work with. (iii) The use of CELs with the t ² formalism introduced by ^{Peimbert (1967)}; ^{Peimbert & Costero (1969)} in which the effect of the temperature structure on the emission lines is taken into account. Recent reviews of these methods have been presented by ^{Pérez-Montero (2017)}; ^{Peimbert et al. (2017)}; ^{Peimbert (2019)}; ^{García-Rojas (2020)}.

Abundances derived from either RLs or the t ² formalism usually agree with each other and are usually 0.2 to 0.3 dex higher than those determined using the DM (e.g. ^{Esteban et al. 2009}; ^{Peimbert et al. 2017}; ^{Peimbert 2019}; ^{Carigi et al. 2019a}). We have defined the temperature independent method (TIM) as abundances derived from either RLs, the t ² formalism, or their average (^{Carigi et al. 2019a}). On the other hand, the ratio between RL abundances and DM abundances (TIM abundances to DM abundances) is called the abundance discrepancy factor ADF:ADFX+i=XRLs+i/XCELs+i (^{Tsamis et al. 2003)}.

Whether the origin of the abundance discrepancy is (only) due to temperature fluctuations (^{Peimbert 1967)} or to chemical inhomegeneities (first proposed by ^{Torres-Peimbert et al. 1990)} is still under discussion (see e.g., ^{Esteban, Toribio San Cipriano & García-Rojas 2018}; ^{García-Rojas et al. 2019}). Other hypotheses have not been very successful and have been proposed over the years, such as the κ distribution of electrons (^{Nicholls, Dopita & Sutherland 2012)}, or uncertainties in the atomic data (e.g., ^{Rodríguez & García-Rojas 2010}), but have been discarded (^{García-Rojas et al. 2019}). Anyway, it is beyond the scope of this paper to discuss the origin of this long-standing problem.

Oxygen observations of H II regions are limited to the O⁺ and O⁺⁺ gaseous components. In general, it is not necessary to correct for other ionization stages where O⁺³ is limited to ≈ 1-2% and O⁰ is considered to be outside the relevant volume of the H II region; and, when comparing abundances between several H II regions, this is enough. However, when comparing with other types of objects, or when trying to model the evolution of a galaxy, it is of critical importance to correct for oxygen atoms trapped in dust grains, which are estimated to be ≈ 25% of the total oxygen in H II regions (i.e. an additional ≈ 35%, when compared to the gaseous component; ^{Mesa Delgado et al. 2009}; ^{Peimbert & Peimbert 2010}; ^{Espíritu et al. 2017}).

Here we study the discrepancy between TIM and DM abundances from a different perspective. We will compute chemical evolution models adopting the initial mass function (IMF) by ^{Kroupa (2002)} with different M_up values, where M_up is the upper mass limit of the IMF. The M_up value is not the maximum stellar mass present in a given H II region, but the maximum mass of the IMF averaged over the age of the Galaxy.

In order to be able to study in depth as many details as possible, in this paper we will do a deeper study for a few of H II regions only. We selected the Orion Nebula because it is, by far, the most studied Galactic H II region. For our second object we selected M17 because it is the second most studied Galactic H II region, it is relatively close by, yet it has an appreciably different galactocentric distance; also it is a high-ionization H II region and thus we need not worry about the possible presence of neutral helium. Our last object is M8; it is one of the most studied Galactic H II regions, it has approximately the same galactocentric radius as M17.

Chemical evolution models for the MW have been built to reproduce robust observational constraints of the Galaxy. Some authors (e.g., ^{Prantzos et al. 2018}; ^{Romano et al. 2010}) constrain their CEMs by trying to fit the solar abundances at the Sun’s age; other authors (e.g., ^{Spitoni et al. 2019}; ^{Mollá et al. 2015}) constrain their models by trying to reproduce the ENT#091;α/FeENT#093; - ENT#091;Fe/HENT#093; trend shown by stars at the solar vicinity. Most of these models reproduce the current slope of the α/H gradients, but the predicted absolute values are different and, consequently, the predicted α enrichment efficiencies are different during the last few Gyrs of the evolution.

Unfortunately, the chemical gradients of H II regions cannot be used as solid constraints because, while the slope of the chemical gradient is widely accepted, the absolute values of H II region gradients found in the literature present a large dispersion; this becomes more pronounced when combined with gradients derived from other young objects.

To improve the quality of the models, it is important to fit the absolute value of the element abundances at the present time, not only the slope. These absolute values become critical to place restrictions on the CEMs. For example: since O, and other α elements, are mainly produced by massive stars, the absolute values of the gradient are critical to determine the M_up value of the IMF.

For simplicity we will use H, He, C, and O to represent the abundances by number, and X, Y , C, and O to represent the abundances by mass of these elements; Z represents the total heavy element abundance by mass.

2. H II REGIONS ABUNDANCES AND CHEMICAL EVOLUTION MODELS

2.1. O/H vs. Distance to the Galactic Center

In Figure 1 we present two sets of H II region data for O/H, one based on the TIM and the other based on the DM, as well as the best fit models to each data set. The observational data were compiled from ^{Esteban et al. (2004}, ²⁰¹³, ²⁰¹⁶, ²⁰¹⁷⁾; ^{Fernández-Martín et al. (2017)}; ^{García-Rojas et al. (2004)}; ^{García-Rojas et al. (2005}, ²⁰⁰⁶⁾; ^{García-Rojas et al. (2007)}; ^{García-Rojas, Simón-Díaz & Esteban (2014)}. The models, built to reproduce the O/H gradient, come from ^{Carigi et al. (2019a)}. For a more detailed description of the data selection, the model, and the fit see ^{Carigi et al.(2019a)}. All abundances have been corrected by the fraction of O trapped in dust grains (^{Peimbert & Peimbert 2010}; ^{Peña-Guerrero et al. 2012}; ^{Espíritu et al. 2017)}. The figure illustrates very well that the curves required to fit the TIM and the DM data are quite different; it is thus no surprise that the M_up required by the models to fit the TIM data and the DM data are very different: while the M_up used to fit the TIM data amounts to 80M⊙, the value used to fit the DM data amounts to 40M⊙.

When comparing these values with the ones observed for young objects (B-stars, Cepheids), we find that the model based on the TIM values produces an excellent fit between 5 and 17 kpc, while the model based on the DM values fails to reproduce the observations (^{Carigi, Peimbert, & Peimbert 2019b}).

Fig. 1 Values of O/H as a function of the distance to the galactic center. Models for t ² = 0.00 and for observed t ² values versus two chemical evolution models with different M_up values. The filled and dashed lines represent the radial distribution obtained with the TIM ( Mup=80M⊙) and DM Mup=40M⊙ models, respectively. The circles represent the values derived from observations: TIM values based on recombination lines (black), TIM values based on the calibration by ^{Peña-Guerrero et al. 2012} (empty), and DM values (grey). For further discussion, see ^{Carigi et al. (2019a)}. The color figure can be viewed online. 

2.2. Representation of the Chemical Evolution Models

We compute a set of nine chemical evolution models (CEMs) for MW like galaxies based on the work by ^{Carigi et al. (2019a)}; these models differ only in the adopted M_up value. We present the output of these models for 6.2 kpc, corresponding to the average galactocentric distance of M17 (6.1 kpc) and M8 (6.3 kpc), and for 8.34 kpc, corresponding to the galactocentric distance of the Orion Nebula.

The initial abundances of our models are: X(0) = 0.7549, Y (0) = 0.2451, C(0) = 0, and O(0) = 0, where Y (0) = 0.2451 ± 0.0026 is the primordial helium abundance derived by ^{Valerdi et al. (2019)}. Their Y (0) result is in good agreement with the value derived by ^{Planck Collaboration (2018)} that amounts to Y (0) = 0.24687 ± 0.00076.

We explore the M_up effects on the predicted value of Y , C, and O during the whole evolution. The galaxies are formed in an inside-out scenario of primordial infall, with the halo component formed from 0 to 1 Gyr and the disk component formed from 1 to 13 Gyr.

In Figures 2 and 3 we present the ∆O vs ∆Y evolution for R = 6.2 and 8.34 kpc, respectively. Moreover, in Figures 4 and 5 we show ∆O vs ∆C evolution curves computed for the same radii. The evolution curves are presented for nine CEMs that consider Mup=25,30,35,40,50,60,80,100,150 M⊙. For comparison, we present observational data for M17, M8, and Orion, using the DM and the TIM.

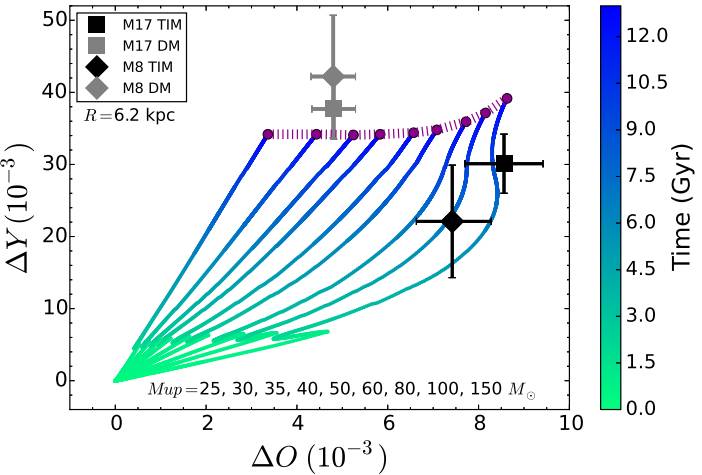
Fig. 2 Chemical evolution for Y and O at a galactocentric distance of 6.2 kpc (approximatelly the distance of M17 and M8). The curves cover the entire evolution from the beginning (0 Gyr) to the present time (13 Gyr, magenta points), and each curve corresponds to a model with a different M_up . The squares represent the O and He abundances derived for M17 using the DM (grey) and the TIM (black); the diamonds represent the abundances derived for M8 using the DM (grey) and the TIM (black). The dotted magenta line connects the present-time values predicted by the models. Note that, the observed values should be compared with this magenta line to choose the better M_up values. The color figure can be viewed online. 

Fig. 3 Chemical evolution for Y and O at a galactocentric distance of 8.34 kpc (Orion). The curves cover the entire evolution from the beginning (0 Gyr) to the present time (13 Gyr, magenta points), and each curve corresponds to a model with a different M_up . The circles represent the O and He abundances derived for Orion using the DM (grey) and the TIM (black). Note that the Orion data should be compared with the magenta line (theoretical present-time values). The color figure can be viewed online. 

Fig. 4 Chemical evolution for C and O at a galactocentric distance of 6.2 kpc (approximately the distance of M17 and M8). The curves and points are similar to those in Figure 2. Notice, however, that there are only 3 points in this figure instead of the 4 in Figure 2: unfortunately there is no restriction on C for the DM of M17 and, instead of the fourth point the shaded vertical band is the ∆O predicted by the DM. Again, the observed values should be compared with the magenta curve. The color figure can be viewed online. 

Fig. 5 Chemical evolution for C and O for a galactocentric distance of 8.34 kpc (Orion). The curves and points are similar to those in Figure 3. The Orion data should be compared with the magenta line. The color figure can be viewed online. 

In ^{Carigi et al. (2019a)}, models were built to reproduce the radial behavior of the total O/H from 21H II regions. To fit a representative absolute value of the gradient, they inferred two M_up values: one if the gaseous O/H values were determined from the DM (Mup=40 M⊙) and the other if the gaseous O/H values were determined from the TIM (Mup=80 M⊙), see Figure 1.

Also, for NGC 6822 (an irregular galaxy), ^{Hernández-Martínez et al. (2011)} built chemical evolution models to reproduce O/H values determined from DM and TIM, and obtained Mup=40 M⊙ and Mup=80 M⊙, respectively, in agreement with the values found for the MW.

In this work, we will obtain uncertainty bars for the M_up values, comparing the present-time abundances computed by models using different M_up values, with the O/H, He/H, and C/H abundances (and their error bars) for M17, M8, and Orion.

3. THE CHEMISTRY HAS A BETTER MEMORY THAN THE LIGHT

The lifetime of massive stars (few Myr) is very short compared to the age of galaxies (several Gyr); consequently, massive stars are not an important component of the light of the majority of the observed galaxies; yet, when massive stars die, their contributions are quickly incorporated into the chemistry of the ISM.

The chemical composition of an H II region is the result of the whole history of the chemical evolution of any given galaxy; therefore the chemical composition of H II regions can be compared with estimates of the present day chemistry derived from galactic CEMs; and we can infer the amount of formed massive stars (equivalently, the M_up value), comparing the chemical abundances in the ISM with those obtained from CEMs.

To study the most massive stars in the MW by looking for them at present has several major inconveniences: there are very few of these stars, this is compounded by the fact that they must be formed in very massive giant molecular clouds (GMCs), and they are the first ones to evolve (first shedding mass in strong stellar winds, and then going supernova, all this before the GMC is dissipated by the combined effect of the stars that are evolving inside it). Thus, they are usually obscured and very difficult to observe during their short lifespan. Moreover, most massive stars that can be observed today may not be representative of the most massive stars that have existed during the evolution of the Galaxy, i.e. the stars that have contributed to the evolution of the chemistry of the present day ISM as well as the chemistry available during the most recent star formation.

Based on the ∆Y comparison, between the observed values (from TIM or DM) and the preset-time predicted values (from CEMs), we cannot exclude any M_up value in the 25 - 150 M⊙range. However, from the ΔO comparison, we find agreement for Mup values in the 30<Mup<50 M⊙range for the DM, and in the 75<Mup<120 M⊙range for the TIM. Moreover, from the ΔC comparison, we find agreement in the 55<Mup<95 M⊙range for the TIM, and a suggestion of a very small Mup for the DM (Mup<25 M⊙). Therefore, by comparing TIM with CEMs, the best Mup values are in the 70≲Mup≲100 M⊙range; and by comparing DM with CEMs, the best Mup values are in the 25≲Mup≲45 M⊙ range.

^{Weidner et al. (2013)} in their Figure 3 showed the dependence of the star formation rate (SFR) on the integrated galactic stellar initial mass function (IGIMF, called IMF in our CEMs) for different power-law indexes, α, (for initial stellar masses between 1.3 M and M_up ). They noted that IMF for a SFR ≈1 M⊙/yr corresponds to an α=2.6 and to an Mup≈ 100 M⊙; and that these values are in agreement with the MW (we use α=2.7 for our CEMs). On the other hand, the SFR required to obtain Mup≈40 M⊙is SFR≈10-2M⊙/yr (as well as an α ≈ 2.8).

Regarding the observational determinations of the SFR: (i) the MW, a spiral galaxy (Sbc) with total stellar mass ≈1011 M⊙, presents a galaxy-wide SFR ≈0.7-2.3 M⊙/yr (^{Robitaille & Whitney 2010}; ^{Chomiuk & Povich 2011}); (ii) NGC 300, a small spiral galaxy (Sd) with total stellar mass =1.9×109 M⊙, presents a galaxy-wide SFR =0.08-0.30 M⊙/yr, approximately an order of magnitude smaller than the SFR in the MW (e.g. ^{Kang et al. 2016}, and references therein).

Moreover, based on spatially-resolved spectroscopic properties of low-redshift star-forming galaxies, ^{Sánchez (2019)} showed in his Figure 7 a difference of approximately 1 order of magnitude between the SFR of Sbc galaxies with stellar mass ≈ 10¹¹ M (as the MW galaxy) and the SFR of Sd galaxies with stellar mass ≈2×109 M⊙ (as NGC 300).

Therefore, the M_up values we derive from the TIM are consistent with the SFR of the MW galaxy, while the M_up values derived from the DM are consistent with a galaxy with a mass and SFR similar to those of NGC 300, but not with the mass and SFR of the MW.

Moreover the abundances derived from the TIM are consistent with those derived from observation of other young objects in the MW (Cepheids, B stars), while the abundances derived from the DM are approximately 0.25 dex too small.

The chemical composition of a given H II region is the result of the evolution of the ISM throughout the history of our Galaxy. Therefore, the chemical abundances of an H II region do not depend on the IMF of the observed H II region. In particular the most massive star of a given H II region is not representative of the most massive stars of the galactic IMF.

4. CONCLUSIONS

We have computed nine chemical evolution models (CEM) of a MW like galaxy; the only difference among these models is the IMF, specifically its M _up value, that ranges between 25 and 150 M⊙. We compare the model predictions with the O/H, He/H, and C/H values derived for three Galactic H II regions: M17, M8, and Orion. We compute the abundances by two different methods: the DM (direct method) and the TIM (temperature independent method); these methods have always given different results. We selected these objects because they probably have the best O/H determinations, and because their galactocentric radii are different enough to be useful as independent constraints for the CEMs (6.2 and 8.34 kpc, respectively). The comparison between models and observations tells us which is the M_up that better fits each set of observations.

It is useful to remember that the chemistry has a better memory than the observed UV light. In other words: the chemistry will explore the average M_up over the lifespan of the MW, while any measurement of the UV radiation or of the most massive stars observed can only be a reflection of the present day M_up (and can potentially have significant biases toward lower masses).

When comparing the models with the DM abundances we find: for ∆O, a 30<Mup<50 M⊙range; for ΔC, Mup<25 M⊙, while Y does not provide a significant restriction. Overall, the DM produces preferred values in the 25<Mup<45 M⊙range. On the other hand, when using the TIM abundances we find: for ΔO, a 52<Mup<150M⊙range; for ΔC, a 25<Mup<95 M⊙range, while Y suggests a smaller value, but does not provide a significant restriction. Overall the TIM produces preferred values in the 70<Mup<100 M⊙range.

Moreover the M_up in a given galaxy is directly related to the SFR, and the SFR is directly related to the mass of any given galaxy. A MW like galaxy, with a SFR ≈1 M⊙/yr, is expected to have an Mup≈100 M⊙, in good agreement with the TIM determination, but not with the DM determination (which would be more consistent with an Sd galaxy with a SFR ≈0.01 M⊙/yr).