1. Introduction and Motivation
A major challenge in gravity and modern cosmology is the late-time cosmic acceleration (Perlmutter et al. 1999, Percival et al. 2001, Stern et al. 2010). The existence of ’Dark Energy’ (DE) with negative pressure which represents a repulsive gravity is one possible explanation. A variety of DE models have been suggested through modified gravity theories (Tsujikawa 2013, Kamenshchik et al. 2001, Caldwell 2002, Chiba 2000, Sen 2002, Arkani-Hamed et al. 2004, Ahmed 2018) and dynamical scalar fields (Harko et al. 2011, Nojiri et al. 2017, Nojiri and Odintsov 2006, Nojiri et al. 2008, Ferraro and Fiorini 2007, Bengochea and Ferraro 2009, De Felice and Tsujikawa 2010, Alves et al. 2011, Maeder 2017, Gagnon et al. 2011, Ahmed and Moss 2008, Ahmed and Moss 2010). Gravity also has a deep connection with thermodynamics; this connection has been proved through the entropy-area formula S = A/4G where S is the black hole’s entropy and A is its horizon area (Hawking 1975). The FRW cosmological equations can also be derived from the first law of thermodynamics (Cai and Kim 2005, Bousso 1999, Nojiri and Odintsov 2006). When higher order curvature terms appear, the entropy-area formula, which holds only for GR, needs corrections. Modified FRW equations have been given in Cai and Cao (2008) using the corrected entropy-area relation
The values of the two dimensionless constants α and β are in debate and not yet determined (Salehi and Fard 2018, Jing and Yan 2002). While positive and negative values of α and β have been suggested by some authors, it has been argued in (Gour 2002, Hod 2004, Xia et al. 2013, Yang and Xu 2014, Medved 2005) that the ”best guess” might simply be zero. A detailed discussion for all possible values has been introduced in Ahmed and Alamri (2019, 2019a) based on cosmological and stability arguments.
In spite of its success, the standard Big Bang model suffers from a number of problems such as the flatness problem, the horizon problem and the initial singularity problem. Although some problems have been addressed in the inflationary scenario in which the universe undergoes an exponential expansion for a very short interval of time, the initial singularity problem still remained unanswered (Guth 1981, Starobinsky 1980). An alternative theory free from the initial singularity is the Big Bounce, in which the universe arises from a prior contracting phase. In other words, the universe initially contracts to a minimal size before it starts to expand again (Novello and Bergliaffa 2008, Ijjas and Steinhardt 2018, Sahoo et al. 2020, Nojiri et al. 2019) (see Brandenberger and Peter, 2017 for a review of earlier bouncing scenarios). Such a contraction-expansion process may be repeated forever, which also gives the name cyclic cosmology to such models. Bouncing cosmology has been discussed in the framework of many modified gravity theories such as f (R) gravity, f (T) gravity, f (G) gravity, f (R, T), gravity (Bamba, et al. 2014, Bamba, et al. 2014, Bamba, et al. 2015, Bamba, et al. 2016, Tripathyet al. 2019) and teleparallel gravity (de la Cruz-Dombriz, et al., 2018).
While many bouncing models have been introduced, a special attention has been paid to the Matter Bounce Scenario (MBS)(de Haro and Cai 2015, Cai et al., 2013, Quintin et al., 2014, de Haro 2012, Wilson-Ewing 2013) which leads to a nearly scale invariant power spectrum of primordial curvature perturbations. In this scenario, the universe is nearly matter-dominated at very early times in the contracting phase and gradually evolves towards a bounce. At the bounce, all parts of the universe are supposed to be in causal contact which means no horizon problem (Nojiri et al., 2019). After that, a regular expansion starts in agreement with the behavior of the standard Big Bang model. Some unclear conceptual issues of the Matter Bounce Scenario have been discussed in detail in Nojiri et al. (2019). Although there has been a wide observational and theoretical support for the flat universe (Tegmark et al. 2004, Bennett et al. 2003, Spergel et al. 2003a, Ahmed et al. 2020), some other recent observations of cosmic microwave background anisotropies also suggest that our universe may be closed rather than flat (Di Valentino et al. 2020, Handley 2021, Planck Collaboration et al. 2020a, 2020b). The present theoretical work supports positive curvature; we show that the existence of a stable entropy-corrected bouncing cosmology implies a closed universe.
The paper is organized as follows: In § 2, a matter-bounce solution to the modified entropy-corrected cosmological equations is provided with the expressions for the pressure p, energy density ρ, EoS parameter ω, deceleration and the jerk parameters j and q. A complete analysis for the evolution of these functions with cosmic time is studied for different values of α and β for the three values of the curvature κ (= +1, 0, −1). § 3 is dedicated to the study of the stability of the model and § 4 to cosmography. The final conclusion is included in § 5.
2. Cosmological Equations and Solutions
Taking (1) into account, the following FRW equations can be obtained (Cai et al., 2008)
A general FRW model has been constructed in (Ahmed and Alamri, 2019a) where equations (2) and (3) have been solved using the hyperbolic ansatz a(t) =
the Matter Bounce Scenario can be explored via this ansatz when n = 1/3. The expressions for deceleration and Hubble parameters q and H can now be written as
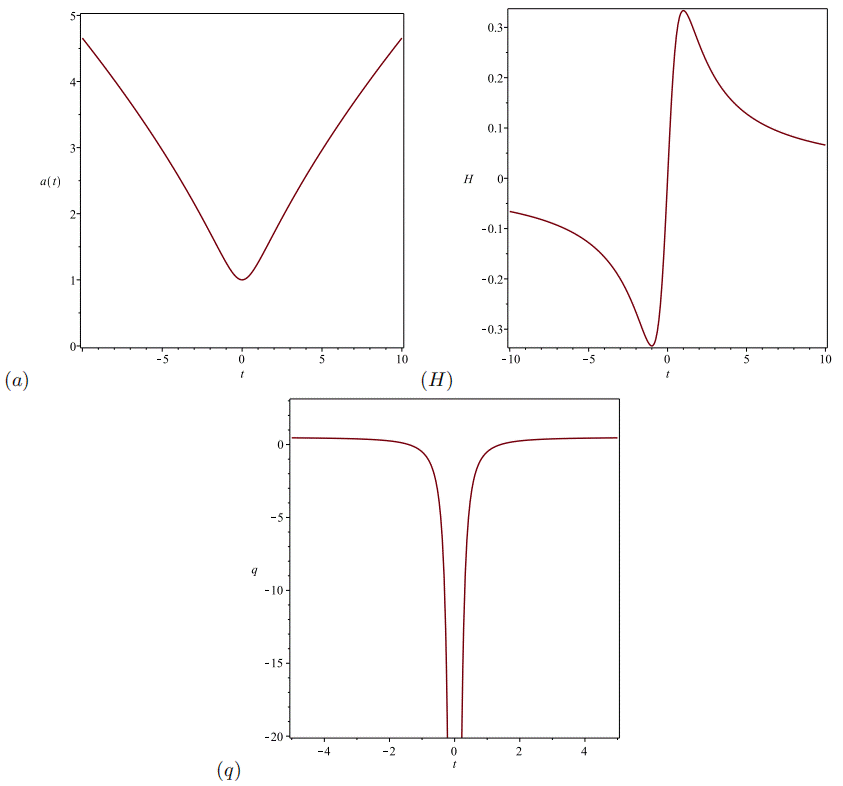
Fig. 1 The scale factor, Hubble and deceleration parameters for the MBS (n = 1/3). The Hubble parameter is negative before the bounce, positive after the bounce and zero at the bounce. The color figure can be viewed online.
The formulas for the pressure p(t) and energy density ρ(t) are
Figure 2 shows the evolution of the energy density, the pressure and the equation of state parameter with cosmic time. The evolution of ρ(t) shows that the only case allowed physically is the one with positive curvature k = +1. The plots of p(t) and ω(t) shows a Quintessence-dominated universe along with negative pressure. The existence of negative pressure agrees with the ’dark energy assumption’ which implies a negative pressure. Such evolutions of the three parameters have been found to be independent of the values of the prefactors α and β as shown in Table (2). The jerk parameter has the asymptotic value j = 1 at late-time. After making use of the relation between the scale factor and the redshift a = 1/1+z to express ω in terms of z, we find that
ω(z) = −1 at the current epoch where z = 0.
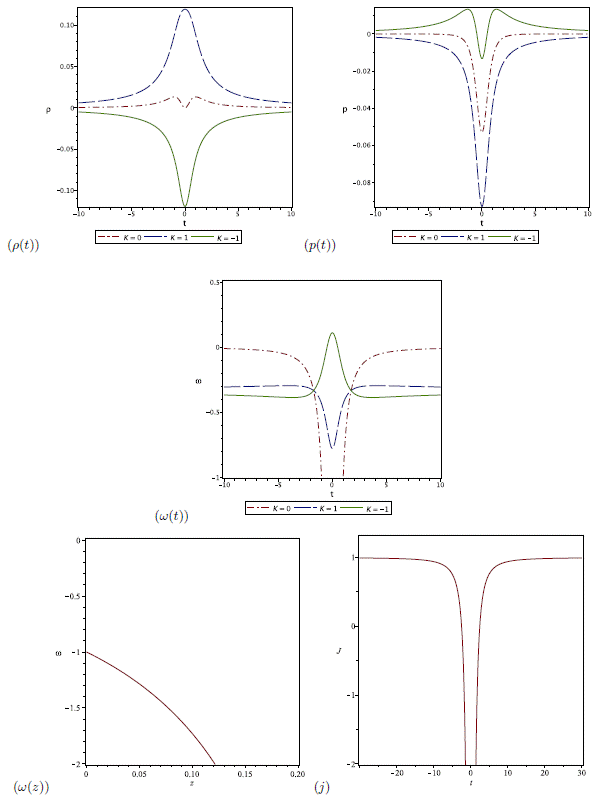
Fig. 2 Evolution of ρ, p and ω for the matter bounce scenario (n = 1/3). (a) The physically accepted behavior of energy density exists only for a closed universe. (b) The pressure is always negative. (c) The equation of state parameter for a closed universe lies in the range −1 < ω < 0 which means a Quintessence-dominated universe. The same behavior of ρ, p and ω has been obtained for different values of α and β (Table 1). (d) Equation of state parameter ω as a function of the redshift z; we see that ω(z) = −1 at z = 0. (e) The jerk parameter has the asymptotic value j = 1 at late-time. Here A = 1.5. The color figure can be viewed online.
Table 1 In the Current Bouncing Model, Evolutions of ρ, P and ω Are Independent of The Values Of α And β
| α | 0.1 | 0 | 0.2 | -0.1 | 0 | -0.5 | 0 | 0.01 | 0 |
| β | 0.1 | 0.3 | 0 | -0.1 | -0.7 | 0 | 0.02 | -0.001 | 0 |
| Same behavior of ρ(t) ? | ! | ! | ! | ! | ! | ! | ! | ! | ! |
| for all | for all | for all | for all | for all | for all | for all | for all | for all | |
| k | k | k | k | k | k | k | k | k | |
| Same behavior of ρ(t) ? | ! | ! | ! | ! | ! | ! | ! | ! | ! |
| for all | for all | for all | for all | for all | for all | for all | for all | for all | |
| k | k | k | k | k | k | k | k | k | |
| Same behavior of ρ(t) ? | ! | ! | ! | ! | ! | ! | ! | ! | ! |
| for all | for all | for all | for all | for all | for all | for all | for all | for all | |
| k | k | k | k | k | k | k | k | k |
3. Stability of the Model
In this section, we discuss the validity of the classical linear energy conditions (Hawking and Ellis 1973, Wald 1984) and the new nonlinear energy conditions (ECs) (Martin-Moruno and Visser 2013, Abreu et al. 2011, Martin-Moruno and Visser 2013a, Martin-Moruno and Visser 2013b). The classical linear ECs (the null ρ + p ≥ 0; weak ρ ≥ 0, ρ + p ≥ 0; strong ρ + 3p ≥ 0 and dominant ρ ≥ |p| energy conditions) should be replaced by other nonlinear ECs when semiclassical quantum effects are taken into account (Martin-Moruno and Visser 2013a, Martin-Moruno and Visser 2013b). In the current work, we consider the following nonlinear ECs: (i) The flux EC (FEC): ρ2 ≥ p2 (Aberu et al. 2011, Martin-Moruno and Visser 2013), first presented in Aberu et al. (2011). (ii) The determinant EC (DETEC): ρ.Πpi ≥ 0 (Martin-Moruno and Visser 2013b). (ii) The race-of-square EC (TOSEC): ρ2 + Σρi2 ≥ 0 (Martin-Moruno and Visser 2013).
According to the strong energy condition (SEC), gravity should always be attractive. But this ‘highly restrictive’ condition fails when describing the current cosmic accelerated epoch and during inflation (Visser 1997a, Visser 1997b, Visser 1997c). In the current model we have a negative pressure which represents a repulsive gravity and, consequently, the SEC is not expected to be satisfied as indicated in Figure 3b. Only for the closed universe (K = +1), the null energy condition (NEC) (Figure 3a) and the dominant energy condition (Figure 3c) are satisfied all the time. Although most models of non-singular cosmologies require a violation of the NEC (ρ + p ≥ 0), avoiding such a violation would be preferable, if possible. The NEC is the most fundamental of the ECs and on which many key results are based, such as the singularity theorems (Alexandre and Polonyi 2021). Violation of NEC automatically implies the violation of all other point-wise energy conditions.
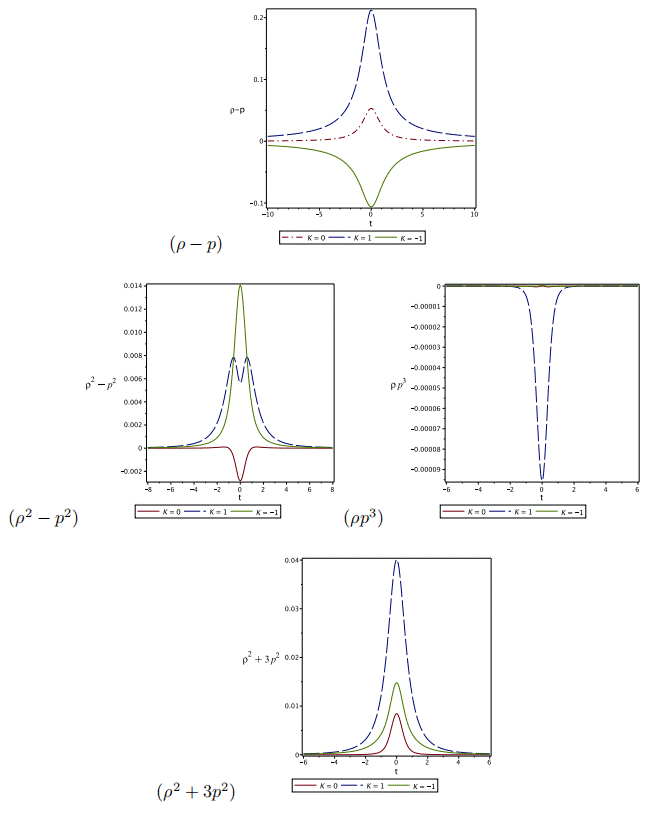
Fig. 3 Classical and nonlinear ECs: No violations of NEC and DEC for k = +1. The color figure can be viewed online.
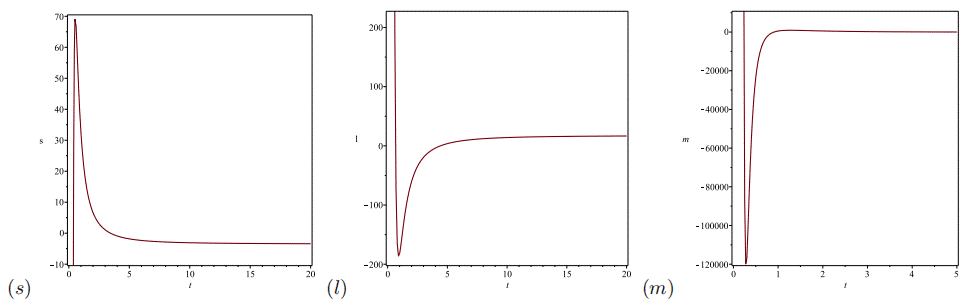
Fig. 4 Evolution of the cosmographic parameters s, l and m with time. The color figure can be viewed online.
A classical non-singular bouncing cosmological model in which the NEC is not violated was introduced in Gungor and Starkman (2021). A detailed discussion on the relation between the enforcement of the NEC and the occurrence of bouncing universes was given in Giovannini (2017). It has been shown in Bramberger and Jean-Luc Lehners (2019) that a combination of positive spatial curvature and vacuum energy (violating the SEC) leads to non-singular bounces with no violation of the NEC. Recalling the definition of Dark Energy as a component of negative pressure, our result in the current work agrees with the result obtained in Dunsby and O. Luongo (2016). We also obtain a combination of positive curvature, violation of the SEC, and a bouncing universe without violation of the NEC. A non-singular bouncing cosmological model with positive spatial curvature and flat scalar potential was constructed in Capozziello (2019). The behavior of the new nonlinear ECs is plotted in Figure 3d, e, f. For the closed universe, both the flux and trace-of-square ECs are satisfied.
4. Cosmographic Analysis
The cosmography of the universe has recently been an attractive area of research (Visser 2005, Capozziello et al. 2019) where cosmological parameters can be described in terms of kinematics only. Consequently, cosmographic analysis is model-independent with no need to assuming an equation of state in order to explore the cosmic dynamics (Visser, 2005). The Taylor expansion of the scale factor a(t) around the present time t 0 can be written as
The following cosmographic coefficients of the series (8) are recognized respectively as the Hubble parameter H, the deceleration parameter q, the jerk j, the snap s, the lerk l and the max-out m parameters
For the current model, the expressions for H and q have been given in (5). The expressions for j, s, l and m are given as
The sign of q determines whether the expansion is accelerating (negative sign) or decelerating (positive sign). j represents a suitable way to describe models close to ΛCDM (Visser, 2005). The sign of j is also important; the positive sign shows the existence of a transition time when cosmic expansion gets modified; the value of s is necessary to determine the dark energy evolution. In spite of its advantages, a useful discussion on the limits and drawbacks of the cosmographic approach has been given in Visser (2005).
5. Conclusion
In this paper, we have constructed a matter bouncing entropy-corrected model using a special ansatz for a variant non-singular bounce (Nojiri et al., 2019). The main features of the present model are as follows:
Only a closed universe is allowed in the model. While the strong energy condition is violated, the null and dominant energy conditions are satisfied all the time only for K = +1. Although most models of non-singular cosmologies require a violation of the NEC, it is highly preferable to avoid such violation if possible. The new nonlinear energy conditions has also been investigated.
The evolution of the equation of state parameter and of the cosmic pressure shows a Quintessence- dominated universe along with negative pressure. In the current model we get ω(z) = 1 at the present epoch where z = 0, as it should be according to observations.
The result obtained in the current work agrees with the result obtained in Bramberger and Jean-Luc Lehners (2019), where the combination of positive spatial curvature and vacuum energy (violating the strong energy condition) leads to non-singular bounces with no violation of the null energy condition. Our result also agrees with the works of Giovannini (2017), Matsui et al. (2019). This represents a strong support for the current work, where similar results have been obtained in different work frames.
We have examined many positive, negative and zero values for α and β and found no change in the behavior of the cosmic pressure, energy density and equation of state parameter. This is another interesting feature of this entropy-corrected bouncing model, where the evolutions of p, ρ and ω are independent of the constants α and β.
The cosmographic parameters have been analyzed.











 nueva página del texto (beta)
nueva página del texto (beta)


