Introducción
Para las compañías de seguros, gobiernos y entidades públicas y privadas que tienen a su cargo el pago de pensiones de vejez, vida o invalidez, el cálculo de la reserva actuarial necesaria para cubrir la totalidad de los pagos de una renta vitalicia es un tema fundamental. Existen trabajos que muestran que, en los países latinoamericanos, no es suficiente la pensión obtenida por los trabajadores al momento de su jubilación, como son los desarrollados por Gómez & Kato (2008), dónde analizan qué tan competitivas son las pensiones en México comparadas con las que se otorgan en otros países de América Latina, y sus resultados muestran que las comisiones cobradas son más altas en México que en Argentina y Chile, lo que implica que la pensión mensual que obtiene el trabajador al momento de jubilarse sea menor en México; por tanto menos competitiva, que en los otros países. Duque, Quintero, & Gómez (2013) analizan el régimen subsidiado pensional colombiano desde el punto de vista de la eficacia del principio de universalidad, determinan que dicho régimen no es una herramienta eficaz para que sus beneficiarios puedan acceder a una pensión y Villagómez (2014) muestra que en general los individuos no tienen el ahorro necesario para su retiro, se encuentren en países desarrollados o no, en particular en el caso mexicano.
Mientras que Martínez & Venegas (2014) analizan el riesgo de mercado de los fondos de inversión: Siefore básica 1 (SB1) y Siefore básica 2 (SB2), mediante un índice de rendimientos incluidos en modelos ARIMA-GARCH, muestran que los rendimientos obtenidos son insuficientes para compensar el riesgo adicional asumido por los fondos de pensiones de renta variable; así como Damián (2016) trabaja sobre los inicios del nuevo sistema de pensiones en México, muestra la reducción en los beneficios de los futuros pensionados, debido a dicha reforma y analiza la pobreza generada a la población en edad de retiro, con respecto a las pensiones, contributivas y no contributivas. Bernal (2016) analiza los factores que explican el gasto en pensiones y proyecta su evolución al año 2075 en cuatro países de América Latina: Chile, Perú, Colombia y México, encuentra que el gasto de pensiones con respecto al PIB está entre 1,8 y 6,4%, pero se incrementará el doble y cuatro veces más en 2075, principalmente por el envejecimiento de la población; y Castañón & Ferreira (2017) muestran resultados de la densidad de cotización considerando diferentes cohortes de trabajadores que cotizan a las Afores y concluyen que los montos de cotización de dichos trabajadores son bajos y son insuficientes para una pensión digna.
Para los gobiernos, la estimación del monto de la reserva actuarial necesaria para cubrir la totalidad de los pagos de una renta vitalicia afecta directamente la cobertura y la estabilidad de los sistemas de pensiones y, por tanto, la sostenibilidad fiscal de los países que otorgan o subsidian las rentas vitalicias de la población; un desequilibrio en dicho sistema, afecta la sostenibilidad de las entidades que tienen a su cargo obligaciones pensionales, con probables desestabilizaciones sistémicas en la economía Grinols & Turnovsky (1993), Schmedders (1998). En el caso mexicano Banda & Gómez (2009) analizan el desempeño de las Sociedades de Inversión Especializadas en Fondos para el Retiro en México (Siefores) mediante los índices de Sharpe, Treynor y Jensen; concluyen que existe escasa relación entre los rendimientos del mercado y los rendimientos de las Afores y se espera que el riesgo asociado a las Siefores 3, 4 y 5 aumente, así como los rendimientos de los trabajadores, que son muy bajos.
El cálculo actuarial plantea que la estimación de las reservas de dinero, necesarias para soportar el pago de una renta vitalicia, se efectúa sumando los valores actuales esperados de los pagos futuros Bowers et al. (1997). En este cálculo intervienen diversas variables, tales como la probabilidad de vivir del individuo, la inflación, la edad, el monto del pago futuro posible y la tasa de interés de descuento; esta estimación no incluye la estructura estocástica de los activos incluidos en el portafolio, ni del portafolio total en el cual está invertida la reserva actuarial, por lo que los análisis se enmarcan en un mundo determinista.
Antecedentes y objetivos
Las metodologías de administración de portafolios basadas en coberturas mediante derivados financieros han sido ampliamente tratadas en la literatura. Especialmente desde la publicación de los modelos de Black & Scholes (1973) y de Merton (1973), estas estrategias son comúnmente utilizadas en los mercados financieros tanto para acciones, como lo indican Jarrow & Turnbull (1999); así como para bonos y demás títulos de renta fija, Jarrow (2002). Estrategias de ese tipo también han sido aplicadas en el contexto de los mercados de commodities; por ejemplo, para el caso de la energía eléctrica, Nässäkkälä & Keppo (2005). En diversos artículos, se ha abordado el estudio de fenómenos financieros a través de la dinámica estocástica de los precios, algunos de los trabajos con este tipo de este enfoque son Merton (1973), Black & Scholes (1973), Vasicek (1977), Cox & Ross (1976), Cox et al. (1985a) y (1985b), Hull & White (1990) y (1993), Black et al. (1990) y Heath et al. (1992).
El presente trabajo tiene por objetivo desarrollar un modelo para estimar la reserva actuarial de una renta vitalicia a una vida, utilizando procesos estocásticos; se plantea a partir de una estrategia de cobertura dinámica asociada a un derivado financiero, en dónde, dicha cobertura garantiza un valor futuro de la reserva para cada desembolso mayor, o por lo menos igual al pago a realizar. En la Sección 3, se presenta el modelo y en la Sección 4 se analizan los resultados de su implementación al Fondo de Pensiones de las Entidades Territoriales de Colombia y a los Fondos para el retiro de los trabajadores afiliados al Instituto Mexicano del Seguro Social (IMSS) y al Instituto de Seguridad y Servicios Sociales de los Trabajadores del Estado (ISSSTE) en México. Finalmente, en la Sección 5, se exponen algunas conclusiones.
El método
El modelo propuesto en esta sección, parte de la estimación de la reserva actuarial necesaria para soportar el pago de una renta vitalicia y de la descomposición de la obligación del pagador en una opción call en posición larga y una opción put en posición corta para cada uno de los desembolsos futuros. Posteriormente, se presenta una ecuación para estimar el valor presente de los excedentes del pagador de la renta cuando el valor reservado excede el monto a pagar. Además, se presenta una estrategia de cobertura dinámica, que a través de una opción put sintética, que permite anular cualquier déficit en la reserva actuarial para cada pago, generando excedentes en la mayoría de los casos. Dichos excedentes son valorados mediante el modelo de Cox, Ingersoll & Ross (1985b) y son restados al cálculo inicial de la reserva necesaria, junto con los costos generados por la cobertura dinámica (o sumados si se trata de ingresos).
Reserva necesaria para una renta vitalicia calculada a una vida
Una Renta Vitalicia, es un pago periódico de una pensión, durante toda la vida del pensionado; su cálculo, depende de su esperanza de vida. En los siguientes apartados se determinan los elementos necesarios para calcular la cantidad de dinero necesaria para respaldar el pago de una renta vitalicia utilizando la cobertura dinámica propuesta.
Probabilidad de sobrevivir
Sea S(x) una función de sobrevivencia que indica la probabilidad de que la edad de muerte (X) de una persona en particular sea mayor a una edad x. Por lo tanto:
Se define t p x como la probabilidad que tiene una persona de edad x de no fallecer en los próximos t años y t q x como la probabilidad de fallecer en el mismo período. De acuerdo con esta definición se tiene que:
Estas probabilidades pueden ser calculadas a través de tablas de mortalidad, las cuales son modelos de sobrevivencia presentados en forma tabular e ilustran el número de sobrevivientes de un grupo inicial, denotado como l 0, desde una edad particular x hasta la edad límite w⋅ l 0 es la raíz de la tabla o grupo inicial y l x es la cantidad estimada de sobrevivientes para la edad x. La relación entre la constante l 0 y la variable l x está determinada por la siguiente ecuación:
como,
por lo tanto,
Cálculo de la reserva actuarial
La reserva necesaria para el pago de una renta vitalicia es la suma de los valores presentes esperados de los pagos posibles Bowers et al, (1997). Se supone una renta vitalicia con una indemnización que aumenta en el mismo porcentaje que el nivel general de precios y que inicialmente corresponde a un valor D 0 en caso de no fallecer y de cero (0) en caso de fallecer.
donde:
|
Monto de la mesada en un instante t. |
|
Tasa de interés nominal. |
|
Edad actual del asegurado. |
|
Tiempo máximo que el asegurado puede vivir. |
|
Reserva necesaria para el pago de una renta vitalicia. |
Entonces,
En tiempo continuo puede expresarse de la siguiente forma:
Combinación de opciones como representación del pago de una renta
Sea V t el valor del fondo necesario para soportar el pago futuro D T , que se ejecuta siempre y cuando la persona de edad x sobreviva por lo menos T-t años más. Por lo tanto, el valor de dicho fondo corresponde al valor presente actuarial:
donde r es la tasa de interés técnico nominal utilizada para el cálculo actuarial y (T-t) p x es la probabilidad de que una persona de edad x sobreviva por lo menos T-t años más. Se supone que V t es conducido por la siguiente Ecuación Diferencial Estocástica (EDE):
Si V T < D T , se incumpliría con el pago o se tomaría dinero de la reserva para otro pago, desfinanciando así la reserva total. Además, no habría ningún tipo de excedente, que se denota como S T , en el portafolio que respalda la renta vitalicia; es decir, S T =0. Por otra parte, si V T ≥ D T se cumple con el pago y por lo tanto el excedente sería S T = V T - D T . En consecuencia, se sigue que:
Esto corresponde al pago en la fecha de vencimiento T de una opción de compra (call). Con base en las ecuaciones de Black & Scholes (1973) y Merton (1973), y suponiendo que la reserva para la renta vitalicia tiene una rentabilidad, denotada por r, igual a la tasa libre de riesgo, se tiene que:
donde:
y
A partir de
Si V t > D t , el faltante está dado por Ft = D T - V T . En caso contrario el faltante es cero (F T =0). Por lo tanto, se tiene que:
y que
con
Como el pagador de la obligación debe cubrir con sus propios recursos el posible faltante o bien quedarse con el posible excedente, entonces se tiene una opción call en posición larga y una opción put en posición corta, ambas sin costo con subyacente V t y precio de ejercicio D t . Un ejercicio similar al expuesto lo desarrolla Neftci (2008), creando una opción put en posición larga a partir de una call larga y una venta en corto del activo subyacente.
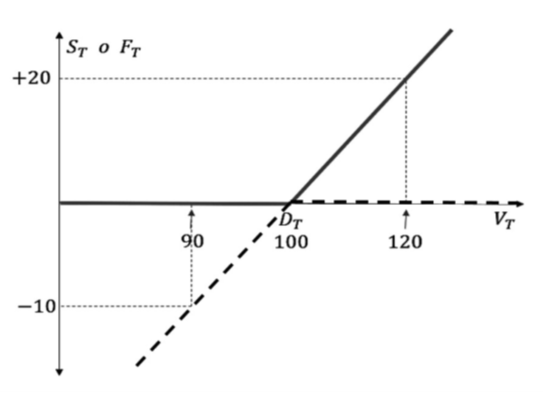
Fuente: Elaboración propia, R-Project
Figura 1 Superávit o déficit de una renta vitalicia para un pagador de pensiones y su descomposición como una opción call en posición larga y una opción put en posición corta.
Por lo tanto, el valor del portafolio de opciones en el tiempo t satisface la condición de paridad put-call:
La ganancia obtenida es la diferencia entre V t y el pago D T a realizar, descontado a una tasa de rentabilidad igual al parámetro de tendencia de la EDE que describe el cambio en V t .
Valuación de S t a partir de un modelo de riesgo de crédito
Siguiendo a Merton (1974), citado por Venegas (2008), es posible calcular la probabilidad de incumplir total o parcialmente con el pago D T , con base en la siguiente deducción, se sabe que S T =max(V T - D T , 0), entonces:
donde
En este caso la probabilidad de que no haya incumplimiento en el pago futuro D
T
, dado el valor actual de la reserva para dicho pago V
T
es
Déficits de reserva y una cobertura dinámica
Para determinar el monto de la reserva constituida debe considerarse a la obligación como la combinación de una opción call en posición larga con una put en posición corta. En ese sentido, una cobertura dinámica implica encontrar un portafolio óptimo en el cual el riesgo de mercado sea eliminado cuando V T < D T . Se considera el portafolio ∏t conformado por w 1 unidades de posiciones cortas en la reserva v t y w 2 y opciones put (F T ) en posición corta.
El cambio en el valor del portafolio está dado por
el Lema de Itô proporciona la EDE que describe el cambio en F T .
reemplazando dV
t
y dF
t
en
Para eliminar el riesgo de mercado, si se hace w
2=1, es necesario que
por lo tanto,
Es decir, por cada opción put en posición corta contenida en el portafolio (o en forma equivalente, por cada obligación de pagar D T en el tiempo T), en el instante t se debe tener en posición corta un porcentaje sobre la reserva V t igual a 1-Φ(d 1,t). De no ser posible tal posición, se utiliza un activo Z tal que Corr(V t , Z t ) ≈ 1. La estrategia anterior constituye una cobertura delta para una opción put en posición corta.
El riesgo que se asume en una sucesión de pagos D T , con T=1,2,3,…,n, es equivalente a tener un portafolio conformado por opciones call en posición larga sin costo alguno, cuya valuación individual viene dada simultáneamente por las siguientes dos ecuaciones, ya expuestas en las secciones 2.2 y 2.3 respectivamente (ecuaciones 16 y 28)
y
de lo anterior se deduce que
el valor esperado condicional de la reserva para el vencimiento , viene dado por:
Valoración de un bono (Cox-Ingersoll-Ross)
Suponga que la tasa de interés de la economía sigue un proceso de la forma:
Entonces, el precio de un bono cupón cero viene determinado por el siguiente conjunto de ecuaciones propuesto por Cox, Ingersoll & Ross (1985b).
Dado que la cobertura dinámica propuesta genera excedentes en la reserva constituida (ahorro generado), se propone que estos flujos de efectivo sean valorados mediante el modelo mencionado. Esta valoración permite cuantificar a valor presente estos flujos futuros, permitiendo así, ajustar la reserva actuarial necesaria para soportar el pago de la renta vitalicia.
Ahorro generado
A través de la cobertura dinámica es imposible, en teoría, que la reserva actuarial para el pago sea inferior al mismo, es decir V T < D T ; por lo tanto, en el peor de los casos V T es igual a D T y en el mejor se presenta un sobrante de dinero. El valor de dichos sobrantes en el presente es el ahorro en la reserva actuarial total producto de la cobertura. Este ahorro, denotado Ah, es igual al valor de un bono cuyos cupones corresponden al sobrante en cada periodo. Este valor puede ser estimado mediante el modelo de tasa corta de Cox, Ingersoll, & Ross (1985b), de la Sección 2.4.
Ingresos/Costos asociados a la cobertura dinámica
La cobertura dinámica propuesta, realizada para cada pago, genera en cada transacción un ingreso o un costo derivado de su misma operación. En el tiempo cero (t=0), este ingreso o costo es igual al valor del portafolio en ese mismo momento multiplicado por la cantidad de unidades vendidas del mismo, que en este caso es delta en cero (0), menos el costo asociado a la tasa de interés del crédito. Esto es:
Como
Por otra parte, el ingreso/costo en el momento t es:
como
Por lo tanto, el ingreso/costo en el tiempo T-1 es:
y en el tiempo T:
entonces, el ingreso o costo total es:
En caso de ser negativo el resultado, se entiende que la cobertura genera costo, no ingreso.
Resultados de los casos de estudio
El sistema de pensiones vigente en Colombia, desde 1993 (Ley 100), se genera como una medida para terminar con los múltiples sistemas de pensiones que hasta ese momento existían. Hoy en día, para la mayoría de la población colombiana, coexisten dos regímenes: el Régimen de Ahorro Individual con Solidaridad (RAIS), que es el esquema de las administradoras de fondos de pensiones privadas (AFP) y, el Régimen Solidario de Prima Media con Prestación Definida (RPM), que es operado por la administradora pública de Colpensiones. Sin embargo, aún se pagan rentas vitalicias a personas que cotizaron a otros regímenes, como los ofrecidos por las entidades territoriales (municipios y departamentos), cuyas reservas actuariales no igualan aún los pasivos pensionales de dichas unidades administrativas. Así mismo, en el caso mexicano, el cambio al nuevo sistema de pensiones de la Ley 97, deja al gobierno con un déficit de las pensiones de los trabajadores que se encuentran afiliados con la ley anterior, ya que se trata de un sistema de beneficio definido; por lo tanto, la carga del pago de dichas pensiones correrá a cargo por el gobierno federal.
Por lo anterior, la relevancia del presente artículo, que determina una solución al déficit que podrían tener estas naciones por el pago de sus pensiones.
Fondo de Pensiones de las Entidades Territoriales de Colombia
En Colombia, el Fondo de Pensiones de las Entidades Territoriales (FONPET) es un fondo establecido por el Ministerio de Hacienda y Crédito Público para apoyar el pago de las pensiones de ex empleados de las divisiones territoriales del país. El FONPET se define como “un fondo sin estatus legal administrado por el Ministerio de Hacienda y Crédito Público, que tiene como objetivo recaudar y asignar recursos a las cuentas de las entidades territoriales y administrar los recursos a través de los patrimonios autónomos”, Dirección de Inversiones y Finanzas Públicas (2017). Actualmente, el FONPET administra aproximadamente 16,000 millones de dólares estadounidenses, siendo el fondo más grande y relevante del país. La estabilidad financiera de los departamentos, municipios y otras entidades gubernamentales, depende en gran medida de la correcta administración de ese fondo.
La Figura 2 muestra la evolución del precio de la unidad de FONPET desde el 1 de febrero de 2018 hasta el 31 de enero de 2019. En este período, su rentabilidad anual fue

Fuente: Elaboración propia con datos del FONPET, R-Project
Figura 2 Valor de unidad del FONPET (01/02/2018-31/01/2019)
En esta sección se utilizaron las tablas de mortalidad oficiales para Colombia que se muestran en el Anexo 1 y se considera un hombre de 60 años de edad cuyos pagos mensuales (mesadas pensionales) crecen anualmente el 3.5%, siendo el primer pago anual correspondiente a 7,000 USD; así mismo, se considera a una mujer con exactamente las mismas características. Un cálculo actuarial realizado con la metodología propuesta por Bowers, et al. (1997) arroja un valor de reserva actuarial de 156,467 USD con una tasa de interés técnico del 3.81% nominal anual para el hombre y de 182,484 USD para la mujer.
Asumiendo que la tasa de interés del bono a 10 años, emitido por el Ministerio de Hacienda y Crédito Público de Colombia, sigue un proceso de Cox-Ingersoll-Ross (CIR), se obtiene una estimación de los parámetros. Para ello se utiliza el método del Hessiano, expuesto por Remillard (2016) y la función est.cir de R-project.
Luego de 1,000 iteraciones, se observa que en todos los casos se presenta una disminución en el capital requerido para financiar la renta vitalicia; también se muestra, por sexo, la disminución en la reserva actuarial necesaria por cada iteración realizada. Como se muestra en la Figura 3.

Fuente: Elaboración propia, R-Project
Figura 3 Disminución, por sexo, en la reserva actuarial necesaria por cada iteración (hombres a la izquierda, mujeres a la derecha).
Para el hombre, la menor disminución es de 20.09% y la mayor de 35.11%; para la mujer, la menor es de 22.54% y la mayor es de 36.73%, como se observa en la Tabla 1.
Tabla 1
Mínimo, primer cuartil, mediana, media, tercer cuartil y máximo
del ahorro generado por el modelo propuesto
| Sexo | Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
| Hombre | -0.3511185 | -0.2893935 | -0.2726112 | -0.273163 | -0.2570137 | -0.2009618 |
| Mujer | -0.3672644 | -0.3135634 | -0.2992640 | -0.29937 | -0.2846892 | -0.2253949 |
Fuente: Elaboración propia, R-Project
La disminución promedio es de 27.32% para el hombre, lo cual representa un ahorro de 42,741 USD, pasando de una reserva actuarial de 156,467 USD a una de 113,726 USD. Para la mujer, la disminución promedio es de 29.93%, pasando de una reserva actuarial de 182,484 USD a una de 127,854 USD, lo cual representa un ahorro de 54,630 USD.
En la Figura 4 se muestra el diagrama de caja (boxplot) de la misma variable.
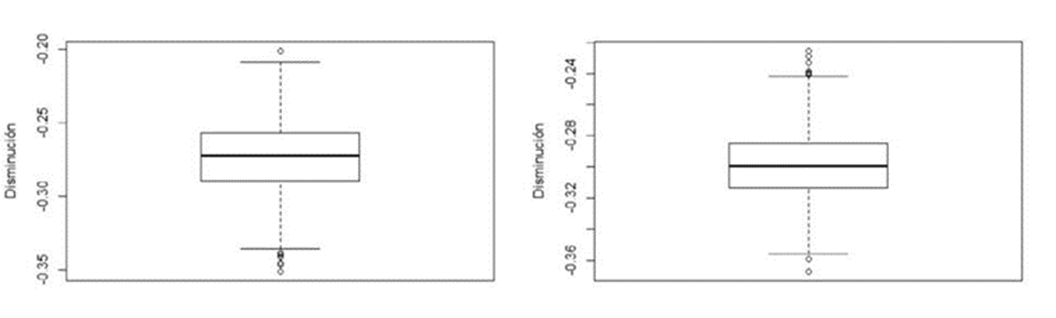
Fuente: Elaboración propia, R-Project
Figura 4 Diagrama de caja de la disminución, por sexo, en la reserva actuarial.
Se puede observar que, las disminuciones en rentabilidad inferiores a 20.84% para hombres y a 24.14% para mujeres, son consideradas datos atípicos superiores. Las superiores a 33.8% para hombres y a 35.69% para mujeres son consideradas datos atípicos inferiores.
En la Figura 5 se muestra el histograma de frecuencias de las disminuciones en las reservas necesarias, tanto para hombres como para mujeres.
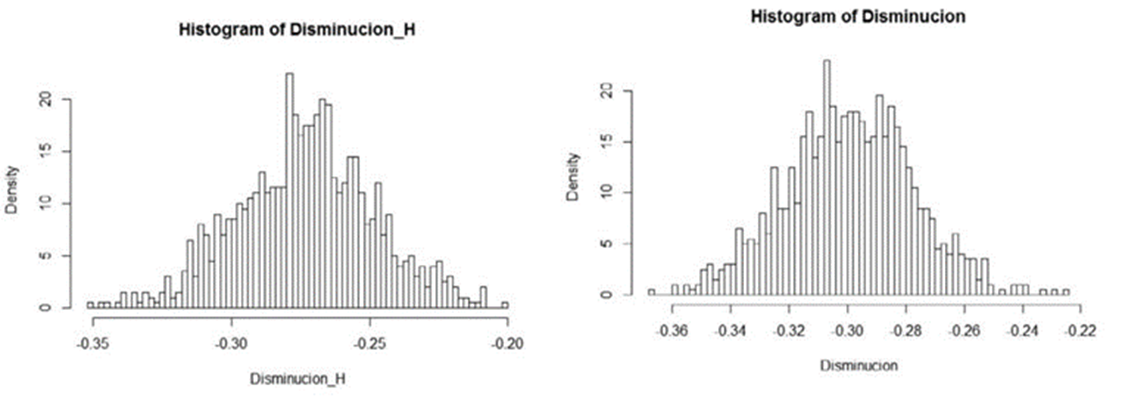
Fuente: Elaboración propia, R-Project
Figura 5 Histograma de frecuencias de las disminuciones por iteración.
A diciembre de 2018 la reserva actuarial de este fondo era de aproximadamente 16,000 millones de dólares estadounidenses y el pasivo pensional a cargo de las entidades territoriales excedía los 22,000 millones de dólares estadounidenses. Asumiendo que los administradores del fondo implementan la estrategia presentada en la presente investigación, se tiene una disminución del 27.32% para hombres y del 29.94% para mujeres (promedio de disminución según los 1,000 escenarios) y que la proporción de hombres y mujeres en la participación del fondo fuera igual a la de la población general (49.37% hombres y 50.63% mujeres), el pasivo pensional sería de 11,417 millones de dólares estadounidenses, lo cual permitiría liberar recursos para cubrir otras necesidades de la población por 4,583 millones de dólares estadounidenses.
Fondos para el retiro de los trabajadores afiliados al IMSS y al ISSTE en México
La Ley del Instituto Mexicano del Seguro Social (IMSS) de 1973 presentaba un esquema de pensiones de beneficio definido, caracterizado por un gobierno que asume el déficit de las cuentas que no logren concentrar la reserva actuarial necesaria para el pago de una renta vitalicia. Luego de más de 20 años, el gobierno mexicano modificó el sistema de pensiones como una medida para incrementar el ahorro interno del país utilizando los fondos de la seguridad social; hasta 1992, el sistema de pensiones para los mexicanos afiliados al IMSS y el Instituto de Seguridad y Servicios Sociales de los Trabajadores del Estado (ISSSTE) se basaba en un esquema de beneficio definido; es decir, sabían de antemano cuánto iban a recibir de pensión de por vida, llegado el momento de la jubilación.
Debido a los cambios demográficos que indican el incremento de la esperanza de vida y la disminución de la tasa de natalidad, aunado a las altas promesas de pensiones y las bajas tasas de contribución de los trabajadores, dichos planes de pensiones no podían ser sostenidos; fue así que el 21 de diciembre de 1995 se publica en el Diario Oficial de la Federación (DOF) la nueva Ley del Seguro Social (Ley), Congreso (1995), con un esquema de contribución definida, en el cual se establece que cada trabajador contará con un fondo en una cuenta individual en una Administradora de Fondos para el Retiro (Afore), por medio de sus Sociedades de Inversión de Fondos de Retiro (Siefore), y que cada trabajador deberá acumular en su cuenta individual durante su vida laboral (hasta los 65 años) la reserva actuarial suficiente para contratar una renta vitalicia con una aseguradora; es decir, los trabajadores gozan de un beneficio equivalente a lo que logren ahorrar. Con esta Ley, existe la posibilidad de que los trabajadores que hayan cotizado 1,250 semanas, no acumulen la cantidad suficiente para dicha contratación de plan de pensión; en este caso, el gobierno mexicano subsidiará una pensión mínima garantizada (un salario mínimo) y los trabajados que quieran gozar de una pensión vitalicia y no cuenten con los recursos necesarios al momento de su jubilación, deberán cargar con el déficit de su cuenta para lograr la compra de su pensión vitalicia.
En la Figura 6 se muestra la evolución del valor de índice de la Siafore Básica 1, portafolio en el cual las Afores, invierten el dinero de las reservas actuariales de las personas mayores de 60 años. Esta información corresponde al periodo comprendido entre el 1 de febrero de 2018 hasta el 31 de enero de 2019. En este período, la rentabilidad anual fue
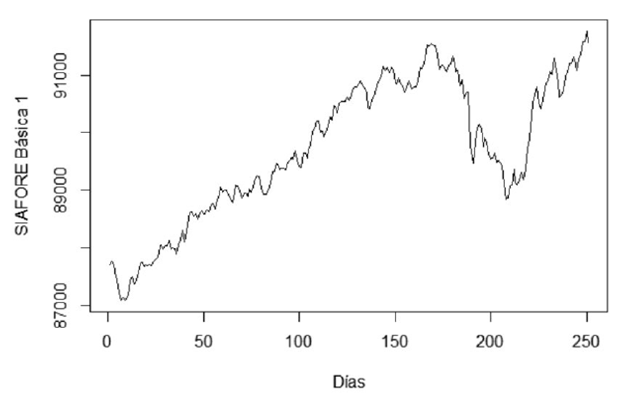
Fuente: Elaboración propia con datos de la CONSAR, R-Project
Figura 6 Valor de índice de la Siefore Básica 1 (01/02/2018-31/01/2019).
En esta sección se utilizaron las tablas de mortalidad oficiales para México que se muestran en el Anexo 2 y se considera un hombre de 60 años de edad cuyos pagos mensuales (mesadas pensionales) crecen anualmente el 3.5%, siendo el primer pago anual correspondiente a 7,000 dólares estadounidenses; así mismo, se considera a una mujer con exactamente las mismas características. El cálculo actuarial tradicional arroja un valor de reserva actuarial de 152,296 dólares estadounidenses para hombres y 174,348 dólares estadounidenses con una tasa de interés técnico del 4.4151% nominal anual. Asumiendo que la tasa de interés del bono a 10 años, emitido por Banco de México, sigue un proceso de Cox-Ingersoll-Ross (CIR), se obtiene una estimación de los parámetros a través del método del Hessiano, Remillard (2013) y de la función est.cir de R-project.
Luego de 1,000 iteraciones se evidencia que en todos los casos se presenta una disminución en el capital requerido para financiar la renta vitalicia (Figura 7). También se muestra la disminución, por sexo, en la reserva actuarial necesaria por cada iteración realizada.

Fuente: Elaboración propia, R-Project
Figura 7 Disminución en la reserva actuarial necesaria por cada iteración por sexo (hombres a la izquierda, mujeres a la derecha)
Para el caso del hombre, la menor disminución es 4% y la mayor es 73.27% ; para el caso de la mujer, la menor disminución es 41.65% y la mayor 91.66%, como se observa en la Tabla 2.
Tabla 2
Mínimo, primer cuartil, mediana, media, tercer cuartil y máximo
del ahorro generado por el modelo propuesto
| Sexo | Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
| Hombre | -0.7327453 | -0.4505040 | -0.3946375 | -0.390327 | -0.3350959 | -0.0399676 |
| Mujer | -0.9165761 | -0.6987917 | -0.6411653 | -0.641158 | -0.5846981 | -0.4165424 |
Fuente: elaboración propia, R-Project
La disminución promedio para hombres es 39.03%, lo cual representa un ahorro de 59,445 dólares estadounidenses, pasando de una reserva actuarial de 152,296 dólares estadounidenses a una de 92,851 USD. Para la mujer, la disminución promedio es de 64.12%, pasando de una reserva de 174,348 dólares estadounidenses a una de 62,564 dólares estadounidenses, lo cual representa una disminución de 111,785 dólares estadounidenses. En la Figura 8 se muestra el diagrama de caja (boxplot) de la misma variable.

Fuente: Elaboración propia, R-Project
Figura 8 Diagrama de caja de la disminución en la reserva actuarial por iteración por sexo (hombres a la izquierda)
Como se observa, disminuciones inferiores a 16.20% y superiores a 62.36% para hombres, son consideradas atípicas. Para mujeres, se consideran atípicas las superiores a 87%. En la Figura 9 se muestra el histograma de frecuencias.

Fuente: Elaboración propia, R-Project
Figura 9 Histograma de frecuencias de las disminuciones por iteración por sexo (hombres a la izquierda, mujeres a la
Según la Comisión Nacional del Sistema de Ahorro para el Retiro, CONSAR (2018), el gasto público comprometido para la Pensión Mínima Garantizada (PMG) alcanza, en valor presente, 43,697 millones de dólares estadounidenses. Asumiendo que los administradores de los fondos de retiro implementan la estrategia, se tiene una disminución en la reserva actuarial necesaria de 39.03% para hombres y de 64.12% para mujeres y que la composición por sexo de los titulares de los derechos pensionales es igual a la composición por sexo de la población general (48.6% hombres y 51.40% mujeres), el pasivo pensional sería de 21,007 millones de dólares estadounidenses, lo cual representaría un ahorro de 22,690 millones de dólares estadounidenses.
Conclusiones
En la presente investigación, se propone un modelo para la estimación del monto de la reserva actuarial de una renta vitalicia a una vida, este planteamiento considera la dinámica estocástica de los activos en los cuales está invertida dicha reserva y por lo tanto del portafolio que soporta la renta. Así mismo, se presenta una estrategia de cobertura dinámica, que a través de una opción put sintética, anula cualquier déficit en la reserva actuarial, haciendo imposible en teoría que el pagador de la renta presente pérdidas. Los excedentes generados son valorados mediante el modelo de Cox, Ingersoll & Ross (1985b) y son restados al cálculo inicial de la reserva necesaria, junto con los costos generados por la cobertura dinámica (o sumados si se trata de ingresos).
El modelo propuesto es aplicado al FONPET en Colombia y a los Fondos para el retiro de los trabajadores afiliados al IMSS y al ISSSTE en México. En el primer caso, la estrategia de gestión del portafolio propuesta podría representar un ahorro en el gasto público de 28.64%, equivalente a 4,583 millones de dólares estadounidenses, aproximadamente. En el caso de México, el ahorro es de 51.92%, equivalente a 22,690 millones de dólares estadounidenses aproximadamente. La relevancia de la estrategia radica en la posibilidad de disminuir el costo de una renta vitalicia, permitiendo una mayor cobertura de los sistemas de retiro, con los beneficios sociales y fiscales que ello implica.











 nueva página del texto (beta)
nueva página del texto (beta)


