1. Introduction
This article introduces a model of political negotiation in order to develop an analysis of the interaction between the mayor and municipal council in a negotiation process in the policy space of a municipality, where the agenda that defines municipal public policies is decided. More importantly, it will analyze how this interaction affects resource distribution in the municipal economy through public policies set by the agenda. The model proposed by this article is one of political negotiation in the context of veto player theory (Tsebelis, 2000; Tsebelis and Alemán, 2005).
More precisely, the proposed model of political negotiation considers a situation in which the mayor, a political patron and a policymaker with private information about his rent-seeking activities, rises to office through vote buying during the electoral campaign. His election also promotes the political organization to which he/she belongs and a cartel of patrons and businesspeople who collude in order to control a significant portion of municipal wealth.
The starting point of the paper is the result established by Cendales (2012) that a political party’s vote buying in elections affects its behavior as the governing party. Cendales (2012) also demonstrated that the mayor’s clientelist rationality is distinguished by selective plundering of the wealth of worse-off individuals, given that this is an effective strategy for manipulating and reproducing electoral capital in the next election in order to co-opt government at the subnational level. Why? Cendales (2012) demonstrated that if the mayor and his or her political organization bought the votes through their political operators in the context of networks, then the mayor wants to impoverish worse-off individuals because their votes will then be cheaper in the following elections. We say that the result established by Cendales (2012) is a parameter of this political negotiation model (See section 1.3).
It should be noted that, given the characteristics of the political organization to which the mayor belongs, the model describes a municipal context in which democracy is precarious, given that the mayor elected to govern is not free from the controls of non-elected individuals/organizations (Bejarano, 2011). The political organization to which the mayor belongs is in charge of determining his or her political agenda. It should be clear that the political negotiation model proposed in this paper does not belong to the set of models that describe full democracies; although this model assumes that elections are democratic, the political organization to which the mayor belongs obtains votes mainly by purchasing them. Thus, democracy exists legally, but in practical terms, democracy is precarious in the sense that political competition is not fully guaranteed (Bejarano, 2011).
Using the governing party’s clientelistic rationality as defined by Cendales (2012), which determines the mayor’s preferences in the policy space, the political negotiation process between the mayor and the municipal council is described as a political negotiation game (PNG) as in Tsebelis (2000) in the context of veto player theory. Why are the mayor and council veto players? Because “...veto players are individual or collective decision makers whose agreement is required for the change of the status quo” (Tsebelis, 2000: 442) and “if the constitution identifies some individual or collective actors that need to agree for a change of the status quo, these obviously are veto players” (Tsebelis, 2000: 446).
Who is on the municipal council? The municipal council is controlled mainly by councilors who promote political agendas with which they seek to increase the amount of public goods and services that better-off persons receive. If better-off persons promote their majority representation in the municipal council then the council will not promote a political agenda that benefits worse-off individuals.
Note that the model proposed here analyzes the logic of negotiation between a mayor and a municipal council during a term of government. Given that a good description is indispensable to evaluating the consequences of any political regime, this model assumes the existence of a precarious democracy at the local level, based on the characteristics of the political organization to which the mayor belongs. It also assumes that the municipal council promotes political agendas that provide better-off persons with greater participation in the public provision of goods and services.
The main result of this article (Proposition 5) demonstrates that the interaction between the mayor and the council has a negative effect on the allocation of resources if the municipal council is non-prioritarian that is, if it approves agendas in which better-off individuals receive higher priority in the execution of public policy. More precisely, we prove that in the political equilibrium, public sector resources that are used to finance policies that benefit worse-off individuals will be plundered in such a manner that the resource distribution of the municipal economy will be, in a stable way, more inequitable. Given that the individual’s endowment of wealth consists of private assets and public sector assets, we assume that the stock of private assets is constant with a depreciation rate equal to zero, and the rate of depreciation of public sector assets is positive.
Thus, if the resources used by the mayor to finance public policies do not remedy the depreciation of public assets, then the stock of wealth of individuals will decrease.
Hence, the negotiation between the mayor and the council induces a political equilibrium in which plundering of public resources by the mayor is maximized, i.e., the mayor’s clientelist rationality is carried out optimally. Thus, the system of ends of a non-prioritarian council is consistent with the system of ends of the mayor who, by controlling the executive apparatus in the municipal political system, installs a predator state.
In this model of political negotiation in an already precarious democracy, this democracy becomes even more precarious such that, as the paper clearly states, the institutional context considered is one in which the mayor is not elected through a competition but is placed in that position by a clientelist organization through vote buying at the local level.
If the institutional context considered in this paper is one in which the mayor obtains his or her position through a clientelist organization that engages in vote buying at the local level, this has two implications. First, the mayor acts under the coercion of groups that have not been elected and do not possess democratic authority. Second, the electoral mass is mobilized through intensive vote buying at the local level: the votes that enable the mayor to win are obtained through economic payments, not through the voters’ thoughtful and critical judgment.
The analysis provided in this article is quite close to that proposed by Bandiera and Levy (2011) in that it considers a type of social situation in which democracy, rather than benefiting worse-off individuals, deteriorates their well-being. However, unlike Bandiera and Levy (2011: 1 322), in our analysis this outcome is not due to diversity of preferences among the poor, but rather to the fact that the governing party, led by the democratically elected mayor, plunders public resources used to finance public policies that favor worse-off individuals in order to worsen the material conditions in which worse-off individuals live, thus reducing the price of votes in the next mayoral election (Cendales, 2012: 254). We say that this is a democracy besieged by a political organization that, having won control of the mayor’s office, seeks to coopt it.
Given the crisis of political representation, the main result established in this article contradicts the implications of both the responsibility hypothesis formulated in economic vote literature (Paldam, 2008: 535) and the median voter hypothesis (Brunner and Ross, 2010: 898). There are two reasons for this. First, in our analysis, the choice of public policies does not depend on the objective of maximizing the preferences of the median-income voter. Rather, this depends on political negotiation processes influenced by veto players, resulting in a political equilibrium in which the demands of worse-off individuals or median-income voters (see Brunner and Ross, 2010: 898) are not represented. Instead, what are represented are the demands of the political organization that is coopting the state at the local level.
Second, in this scenario worse-off individuals do not exact an electoral penalty, given that the votes mobilized by the party during the campaign are bought, rather than ceded spontaneously by citizens, as would be the case if those citizens felt that their needs were addressed by the party’s political platform. Why do worse-off individuals sell their votes? Given the crisis of political representation (Schaffer, 2006), “...the payment obtained by the voter in a vote market, regardless of what it is, will always be greater than nothing, which is precisely what the voter obtains with the public policies that are executed, regardless of which party is governing. This situation is not implausible, as it occurs in certain Colombian territorial entities such as municipalities, departments or towns where vote buying is a practice widely accepted by voters” (Cendales, 2012: 238).
The article is organized as follows. In the preliminaries, we describe a non-prioritarian economy and the policy space. This is followed by definitions of not only the properties exhibited by the council’s and mayor’s preferences in the policy space, to establish something similar to a political configuration at the municipal level, but also the PNG associated with it, which is a dynamic game with complete and perfect information. This is so that, given the order in which the veto players move, we are able to resolve the PNG by applying the backward induction method to find what is known in game theory literature as a subgame perfect Nash equilibrium (SPNE). This equilibrium determines the set of public policies that will be applied in the municipality, in such a manner that the set of public policies being applied in the municipal economy is a political equilibrium or status quo in the policy space (Tsebelis, 2000).
In the Results I section, we study a set of negotiation games, distinguishing two types of political equilibrium in such a manner that both the preferences of the mayor and the council are taken exogenously. In the first type of equilibrium the council is able to impose the continuity of the status quo, even when the mayor sets the agenda, and hence, the political equilibrium is the same status quo. In the second type of equilibrium, if the municipal council offers increasingly lesser priority to the worse-off individuals in the agenda, ceteris paribus, then a greater amount of wealth will be expropriated from those individuals. We emphasize that in each PNG considered in this section, the council’s preferences are taken exogenously.
In the Results II section, the council’s preferences are endogenized through a game, since these preferences depend on an incentives scheme offered by the mayor. We demonstrate that, given the incentives implemented by the mayor, the council adopts preferences in the policy space that induce a political configuration in which the council is indifferent between the agenda that induces the status quo and the mayor’s agenda. This implies that in political equilibrium the mayor will plunder municipal public resources to the extent established by his system of ends, installing a predator state in a precarious municipal democracy. Section 4 presents the related literature.
2. Preliminaries
2.1. A non-prioritarian economy
Two approaches are emphasized. The first is that of the capacities proposed by Moreno-Ternero and Roemer (2006), and which we adopt in our analysis. The second is prioritarianism, proposed both in the context of distributive justice theories of political philosophy and in the context of analytical Marxism (Roemer, 2004). Using both approaches, we will define a non-prioritarian economy.
2.1.1. Capacities
The capacities of an individual are defined as his or her skills at obtaining certain results (income) given the resources he or she has, in such a manner that those results determine the conditions in which the individual lives. Following Moreno-Ternero and Roemer (2006), an individual’s amount of resources is defined as their endowment of wealth.
Given his or her capacities, the individual will produce greater income if his or her endowment of wealth increases, ceteris paribus. We say that an individual has greater capacity with respect to another individual if he or she can generate a greater income with the same endowment of wealth (Moreno-Ternero and Roemer, 2006). Note that an individual’s capacities depend on certain circumstances for which he or she is not responsible, e.g., the cultural, social and economic background of his or her family (García-Pérez and Villar, 2009). In this analysis we assume that an individual’s capacities are exogenous to the model.
There is an income level at which an individual can consume a precise set of primary goods such as housing, education and healthcare, among others, which are “...things that every rational man is presumed to want. These goods normally have a use whatever a person’s rational plan of life” (Rawls, 1971:62).
If an individual, given his or her capacities, produces an income that is less than what is needed to consume the precise set of primary goods, using the minimum endowment of wealth required by any individual to generate an income, then we say that the individual has low capacities. Otherwise, we say that the individual has high capacities. The social group of low-capacity individuals will be denoted as V B and the social group of individuals with high capacities will be denoted as V A . Let us assume that |V B | = |V A | such that |V i | denotes the cardinal of the set V i . Having distinguished between the social groups V B and V A , what does it mean that the economy of a municipality is a non-prioritarian economy?
2.1.2. A non-prioritarian economy
A wealth allocation rule assigns to each individual a certain endowment of wealth, in such a manner that the wealth available in the economy is equal to the sum of the endowments of wealth of all individuals in that economy. An economy is non-prioritarian if the wealth allocation rule provides the lowest endowments of wealth to the voters with the lowest capacities and provides the highest endowments of wealth to voters with the highest capacities, i.e., an economy is non-prioritarian if no priority is offered to individuals who belong to social group V A with respect to individuals who belong to social group in the wealth allocation rule (Roemer, 2004).
The wealth available in the economy is denoted by W ∈ ℝ + such that, given the allocation of wealth in the economy, W i ∈ ℝ + denotes the sum of the endowments of wealth of individuals who belong to social group V i such that i ∈ {A, B}.
Following Moreno-Ternero and Roemer (2006), a municipal economy is defined as a triple (V, u, W) such that V = V
A
∪V
B
is the set of individuals in the economy and
POSTULATE 1. The municipal economy (V, u, W) is a non-prioritarian economy, and hence, W A > W B .
2.2. The policy space
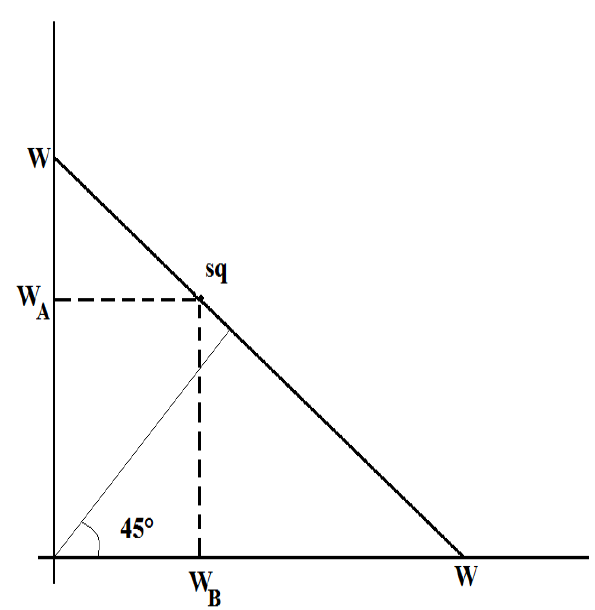
The creation of public policies is the main result of a political system and political actors are precisely those who propose the different public policies that affect the distribution of resources in the economy. Given that public policies influence wealth allocation, let S = {(W B, W A): W B + W A ≤ W} be the set of possible ways in which wealth W can be distributed among social groups V B and V A .
Following Tsebelis (2000), let P ⊂
Therefore, if agenda σ ∈ P is the status quo in the municipality, that is, σ is the set of public policies currently being applied in the municipality, then sq = ψ(σ) ∈ S describes the way in which municipal wealth W is distributed between social groups V B and V A given σ ∈ P. Given that we are considering a non-prioritarian municipal economy (Postulate 1), it holds that the status quo σ ∈ P induces an allocation rule sq = (W B ,W A ) such that W B > W A . Since ψ is a bijective function, we say that sq is the status quo of the municipal political system and S is the policy space (Figure 1).
Assumption 1 says that if two allocation rules are very close, this is because the agendas are very close.
ASSUMPTION 1. The function ψ is an isometry, and hence, ∥σ − σ′∥2 = ∥ψ(σ)−ψ(σ′)∥2 such that ∥·∥2: ℝ m → ℝ is the standard Euclidean norm in m=n,2. Note that if ψ: P→S is an isometry then ψ −1: S → P is an isometry. Henceforth, we suppress the subscript of the function symbol ∥·∥2.
2.3. Veto players
Because of the way in which the municipal political system is organized legally, the veto players are the mayor and the council (Tsebelis, 2000: 442). The political actors are rational in the sense of veto player theory, and in consequence they seek to maximize the realization of their system of ends by choosing certain actions in the policy space. These actions are restricted by the institutions of the political system.
Following Tsebelis (2000), let ≿ i : S → S be a binary relation defined on S such that x ≿ i x′ is read as “allocation rule x is at least as preferred as allocation rule x′”. In particular, there is a wealth allocation rule x i ∈ S that political actor i presumes as optimal given his political rationality and hence, x i ≿ i x for any x ∈ S. It is said that x i ∈ S is the ideal point of political actor i. Following Tsebelis’s approach and given the ideal point x i of the veto player i, we say that this veto player weakly prefers x to x′, if and only if x is closer than x′ to ideal point x i . In symbols, x ≿ i i x′ if and only if ∥x−x i ∥≤∥x′ −x i ∥.
Given that ψ is a bijective function, if x i ∈ S is the ideal point of political actor i, then ψ −1(x i ) = σ i is the ideal agenda of political actor i. Additionally, given Assumption 1, it is possible to define the preferences of political actor i on P based on his or her preferences defined on S. Let ≿ i : P→P be a binary relation on P such that σ ≿ i σ′ is read as “agenda σ is at least as preferred as agenda σ′”. Let us define ≿ i as follows: if ψ(σ) = x and ψ(σ′) = x′ then σ ≿ I σ′ if and only if ∥x − x i ∥≤ ∥x′ − x i ∥. Given that ψ is an isometry, it holds that σ≿ i σ′ if and only if ∥σ − σ i ∥ ≤ ∥σ′ − σ i ∥. Hence, the veto player i weakly prefers σ to σ′, if and only if σ is closer than σ′ to ideal agenda σ i . Note that if ψ (σ) = x and ψ (σ′) = x′ then σ ≿ i σ′ if and only if x ≿ i x′.
On the other hand, the veto player i is indifferent between allocation rules x and x′ if and only if they are the same distance from his ideal point x i . Formally, if ∼ i : S → S is the indifference relation, then x′ ∼ i x if and only if ∥x′ − x i ∥ = ∥x − x i ∥. In consequence, given an allocation rule x different from x i , the set Ii[x] of all allocation rules for which the veto player i is indifferent to x is the set of all rules located in the circle of radius ∥x − x i ∥ = r around the point x i . In symbols, Ii[x] = {x′: ∥x′ − x i ∥ = r}.
Therefore, the veto player’s indifference map is a family of concentric circles around the point x i , such that the indifference curves with smaller radii are strictly preferred to indifference curves with larger radii. In particular, we are interested in indifference curve I i [sq] (Figure 2). We will denote by MI i [sq] the disc of radius ∥sq − x i ∥ around the point x i and hence, MI i [sq] is the set of all allocation rules that the veto player i weakly prefers to the status quo sq.
2.3.1. The Mayor
Given the clientelist rationality of mayor (A), what is the geometric location of his ideal point x A ∈ S in the policy space? Given that one of the mayor’s objectives is to consistently win re-election, in the next electoral campaign he will seek to buy votes in a vote market through his political operators-his clients-thus directly linking his organization to voters.
Whose votes does he buy in the vote market? The votes of worse-off individuals, since the reserve prices for their votes are the lowest in the vote market, given that their demands are low in each possible negotiation with operators. There are two reasons for this (Cendales, 2012).
First, each worse-off individual is willing to sell his vote at a low price because his living conditions are precarious and it is difficult for him to obtain access to primary goods that all individuals need, in order to live in dignified conditions. This is because, given the wealth allocation rule in the economy, this individual’s endowment of wealth is markedly insufficient.
On the other hand, for such voters it is clear that if their desires and needs are not represented politically in public decisions, they must decide whether to sell their vote to a political operator or give it to a candidate whose policy program will never be implemented. The crucial point is that any payment the voter obtains from a political operator for his vote will always be greater than nothing, which is precisely what the voter obtains with the public policies executed by any candidate who wins the election.
The aforementioned is known by the mayor, so that he will seek, during the period in which he governs, to worsen the living conditions of worse-off individuals by executing an inadequate and inefficient investment in public policies that benefit them. This will enable him to negotiate the votes at a lower price in the next electoral campaign, since a reduction in the endowments of wealth of worse-off individuals, ceteris paribus, will induce in them lower valuations of their votes. Therefore, the ideal point x A of the mayor, as an expression of their system of ends, is located in segment [(0,W A ),sq] such that the wealth endowments of social group V A don’t change (see Figures 2a, 2b and 2c).
Note that the mayor’s ideal point x A is a parameter located in segment [(0, W A ), sq]. Why is x A a parameter? Because the preferences of the mayor (or governing party) are not formed in the political negotiation process with the council, the geometric location of the mayor’s ideal point does not depend on that negotiation process.
What does determine the geometric location of the mayor’s ideal point? The geometric location of ideal point x A is determined by the mayor’s objective of selectively looting the wealth endowments of worse-off individuals, given the status quo, as their votes, the cheapest in the vote market, will fall further in price if the mayor loots their wealth endowments.
We say that the geometric location of the mayor’s ideal point x A is determined by his objective in mobilizing the electoral mass needed to win the next election and thus co-opt the mayor’s office. Therefore, it is clear to the mayor not only that his ideal point x A should be located in segment [(0, W A ),sq] given his electoral objective, but more importantly, that his ideal point x A is clearly established before beginning the political negotiation process with the council.
The mayor uses the ideal point x A as a parameter to determine the best bribery strategy for persuading the council in the negotiation process and ensuring approval of his political agenda. If the mayor succeeds in obtaining the council’s approval, he will then be able to mobilize the necessary number of votes to co-opt the mayoralty in the next election.
For the mayor, what is decided in the political negotiation process with the council? This process determines the approval of a specific political agenda that would place the mayor closer to or further from his objective of looting public resources that finance public policies favoring worse-off individuals. Thus, for the mayor, what is endogenous to the political negotiation process with the council is not his ideal point but the approval of a political agenda of equilibrium that will be closer to or further from his ideal point. It is clear that the magnitude of the bribes paid by the mayor to the council in the political negotiation process will determine the proximity of the approved political agenda to his ideal point. How close will this political agenda be to the mayor’s ideal point? This is the critical question to be answered by the model.
2.3.2. The municipal council
The municipal council (C) is a democratic organism responsible for establishing the size of the government and bureaucracy. While the council is a collective veto player, it is assumed to be an individual political actor based on the assumption that there is a political organization that dominates this collective body (Tsebelis, 2000).
What is the geometric location of the council’s ideal point x C ∈ S in the policy space? The council’s ideal point x C is geometrically located in the interval [(0, W), (W, 0)] because the council is not the agenda setter. Moreover, given the norms of the municipal political system, the council only has the capacity to decide whether to accept or veto agenda σ A proposed by the mayor. In consequence, if the council is non-prioritarian, its ideal point x C is located in the interval [(0, W), sq] (see Figures 2a, 2b and 2c).
Note that while the mayor’s preferences in the policy space are one parameter, the council’s preferences in the policy space are endogenous to the model and depend on the incentives scheme offered by the mayor in the negotiation process. This scheme may take the form of bribes and rewards for the municipal council for the magnitude of the resources that can be plundered once the mayor obtains approval of his agenda.
2.4.1. Political configurations
A political configuration in policy space s is a triple (x C , x A , sq), in such a manner that for each political configuration (x C , x A , sq), the sets MI C [sq] and MI A [sq] are well-defined and contain point sq on their borders (see Figures 2a, 2b and 2c).
Figures 2a, 2b and 2c are three possible political configurations in which the positions of the ideal point of the mayor and the status quo do not change. In consequence, if the mayor’s ideal point x A and the status quo sq are parameters in the model, then for each ideal point x C of the council in the interval [e 2 W,sq] there is a political configuration. Therefore, there are as many political configurations as ideal points x C in interval [e 2 W, sq].
Let C (V,u,W)={(x C , x A , sq): x C ∈[e 2 W, sq], x A and sq are fixed} be the set of all possible political configurations that can take place in the non-prioritarian municipal economy (V, u, W) and in which the council is non-prioritarian.
2.4.2. Political negotiation games
For each political configuration (x C , x A , sq) ∈ C (V, u, W) there is a sequential game Γ(x C , x A , sq) with complete and perfect information, such that the set of actions available to veto player i is the disc MI i [sq].
Let W(sq) = MI C [sq] ∩ MI A [sq] be the win-set of game Γ(x C , x A , sq) such that all points in the win-set are accepted by both veto players. In this simplified game the mayor is the agenda setter and the council accepts or rejects the proposal. In consequence, the mayor has significant power to determine the municipal legislative result.
In the first stage of the game, given that the mayor is the agenda setter, he proposes an agenda σ ◦ ∈ P that induces a wealth allocation rule x° = ψ(σ ◦ ) ∈ S. In the second stage of the game, the municipal council must decide whether to accept or veto the agenda σ ◦ ∈ P proposed by the mayor.
If the council accepts the agenda proposed by the mayor, then the payment obtained by veto player i ∈ {A, C} will be as high as political equilibrium x° is close to its ideal point x i , such that if the political equilibrium is its ideal point, then the payment will be infinite. Formally, u i (x°, x°)=1/ ∥ x°− x i ∥if x° ≠ x i and u i (x°, x°) = ∞ if x° = x i . If the council does not accept allocation rule x° then the mayor will have to modify the agenda that he initially proposed. Let {{A, C}, {MI i (sq)} i∈{A,C} , {ui} i∈{A,C} } be the representation in normal form of the dynamic game Γ(x C , x A , sq). We say that (x°, x°) is an SPNE of the game Γ(x C , x A , sq) if and only if x° is a political equilibrium in political configuration (x C , x A , sq) .
3. Results I: A family of political negotiation games in a non-prioritarian economy
We will consider two types of political configurations, in such a manner that in a first political configuration (x C , x A , sq) ∈ C (V, u, W), at the same time that the mayor is a selective predator, the council seeks to preserve the status quo of the municipal political system. In consequence, the council’s agenda σ C is the agenda σ that is currently being applied in the municipal economy, and hence x C = sq.
We note that (sq, x A , sq) ∈ C (V, u, W) is a political configuration in which the set of actions available to the council is a singleton set such that the allocation rule sq is the single element; therefore, the only agenda that both veto players weakly prefer to the status quo is the same status quo (Figure 3a).
What is the political equilibrium that emerges in this political configuration? Proposition 1 answers this question.
PROPOSITION 1. If (x C , x A , sq) is a political configuration in which it holds that x C = sq, then the council has the capacity to impose the continuity of the status quo sq, even when the mayor sets the agenda, i.e., the political equilibrium is the same status quo sq = x C (Tsebelis, 2000; Tsebelis and Alemán, 2005).
Thus, if the municipal council can govern freely with respect to controls, pressures or vetoes exercised by the political organization to which the executive belongs, then the system of brakes and counterweights at the municipal level would impede the executive from having any room to maneuver in terms of negotiating the agenda.
The council has the political capacity to maintain a stable distribution of wealth in a municipality given its capacity to veto any agenda that, having been proposed by the mayor, deviates from the equilibrium agenda. If this is true even when the mayor’s office is controlled by a political organization that seeks to plunder public sector resources used to finance public policies that benefit worse-off individuals, under what conditions is it certain that the mayor has the capacity to selectively expropriate public resources if his political organization’s aim is to co-opt the mayoralty through buying votes in a future election?
To answer this question, we consider a second type of political configuration in which, while the mayor continues to be a selective predator, for the council the optimal extent to which social group V B should be expropriated is positive, and hence, it holds that x C ∈ [e 2 W, sq). However, agenda σ C = ψ −1(x C ) of the council is programmatically more closely identified with agenda σ = ψ −1(sq) than with the mayor’s agenda σ A = ψ −1(x A ); that is, ∥ x C − x A ∥ > ∥ x C − sq∥ (Figure 3b). Note that if ∥ x C − x A ∥ > ∥ x C − sq∥ then x A ∉ MI C (sq), and hence, x A ∉ W(sq).
PROPOSITION 2. If the council is non-prioritarian and its agenda σ
C
is programmatically identified more with agenda σ = ψ
−1(sq) than with the mayor’s agenda σ
A
, that is, ∥ x
C
− x
A
∥ > ∥ x
C
− sq∥, then in the political equilibrium
x° =
With proposition 2 it is possible to state that given that the council is non-prioritarian, in its political negotiation with the mayor it will agree to a certain expropriation of resources that had been allocated to financing public policies that benefit worse-off individuals, if public policies are promoted that favor BO individuals, given the council’s preference for the agenda σ C = ψ −1 (x C ), which is less equitable than agenda σ = ψ −1 (sq) (Figure 3b).
If agenda σ
◦ = ψ
−1(x°), upon defeating agenda σ = ψ
−1 (sq), promotes a more inequitable wealth distribution, then under the hypothesis of proposition 2, what happens to the magnitude of wealth W
B
−
PROPOSITION 3. Under the hypotheses of proposition 2, if the council offers greater priority to BO individuals in the agenda, ceteris paribus, then in the political equilibrium that results from the political negotiation a greater amount of wealth will be expropriated from voting population V B .
Figure 4a shows how what is set forth in proposition 3 corresponds geometrically to establishing that an increment in the magnitude of interval [x C ,sq] implies a reduction in the magnitude of interval [x A , z] given that x° is the political equilibrium described in proposition 2; hence, if the ideological distance between the council’s ideal point x C , and the status quo sq increases, then the council will agree, in its political negotiation with the mayor, to expropriate a greater amount of the wealth received by worse-off individuals. Note that point z is such that interval [ x°,z] is perpendicular to interval [x A − sq] as long as it holds that ∥ x° − z∥ is the distance from point x° to interval [x A − sq]. In symbols,
In addition, note that ideal point x
A
and allocation rule sq are parameters in the analysis and in consequence, political equilibrium
PROPOSITION 4. Let (x C , x A , sq) be a political configuration in which it holds that x A ∈ [e 2 W A , sq) and ∥ x C − x A ∥ = ∥ x C − sq∥. It holds that the mayor is an efficient looter, and in consequence, the political equilibrium x° is x A , and hence, x° = x A .
We say that in each possible political configuration (x C , x A , sq) in which it holds that ∥x C − sq∥> 0, the resources that the mayor effectively is able to loot are “invested” both in the creation of political influence and in maintaining the invisible organizational structure embedded in the political organization (Della Porta, 2004), as these are resources that “... maintain the support of the electoral base in the next election or, at worst, build positions of power that enable them to survive in the future if the next elections are adverse...” (Rehren, 2000: 149).
Given the institutional context considered in the analysis, the council is a collective actor made up of political leaders who as a group can be integrated into a cartel party once they are aware of the incentives they receive from their position in government. Therefore, this article proposes to understand the relationship between the mayor and the council as a relationship between the parties as power networks, in such a manner that they form part of a kind of negotiation and exchange in establishing the agenda that will defeat the status quo.
The magnitude of the resources that the mayor effectively is able to plunder depends on the council’s ideal point position in the policy space, and in addition the mayor knows this. Then, of all the possible political configurations that can take place according to the council’s ideal point, which one emerges from the incentives mechanism surreptitiously implemented by the mayor in the political negotiation process? The following section responds to this question.
4. Results II: The optimal political negotiation game
In this section a game is introduced, in which the council’s ideal point position in the policy space depends on the incentives scheme that the mayor implements in the political negotiation process, and with which the mayor offers a retribution to the council for the magnitude of the resources that he is able to plunder upon approval of his agenda in the negotiation process.
Let x
* be an allocation rule situated on segment [e
2
W, sq] such that ∥x
* − sq∥ = ∥x
* − x
A
∥ (Figure 5a). That is, x
* is an allocation rule with respect to which the council is indifferent between the status quo
sq and the mayor’s ideal point x
A
. Let C(V, u, W) = {(
In particular, if λ = 1 then the council’s ideal point x
C1
is precisely the allocation rule x
*, and therefore in political configuration (x
*, x
A
, sq) the mayor is an efficient predator (proposition 4). On the other hand, if λ = 0, then the council’s ideal point x
C0
is precisely the allocation rule sq, and therefore in political configuration (sq, x
*, sq), the municipal council safeguards the stability of status quo
sq (proposition 1). In consequence, C (V, u, W) is a set of political configurations in which the council’s ideal point
Let Γ(C (V, u, W)) be a sequential game defined over the set of political configurations (C (V, u, W)) such that in the first stage of the game, the council takes an action λ ∈ [0, 1] that will involve a political equilibrium x° in political configuration (x Cλ , x A , sq) in which, by proposition 2, the looting of a certain amount of wealth ∆W B takes place such that |∆W B | ∈ [0, ∥sq − x A ∥] .
Let I ∈ ℝ
+ be the amount of resources from the government budget used to finance public policies whose target population is social group V
B
. Let I: [0,1] → [0,I] ⊂ ℝ be a function such that I(λ) is the amount of resources that the mayor plunders in political equilibrium x° of political configuration (
Note that if the council’s ideal point is
What is the relationship between the amount of wealth ∆W
B
that social group V
B
loses at political equilibrium x° that defeats status quo
sq and the amount of resources I(λ) that the mayor plunders at political equilibrium x° of political configuration (
The larger the quantity of resources plundered from the government’s budget for public policies whose target population is social group V B , the greater the amount of wealth that social group V B loses, given the deterioration of the public sector assets to which it has access. If the physical degradation of such public assets (depreciation) is not reversed, then infrastructure such as schools, health centers, highways, and water, lighting and sewer systems will deteriorate and in some cases may be lost completely.
If φ: [0, I] → [0, ∥sq − x
A
∥] is a function that describes the relationship between the amount of wealth ∆W
B
that social group V
B
loses at political equilibrium x° that defeats status quo
sq and the amount of resources I(λ) that the mayor can plunder at political equilibrium x° of political configuration (
If I(λ) are the resources plundered by the mayor at political equilibrium x° of political configuration (
In the second stage of the game, the mayor observes participations I A (λ) and I C (λ) and chooses bribe C as a reward for the municipal council. The council’s payoff is U(I C (λ)+C) and the mayor’s payoff is V (I A (λ) − C) + k · U(I C (λ) + C), where k > 0 reflects the fact that the governing party, as a cartel party, seeks to include the parties of the council members. In this expression k is the quota of sympathy that the governing party communicates to the parties with seats on the council. It holds that the functions of the mayor’s and council’s payoffs are increasing and strictly concave.
PROPOSITION 5. In the Nash equilibrium of game Γ (C (V, u, W)), the council’s optimal action is λ = 1, i.e., the optimal political configuration is that described in proposition 4.
It can be stated that the council, given its non-prioritarian ideological conception, agrees to choose political agendas that induce openly inequitable allocation rules if there is a mayor whose aim is to loot public resources used to finance public policies benefiting worse-off individuals. The power of the political organization to which the mayor belongs is ratified and strengthened by ensuring the long-term economic well-being of the political structure through looting public resources, since “(...) power is not a free-floating entity, but depends on control of certain strategic resources capital, means of production, organized violence that vary from country to country” (Portes, 2006: 244).
We have demonstrated that a non-prioritarian council, in the context of a municipal political system, legitimizes rather than vetoes the power of a political elite, a dominant class that obtains its power precisely from controlling public resources.
5. Related literature
Orthodox political economy has sought to explain the choice of public policies that make up the status quo in a political system based on the political platforms promoted by the parties and citizens’ preferences for public policies (Roemer, 2001). Furthermore, according to the median voter theory,
“Democracy is generally deemed to be good for the poor; since the elites are few while the poor are many, common wisdom suggests that democracy will lead to the choice of policies that reflect the preferences of the poor” (Bandiera and Levy, 2011: 1322).
However, nothing could be further from Colombia’s political and institutional reality. In many areas of Colombia, whether municipalities or departments, the lower the income of the median voter, the greater the redistributive trend, but of an inequitable nature. Gruner states precisely that
“In particular one observes that fiscal variables such as the size of the redistributive government sector are not related to measures of inequality. According to the data, a given unequal distribution may be politically stable even in presence of large inequalities” (Gruner, 2009:240).
Even so, following orthodox political economy, both Bandiera and Levy (2011) and Gruner (2009) assume that voters expect that the policy announced by the party will be implemented. To cite just one case, Bandiera and Levy (2011) accept that political outcomes in local democracies are determined by the preferences of the median typically poor-agents if there is no diversity in preferences among the poor. However, if there is diversity in preferences among the poor,
“(...) even in fully functioning democracies, where the elites have no additional powers and all votes have equal weight, policy choices may reflect the preference of the elites rather than those of the poor” (Bandiera and Levy, 2011:1322).
Nevertheless, this paper follows the assumption that, while it is certain that the rupture indicated by Gruner (2009) and Bandiera and Levy (2011) exists, this takes place in a party system in which the parties don’t politically represent the needs and desires of voters. In such a context, political consensus among voters is impossible, since the political parties are governed by informal and invisible organizations that selectively represent the needs and desires of their members, rather than members (Freidenberg and Levitsky, 2007). We can say that political economy models produced for developed western economies do not applied to Colombia as long as these models assume that the parties are highly formalized.
In other words, such models simply assume that the parties are organized as set out in their statutes, but these assumptions don’t go far in Latin America. The difference between the way in which parties are organized in their statutes and how they function in practice is enormous (Freidenberg and Levistski, 2007:540).
In the words of Prats (2004:24),
“In Latin America, almost nothing is what it seems, because in many circles institutional informality clearly prevails, sometimes in contradiction to and, in practice, annulling and replacing formal institutions”.
Hence, traditional models are methodologically irrelevant because their analysis omits any description of plotting by the political institutions belonging to such a political system. This plotting determines both the distribution of power among political actors and the nature of the political negotiation process that political actors engage in from their different positions in the policy space and given their relative veto power in the negotiation.
In fact, decisions about municipal public spending -regarding how to determine, distribute and execute the budget to finance such spendingare eminently political, and do not depend, at least in many municipalities in Colombia, on the criteria of rationality that decision models assume to be guiding the behavior of a local government as a decision agent. Rather than obeying criteria of economic efficiency, decisions about public spending instead follow rationality criteria based on certain ideological positions that, situated in the policy space, express the system of ends that formal or informal political organizations seek to promote, consistent with the institutions of a political system and a party system.
In general, the description offered by political competition models of the institutional process in which public policy decisions are made openly neglects the conditions in which a government is situated as a decision-making agent. These institutional conditions make it impossible for the amount and management of public spending to be decided in an independent and unilateral way.
With respect to the relationship between political patronage and wealth distribution, Gallego and Raciborski (2008) consider the patron client relationship in which the client is “free” to decide whether to vote for the political party that has provided him or her with certain favors. They assume that if a party obtains a person’s vote it is because the voter has decided to acknowledge his gratitude for the favors received. Gallego and Raciborski (2008) establish that the electoral quota mobilized by a party is due to the gratitude of those voters who have ceded their vote in response to favors received.
Several considerations with respect to the previous statements: First, Gallego and Raciborski (2008) overlook the fact that a patron uses coercive and violent methods to ensure the client’s adherence, since political patronage is the exercise of a social relationship of domination. Second, patron favors are resources that flow continuously to their clients in order to maintain the political structure of the organization; only a few individuals can be the clients of a patron. Delivering payments to voters for their votes is quite different from granting favors to the patron’s clients, since voters do not belong to the party organization, while clients do.
We can say that the favors that a patron provides to his operator (client) are what link the client to the party organization, such that the patronage organization exists and is administered on
“(...) the basis of asymmetrical transactions, where the former controls the significant resources of power and guarantees, as a ’guardian’, access to them for his clientele in exchange for loyalty and political support. This dyadic relationship is particularist and exists between individuals with unequal power and socioeconomic status with the purpose of obtaining mutual benefits, exchange of jobs, contracts, positions of power and personal links for political support, especially votes” (Rehren, 2000:131).
Therefore, this article provides a rational choice reasoning that sets the first theoretical bases in the context of subnational analysis. These foundations make it possible to establish some statements regarding the relationship between the vote-buying phenomenon, negotiation of the agenda among veto players, and wealth allocation.











 nueva página del texto (beta)
nueva página del texto (beta)