Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Atmósfera
versión impresa ISSN 0187-6236
Atmósfera vol.17 no.2 Ciudad de México abr. 2004
On the multiple-cell thermohaline circulation
S. N. Bulgakov*
Yu. N. Skiba**
*Instituto de Astronomía y Meteorología, Universidad de Guadalajara
Av. Vallarta 2602, Sector Juárez, C.P. 44130, Guadalajara, Jalisco, México
Corresponding author
E-mail: sbulgako@cencar.udg.mx
**Centro de Ciencias de la Atmósfera, UNAM
Circuito Exterior, Ciudad Universitaria, C.P. 04510, México DF, México
Received: September 8, 2003
Accepted: February 4, 2004
RESUMEN
El modelo clásico de circulación termohalina de Stommel (1961) predice la existencia de dos modos de movi-miento del océano para un sistema polo-ecuador: el modo térmico de una celda y el modo halino de una celda. En contraste, los experimentos de laboratorio realizados recientemente con el fin de reproducir este modelo conceptual dan tres estados estacionarios en el espacio de control de los parámetros del modelo: el modo térmico en dos capas, el modo halino en dos capas y un estado híbrido de tres capas. Se aplicó un modelo teórico bidimensional para investigar la formación de celdas múltiples. La solución del orden más bajo analizada usando el método de expansión sugiere la razón de aspecto como un parámetro pequeño. Se demuestra que una asimetría en la distribución vertical de la temperatura y la salinidad es responsable de la formación de una circulación termohalina con celdas múltiples.
ABSTRACT
The classic Stommel (1961) model of thermohaline circulation has predicted the existence of two modes of ocean motion for the pole-equator system. These are, one-cell thermal and one-cell saline modes. In contrast, the laboratory experiments conducted recently to duplicate this conceptual model have found three steady states in the control space of the model parameters: a two-layer thermal mode, a two-layer saline mode, and a three-layer hybrid state. A two-dimensional theoretical model is applied to investigate the multiple-cell formation. The lowest order solution is analysed using an expansion method and suggesting the aspect ratio as a small parameter. It is shown that asymmetry of vertical distribution between temperature and salinity is responsible for forming the multiple-cell thermohaline circulation.
Key words: Thermohaline circulation, theoretical and laboratory modelling
1. Introduction
In the famous Stommel's model (Stommel, 1961) two steady states of thermohaline circulation (THC) were predicted for the pole-equator system. One state is characterised by dominating the temperature for the density difference and creating one cell of water movement with water rising at the equator and sinking at the pole (T-mode). The second one (S-mode), is dominated by the salinity force, providing one cell characterised by opposing vertical circulation.
Further theoretical studies of this problem, including the box models (Rooth, 1982), the 2-D theoretical (Marotzke et al., 1988), global oceanic general circulation (Bryan, 1986) and coupled ocean-atmosphere (Manabe and Stouffer, 1988) models, have confirmed the existence of two principal modes of THC. The third steady state (as pole-to-pole asymmetric one-cell circulation) was found for the pole-equator-pole system (see reviews by Welander, 1986; Marotzke, 1993; Whitehead, 1995; Dijkstra, 2001). Various transient states of THC were noted in the numerical calculations. In particular, a multiple-cell circulation was achieved during the cycle of flow oscillations in the numerical calculations by Quon and Ghil (1995) with the imposed non-monotonic (asymmetric) boundary conditions.
Laboratory studies of the doubly driven flows of THC were recently carried out by Whitehead et al. (2003), Bulgakov and Skiba (2003). Various experimental apparatus were applied to duplicate the conceptual Stommel's box model. The primary finding was that these experiments have not only produced an anticipated two-layer circulation typical for the one-cell modes of THC. In addition, the laboratory runs have revealed an existence of a steady 3-layer flow system, so-called hybrid (H3) states. That is, two-cell circulation was achieved (Fig. 1) for the surface and bottom forcing experiments in the control space of the salt-to-heat buoyancy ratio  and height-to-length aspect ratio
and height-to-length aspect ratio  .
.
Presently, we have applied the 2-dimensional theoretical model proposed by Cessi and Young (1992) to give an interpretation of these phenomena as observed in the laboratory runs.
2. 2-D formulation
The two-dimensional formulation of the problem of the zonally averaged meridional circulation driven by thermohaline forcing was done by Cessi and Young (1992) in dimensionless form as:
 ...............................(1)
...............................(1)
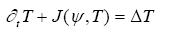 ..................................................................(2)
..................................................................(2)
 ............................................................(3)
............................................................(3)
where 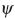 is stream function
is stream function  , Tis temperature, Sis salinity,
, Tis temperature, Sis salinity,  is the Prandtl number,
is the Prandtl number,  is the Lewis number or diffusivity ratio,
is the Lewis number or diffusivity ratio,  is the heightto-length aspect ratio or wave number,
is the heightto-length aspect ratio or wave number,  is the Laplacian operator,
is the Laplacian operator,  is kinematic viscosity,
is kinematic viscosity,  and
and  are the coefficients of heat and salt diffusivities respectively.
are the coefficients of heat and salt diffusivities respectively.
Forcing in a rectangular ocean basin  is provided by the mixed boundary conditions for temperature and salinity, specifying the temperature and the salinity flux at the ocean surface. At the bottom and on the sides of the ocean both the temperature and salinity fluxes vanish, as follows:
is provided by the mixed boundary conditions for temperature and salinity, specifying the temperature and the salinity flux at the ocean surface. At the bottom and on the sides of the ocean both the temperature and salinity fluxes vanish, as follows:
 .................................(4)
.................................(4)
 ....................................................(5)
....................................................(5)
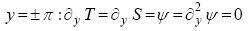 ..................................................(6)
..................................................(6)
The non-homogeneous boundary conditions imposed at the surface for the temperature and salinity fields are supposed to be in equatorially symmetric form proposed by Thual and McWilliams (1992). Because mechanical forcing has been neglected, the boundary conditions for the stream function are homogeneous at all boundaries.
Thus, the problem contains five dimensionless parameters:  and
and  . Here,
. Here,  and
and  are parameters characterising the magnitudes of the temperature and salt flux forcing related as
are parameters characterising the magnitudes of the temperature and salt flux forcing related as  . In such a case the temperature and salinity contribution to the density field should be of the same order (
. In such a case the temperature and salinity contribution to the density field should be of the same order ( , see below the Results section) in contrast to Cessi and Young (1992) suggesting that it should be when
, see below the Results section) in contrast to Cessi and Young (1992) suggesting that it should be when  .
.
The solvability of the problem (l)-(6) was investigated by Cessi and Young (1992). It was noted that this problem could be examined analytically using the expansion method for all the variables and suggesting e as a small parameter.
Collecting terms of the same order, the following lowest order problem could be determined:
 .................................................................................(7)
.................................................................................(7)
 ..................................................................................(8)
..................................................................................(8)
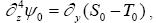 ..................................................................(9)
..................................................................(9)
 ...................................(10)
...................................(10)
 .............................................(11)
.............................................(11)
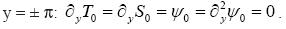 ........................................(12)
........................................(12)
The fixed-temperature boundary condition determines the zero-order temperature while the salinity  is undetermined at this order. The choice of
is undetermined at this order. The choice of  can be argued by saying that temperature diffusion is faster, and salinity evolution is started just in the third order problem. Then, the corresponding zero-order solution can be expressed analytically:
can be argued by saying that temperature diffusion is faster, and salinity evolution is started just in the third order problem. Then, the corresponding zero-order solution can be expressed analytically:
 .....................................(13)
.....................................(13)
where
 .........................................................(14)
.........................................................(14)
The first order problem
 ...............................................(15)
...............................................(15)
 .......................................................(16)
.......................................................(16)
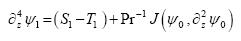 .................................................(17)
.................................................(17)
has the zero conditions at all the boundaries
 .............................................(18)
.............................................(18)
 ...........................................(19)
...........................................(19)
 ......................................(20)
......................................(20)
and its solution is searched as
 ........................................................(21)
........................................................(21)
where
 ...........................................(22)
...........................................(22)
The salinity field  is undetermined as well, and
is undetermined as well, and
 ..........................................................(23)
..........................................................(23)
where
 ...........(24)
...........(24)
The second order problem
 .....................................................(25)
.....................................................(25)
 ....................................(26)
....................................(26)

 .......................................................................................(27)
.......................................................................................(27)
allows further analytical progress for the small amplitudes of external forcing parameters  by neglecting the non-linear advection terms in equations (25) and (27). This problem with the boundary conditions (where non-zero salt flux appears)
by neglecting the non-linear advection terms in equations (25) and (27). This problem with the boundary conditions (where non-zero salt flux appears)
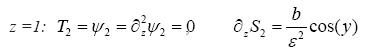 .................................................(28)
.................................................(28)
 ...................................................................(29)
...................................................................(29)
 ..............................................................(30)
..............................................................(30)
has the following diffusion dominated solution
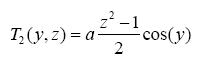 ..................................................................................(31)
..................................................................................(31)
 ....................................................................................(32)
....................................................................................(32)
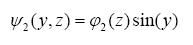 ......................................................................................(33)
......................................................................................(33)
where
 .........................................................(34)
.........................................................(34)
3. Results
Contours of the temperature  and salinity
and salinity  are displayed in Figure 2 forthe equal external forcing parameters
are displayed in Figure 2 forthe equal external forcing parameters  . Here we have chosen
. Here we have chosen  to match the laboratory conditions. As the 1-order solution for temperature is negligible in comparison with the other two terms for the diffusion dominated regime, the shape functions for the temperature and salinity could be expressed as
to match the laboratory conditions. As the 1-order solution for temperature is negligible in comparison with the other two terms for the diffusion dominated regime, the shape functions for the temperature and salinity could be expressed as  and
and  respectively. Their vertical structures are visible in Figure 3 (curves 1 and 2). In this case, temperature effect evidently dominates over the salinity flux through all the depths.
respectively. Their vertical structures are visible in Figure 3 (curves 1 and 2). In this case, temperature effect evidently dominates over the salinity flux through all the depths.
When the solution for salt is changed by a factor of 6 (curve 3 in Fig. 3), i.e.  , this produces a two-cell flow in the vertical direction with the salinity driven motion near the surface, and with the thermal cell of circulation near the bottom. The stream function
, this produces a two-cell flow in the vertical direction with the salinity driven motion near the surface, and with the thermal cell of circulation near the bottom. The stream function  distribution as multiple-cell circulation is shown in Figure 4 when
distribution as multiple-cell circulation is shown in Figure 4 when  and
and  . The latter case (
. The latter case ( ) corresponds to real sea water condition and reflects well an inclination of the zero-circulation line observed in the laboratory experiments under the surface forcing (Fig. la).
) corresponds to real sea water condition and reflects well an inclination of the zero-circulation line observed in the laboratory experiments under the surface forcing (Fig. la).
Solution of the problem for the bottom forcing could be obtained in a similar manner. It is evident that in such a case two-cell circulation is opposite to the flow patterns under the surface forcing. That is, the salinity driven circulation is achieved near the bottom, whereas the thermally driven motion prevails in the upper semiplane (for comparison see Fig. lb).
The interval of the multiple cell circulation  , for both solutions under the surface and bottom forcing, is close to that observed in the laboratory conditions (Bulgakov and Skiba, 2003). As is visible from Figure 5, the lower
, for both solutions under the surface and bottom forcing, is close to that observed in the laboratory conditions (Bulgakov and Skiba, 2003). As is visible from Figure 5, the lower  and higher
and higher  values of the salt flux amplitude produce one-cell thermal and saline circulation correspondingly.
values of the salt flux amplitude produce one-cell thermal and saline circulation correspondingly.
It should be noted that the problem
 ..........................................................(35)
..........................................................(35)
 .................................(36)
.................................(36)
 ......................................................(37)
......................................................(37)
 ...............................................(38)
...............................................(38)
has an analytical solution
 ..........................................................(39)
..........................................................(39)
 ...........................(40)
...........................(40)
Equation (35) differ from (2)-(3) mainly by the absence of Jacobian operators describing differences between the temperature- and salinity-driven circulation. In such a way diffusion of the temperature and salinity is achieved in a similar manner. Thus, the shape functions have the same form. Here the three-layer circulation does not exist, and transitions between T- and S-modes occur directly. This means that asymmetry between the temperature and salinity shape functions (or different ways of temperature and salinity intrusion) is crucial to form the multiple-cell THC.
4. Discussion and conclusions
Two steady states of THC were predicted by Stommel (1961) forthe pole-equator system near the state of equilibrium, which represent one-cell thermal driven and one-cell saline driven water motion.
Quon and Ghil (1995) have paid attention to the multiple-cell formation in their numerical experiments. When they applied non-monotonic (asymmetric about the centre of the pole-equator-pole system) boundary conditions for the temperature and salt flux, the four cells were prominent during the cycle of flow oscillations (see Fig. 8g from Quon and Ghil (1995)).
The laboratory experiments carried out recently (Whitehead et al. 2003; Bulgakov and Skiba, 2003) to duplicate the Stommel's theory have shown that both one- and two-cell THC could be achieved as the steady states. That is, a three-layer current structure was observed in the laboratory runs when the buoyancy ratio was close to a unity  . To give an interpretation of the phenomena observed, we have applied 2-D theoretical model proposed by Cessi and Young (1992).
. To give an interpretation of the phenomena observed, we have applied 2-D theoretical model proposed by Cessi and Young (1992).
In this model, the external forcing for the pole-equator-pole system is provided by the mixed boundary conditions forthe temperature and salinity in equatorially symmetric form. The solution of the problem was analysed with the expansion method by using the aspect ratio ( ) as a small parameter. We assumed that for small amplitudes of the external forcing parameters, diffusion dominates at the lowest-order balance, and the temperature diffusion is faster than the salinity one
) as a small parameter. We assumed that for small amplitudes of the external forcing parameters, diffusion dominates at the lowest-order balance, and the temperature diffusion is faster than the salinity one  . In this case, the problems arising at the three first lower orders could be examined analytically.
. In this case, the problems arising at the three first lower orders could be examined analytically.
The results have shown that these assumptions eliminate the one-to-one correspondence between the temperature and salinity vertical distributions, destroying their symmetry and forming the multiple-cell THC. On the contrary, when temperature and salinity profiles are identical, it is evident that hybrid 3-layer circulation does not exist.
It is well known that the salinity and temperature fields in the ocean are not uniform in the vertical, even to a rough approximation. The different dynamics of the heat and salt transport was documented in the laboratory experiments (Whitehead et al., 2003; Bulgakov and Skiba, 2003) as well. The temperature-salinity symmetry was probably destroyed by the non-monotonic boundary conditions in the numerical experiments by Quon and Ghil (1995) where multiple-cell THC appeared. Therefore, we argue that asymmetry in the vertical distributions of the temperature and salinity is a necessary condition for the multiple-cell phenomena to occur.
Acknowledgments
The study was funded by CONACyT (Mexico) for project 32499-T and by SNI (Mexican System of Investigators) grants 19198 and 14539.
References
Bryan, F, 1986. High-latitude salinity effects and interhemispheric thermohaline circulations. Nature 323,301-304. [ Links ]
Bulgakov, S.N. and Yu.N. Skiba, 2003. Are transitions abrupt in Stommel's thermohaline box model? Atmósfera 16(4), 205-229. [ Links ]
Cessi, P. and W.R. Young, 1992. Multiple equilibria in two-dimensional thermohaline circulation. Journal of Fluid Mechanics 241, 291-309. [ Links ]
Dijkstra, H.A., 2001. Nonlinear physical oceanography: A dynamical systems approach to the large scale ocean circulation and El Niño. Atmospheric and Oceanographic Sciences Library 22, Kluwer, 480 pp. [ Links ]
Manabe, S. and R.J. Stouffer, 1988. Two stable equilibria of a coupled ocean-atmosphere model. Climate Dynamics 1, 841-866. [ Links ]
Marotzke J., P. Welander and J. Willebrandt, 1988. Instability and multiple steady states in a meridional-plan model of the thermohaline circulation. Tellus 40A, 162-172. [ Links ]
Marotzke, J., 1993. Ocean models in climate problems. In: Ocean Processes in Climate Dynamics: Global and Mediterranean examples Malanotte-Rizzoli P. and A.R. Robinson (eds.), Kluwer Academic Publ., pp. 79-109. [ Links ]
Quon, C. and M. Ghil, 1992. Multiple equilibria in thermosolutal convection due to salt-flux boundary conditions. Journal of Fluid Mechanics 245, 449-484. [ Links ]
Quon, C. and M. Ghil, 1995. Multiple equilibria and stable oscillations in thermosolutal convection at small aspect ratio. Journal of Fluid Mechanics 291, 33-56. [ Links ]
Rooth, C, 1982. Hydrology and ocean circulation. Progress in Oceanography 11, 131-149. [ Links ]
Stommel, H., 1961. Thermohaline convection with two stable regimes of flow. Tellus 13(2), 224-230. [ Links ]
Thual, O. and J.C. McWilliams, 1992. The catastrophe structure of thermohaline convection in a two-dimensional fluid model and a comparison with low-order box models. Geophysical and Astrophysical Fluid Dynamics 64, 67-95. [ Links ]
Welander, P., 1986. Thermohaline effects in the ocean circulation and related simple models. In: Large scale transport processes in Oceans and Atmosphere. Willebrand J. and D.L.T. Anderson (eds.), Reidel, pp. 163-200. [ Links ]
Whitehead, J. A., 1995. Thermohaline ocean processes and models. Annual Reviews in Fluid Mechanics 27,89-113. [ Links ]
Whitehead, J. A., M.L. Timmermans, W.G. Lawson, S.N. Bulgakov, A.Z. Martinez, J.M. Almaguer, and J. Salzig, 2003. Laboratory studies of a thermally and/or salinity driven flows with partial mixing. Part 1. Stommel transitions and multiple flow states. Journal of Geophysical Research - Oceans 108(C2), 3036, doi:10.1029/2001JC000902. [ Links ]














